写在前面

今天正式进入前馈神经网络的公式推导环节，综合数据处理难度和公式推导难度以及神经网络的易理解性，我将之前放出的神经网络做了一些调整，之后给出。那么这篇文章主要进行神经网络的变量讲解，以及公式分析。

神经网络图

神经网络图如下所示：

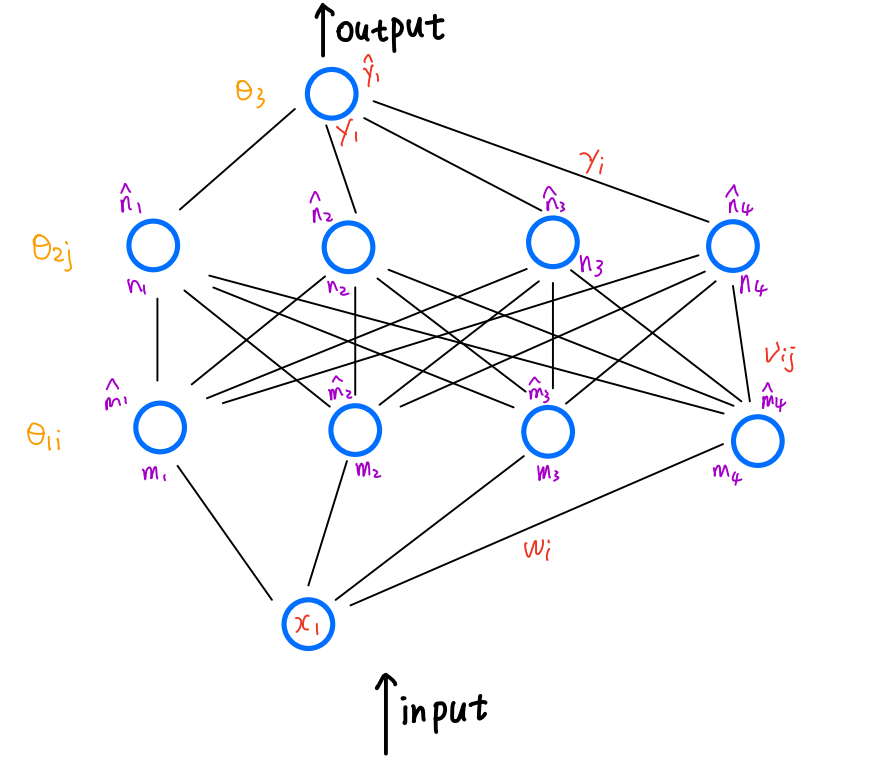
相比于之前的神经网络，我将其修正为了只有一个输入神经元，我将28X28的图像矩阵转换成了784个数据的一维向量，因此我构思的神经网络就是将该一维向量输入神经网络，经过神经网络的处理之后，同样输出784个数据的一维向量。

变量和公式分析

这个神经网络采用的激励函数是sigmoid(x)：

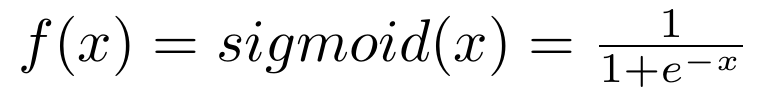
让我们一层层来分析神经网络，首先书输入层到第一个隐层的公式：

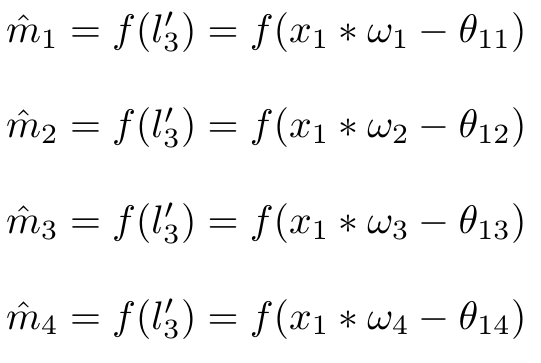
从第一个隐层到第二个隐层的公式：

从第二个隐层到输出层的公式：

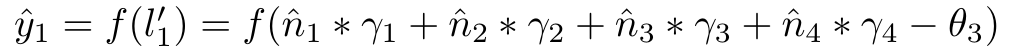
均方误差函数：
均方误差函数前面的1/2是为了在求导时能够将系数消掉，这样使得公式看起来更整洁一些。

写出了各层的公式之后就可以进行梯度下降的公式推导啦，明天更新~

latex公式源码：

\documentclass{article} 
\title{AIplusX} 
\author{AIplusX} 
\begin{document} 
    \ 
    \\$ \hat{y}_{1} = f(l_{1}') = f(\hat{n}_{1} * \gamma_{1} + \hat{n}_{2} * \gamma_{2} +
    \hat{n}_{3} * \gamma_{3} +\hat{n}_{4} * \gamma_{4} - \theta_{3}) $
    \\
    \\ $ \hat{n}_{1} = f(l_{2}')= f(\hat{m}_{1} * \upsilon_{11} + \hat{m}_{2} * \upsilon_{21} +
    \hat{m}_{3} * \upsilon_{31} +\hat{m}_{4} * \upsilon_{41} - \theta_{21}) $
    \\
    \\$ \hat{n}_{2} = f(l_{2}')= f(\hat{m}_{1} * \upsilon_{12} + \hat{m}_{2} * \upsilon_{22} +
    \hat{m}_{3} * \upsilon_{32} +\hat{m}_{4} * \upsilon_{42} - \theta_{22}) $
        \\
    \\$ \hat{n}_{3} = f(l_{2}')= f(\hat{m}_{1} * \upsilon_{13} + \hat{m}_{2} * \upsilon_{23} +
    \hat{m}_{3} * \upsilon_{33} +\hat{m}_{4} * \upsilon_{43} - \theta_{23}) $
        \\
    \\$ \hat{n}_{4} = f(l_{2}')= f(\hat{m}_{1} * \upsilon_{14} + \hat{m}_{2} * \upsilon_{24} +
    \hat{m}_{3} * \upsilon_{34} +\hat{m}_{4} * \upsilon_{44} - \theta_{24}) $
    \\
    \\$ \hat{m}_{1} = f(l_{3}')= f(x_{1} * \omega_{1} - \theta_{11}) $
    \\
    \\$ \hat{m}_{2} = f(l_{3}')= f(x_{1} * \omega_{2} - \theta_{12}) $
    \\
    \\$ \hat{m}_{3} = f(l_{3}')= f(x_{1} * \omega_{3} - \theta_{13}) $
    \\
    \\$ \hat{m}_{4} = f(l_{3}')= f(x_{1} * \omega_{4} - \theta_{14}) $
    \\
    \\$E_{k} = \frac{1}{2} * ( \hat{y}_{1} - y)^{2}$
    \\
    \\$ \frac{\partial E_{k}}{\partial \upsilon_{11}} = \frac{\partial E_{k}}{\partial \hat{y}_{1}} *
        \frac{\partial \hat{y}_{1}}{\partial \hat{n}_{1}} * \frac{\partial \hat{n}_{1}}{\partial \upsilon_{11}} + 
        \frac{\partial E_{k}}{\partial \hat{y}_{2}} *
        \frac{\partial \hat{y}_{2}}{\partial \hat{n}_{2}} * \frac{\partial \hat{n}_{2}}{\partial \upsilon_{11}} + 
        \frac{\partial E_{k}}{\partial \hat{y}_{3}} *
        \frac{\partial \hat{y}_{3}}{\partial \hat{n}_{3}} * \frac{\partial \hat{n}_{3}}{\partial \upsilon_{11}} + 
        \frac{\partial E_{k}}{\partial \hat{y}_{4}} *
        \frac{\partial \hat{y}_{4}}{\partial \hat{n}_{4}} * \frac{\partial \hat{n}_{4}}{\partial \upsilon_{11}}  
        $

\end{document}