很多人都不太清楚机械臂动力学建模的意义，认为其在实际控制过程中意义不大，这种理解层次还是太狭隘了。目前国内很多做机械臂的创业型公司，机械臂产品也就局限在此了，实现了简单了轨迹控制，大部分都停留在通过示教器示教编程轨迹，然后再复现轨迹。这种传统的做法，的确是可以满足目前机械臂市场80%以上的应用场景，但对于复杂的场景，比如力控，牵引示教，高速高精度等场景，仅仅是基于运动学还是无法满足的，此时机械臂的控制也完全被驱动器的自适应控制功能所代替，这也是机械臂动力学建模的意义之所在。

机械臂动力学建模主要是为了获取机械臂运动过程中的关节力矩，有四个目的，其一，将运动过程中的关节力矩通过前馈的方式补偿到驱动器三环控制中的最内环电流环，从而提高驱动器的响应速度进而提高机械臂的高速高精控制；第二，碰撞检测，机械臂在运动过程中，在没有外力时候的关节电流是可以通过实时计算关节力矩近似获得的，一旦驱动器电流环的电流瞬间变大，且远超出近似计算获得的电流值，此时可以判断机械臂发生了碰撞，控制器内部程序可以中断当前规划轨迹的运行。第三，机械臂力控制，通过设定机械臂的末端输出力矩，让机械臂以某一力矩作用在被作用对象上。第四，牵引示教，这是协作型机械臂的必备功能，通过给机械臂施加某一外力，让机械臂沿着外力方向运动。

机械臂的动力学建模目前比较普遍的方法有两种，一种是通过拉格朗日方程进行系统性建模，另一种是通过牛顿欧拉公式进行递推建模，两种方法最终的计算结果一致，但就计算的复杂度而言，关节越多牛顿欧拉方法越具有优势，同时牛顿欧拉递推法在编程实现上也比拉格朗日法更为简单。这里将通过牛顿欧拉递推法对上一章节中的六轴机械臂进行动力学建模。

1.单连杆的牛顿欧拉力学方程

牛顿欧拉方程由两部分组成，牛顿方程用于描述物体的移动时的加速度  和合力  的关系，欧拉方程用于描述物体转动时的角速度  及角加速度  和合力矩  的关系，二者方程表达式如下：

牛顿方程：

欧拉方程：

其中，上式中  ，  ，  ，  ，  均为三维空间中的向量，  为标量。欧拉公式中的  代表物体的惯性矩阵

2.各连杆坐标系位姿

在前面的文章中，介绍了UR构型机械臂的运动学模型，假设采用前面的UR构型机械臂模型参数，对UR构型机械臂进行动力学建模。

则各连杆坐标系相对于前连杆坐标系的位姿矩阵如下所示：

通过将上式中各连杆的位姿矩阵进行位置和姿态分离，可以得到六个连杆坐标系的旋转矩阵  和位置坐标  。

3.各连杆角速度和角加速度

假设某一时刻连杆i坐标系和基坐标系固连，由基坐标系向连杆i坐标系递推连杆i在自身坐标系下的角速度，则有：

将连杆i在基坐标系下的角速度  转换到连杆i自身动坐标系下的角速度：

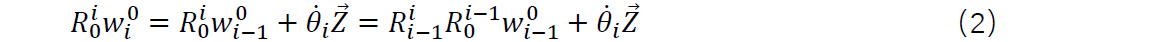
令  ，则有：

上式中，轴向量  0 0 1  , 旋转矩阵 

对公式（3）中的角速度进行求导可以得到各连杆的角加速度为：

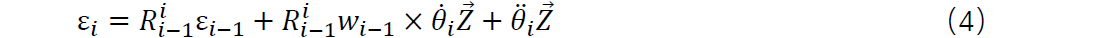
4.各连杆坐标系原点处的线速度和线加速度

假设机械臂正装，也就是机械臂的基坐标系的Z轴方向和重力加速度的方向平行且反向，则基座的加速度为量  0 0 g 。由于某一时刻连杆i坐标系和基坐标系固连，由基坐标系向连杆i坐标系递推连杆i在自身坐标系下的角速度，则有：

将连杆i在基坐标系下的线速度  转换到连杆i自身动坐标系下的线速度：

同样，令  ，则有：

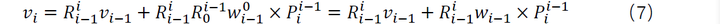
化简上式：

对上式进行求导可以得到：

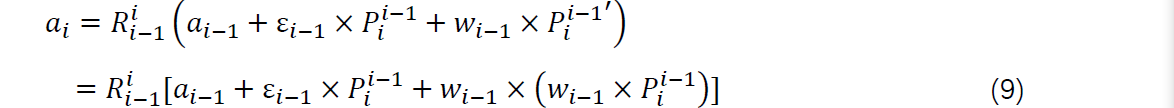
5.各连杆所受合力及合力矩

假设连杆i质心处的加速度为  ，连杆i质心在连杆i坐标系下的位置为，连杆i的质量为，则有：

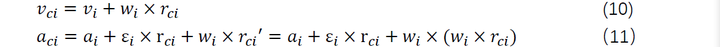
因此，可以得出连杆i的合力为：

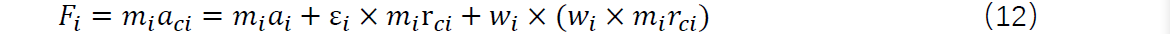
由叉乘公式可以得到：

化简公式（12）可以得到连杆i的合力为：

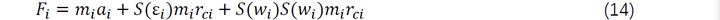
由欧拉方程可以得到连杆i的合力矩为：

注意，上式中合力矩向量是连杆坐标系i下的力矩，连杆i惯性矩阵  不是连杆质心上的惯性矩阵，也是连杆i坐标系下的惯性矩阵。

6.各连杆关节处所受到的力及力矩

将连杆作为受力分析的研究对象，由机械臂末端连杆开始向机械臂基座连杆递推，分析机械臂的各关节受力。

对连杆i列力平衡方程，则其在基坐标下合力  为：

将其转换到自身的动坐标系下：

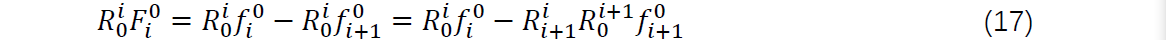
令  ，则有连杆i坐标系下的合力  为：

则连杆i所受外力为：

对连杆i列力矩平衡方程，基坐标系下的合力矩  为：

同样，将转矩从基坐标转换到连杆i自身的动坐标系下：

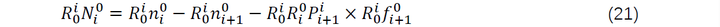
令，，则有连杆i坐标系下的合力矩  为：

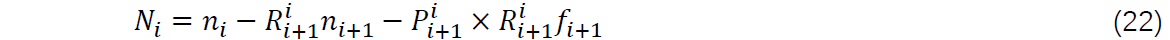
则关节i所受力矩为：

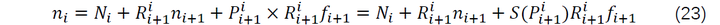
联立公式（14），（19），可以得到：

联立公式（15），（23），可以得到：

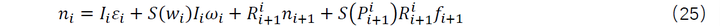
当机器人末端不受外力作用时，

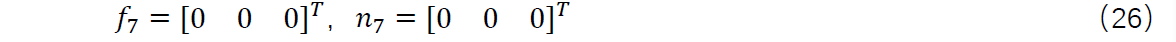
将式（26）代入到（24），（25），可以得到  ，如此反复代入即可求得所有的关节所受到的力和力矩。