逻辑回归可以用来解决分类问题，一个比较经典的例子是猫狗分类 (此例子属于深度学习的范围，因为处理图片需要用到卷积神经网络)。这里将问题简化为二值问题，具体如下图所示。我们需要做的就是找到一条线将这两个标签分开(后面将两个标签用数字  和  表示，即 )。

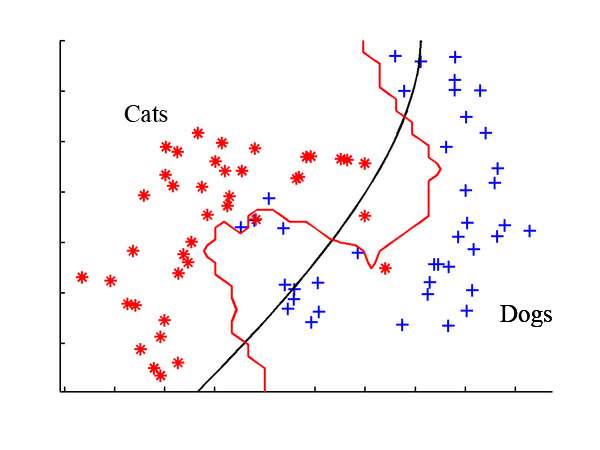
1. 逻辑回归

大多数情况下，按照逻辑回归得出的直线很难将两个标签分清楚：

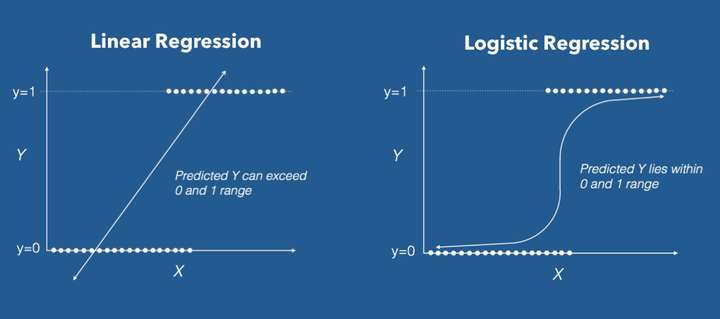
因此这里引入逻辑函数 （Logistic function）。具体的做法是改变假设函数 的形式：

其中有：

此函数被称为双弯曲S型函数（sigmoid function),下图是  的函数图像：

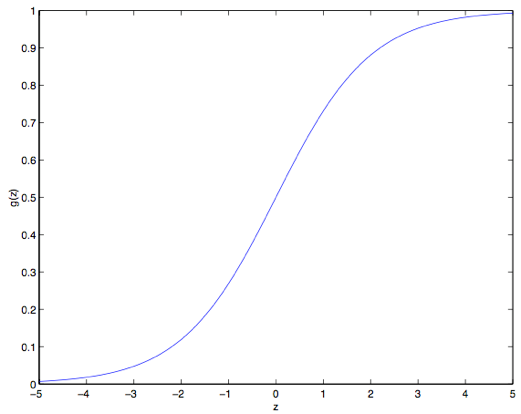
在此曲线中，大于 0.5 的值被认为是 1，小于 0.5 则是 0

之所以选择 sigmoid function 作为逻辑回归函数是因为它有很多便于计算的性质，比如其导数 :

那么，给定了逻辑回归模型了，如何找到最合适的  呢？这里依然使用极大似然法来拟合参数。

首先假设：

更简洁的写法是：

假设  个训练样本都是各自独立生成的，那么就可以按如下的方式来写参数的似然函数：

然后还是跟之前一样，取个对数就更容易计算最大值：

为了使似然函数最大，可以使用类似梯度下降的方法，不过这里是找最大值，所以叫做梯度上升法（gradient ascent）。其公式为：

假设只有一组样本，则该公式的计算结果为：

对于  个样本，则有表达式：

这个表达式看起来与之前线性回归的表达一模一样：

Recap: 线性回归表达式：

其区别是其中 $h_\theta (x) $ 的表达式与线性回归中的不同。

2. 感知器学习算法（The perceptron learning algorithm）

看完上一节的小伙伴可能有个疑问，如果我们至是想让 ，最简单的方法应该是用阈值函数（threshold function）：

依然沿用之前的假设函数 ，便可以得到下面的更新规则：

这被称为感知器学习算法。

这种算法也可以作为分类器使用，但是它只会产生一个线性的分类，对于线附近的样本有分错的可能。即如下图所示：

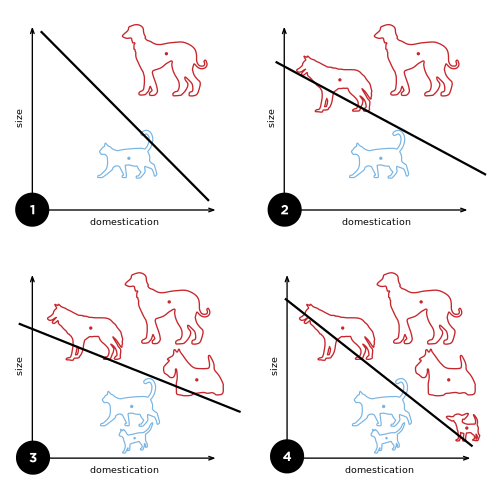
因此现在很少使用这个感知器学习算法了。

3. 牛顿法 (Newton's Method)

之前我们一直使用梯度下降/上升 的方法来计算极大值或者极小值。但其实在 ，其中  较小的情况下，使用牛顿法可以更快速的得到结果。

这里举一个  的例子。对于函数  来说，其极值点的位置即其导数为  的位置：

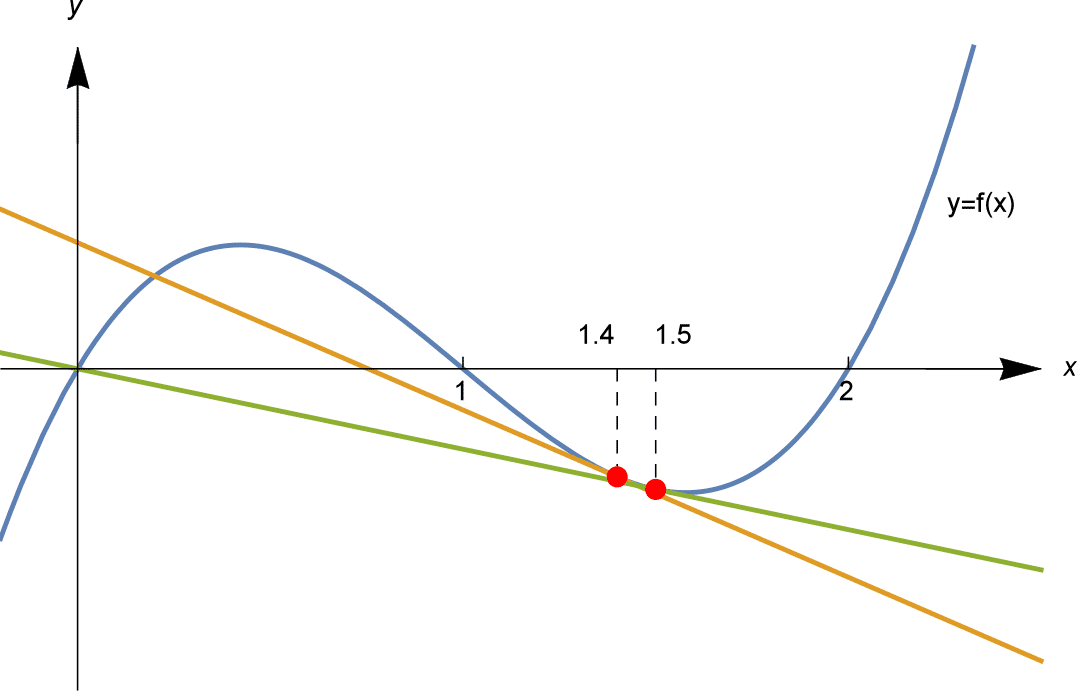
现在使得 ，通过限制的范围，使得 中只包含一个我们想要的极值点。那么要找到  的位置，可以通过求其导数  与  轴的交点来不断的靠近零点。

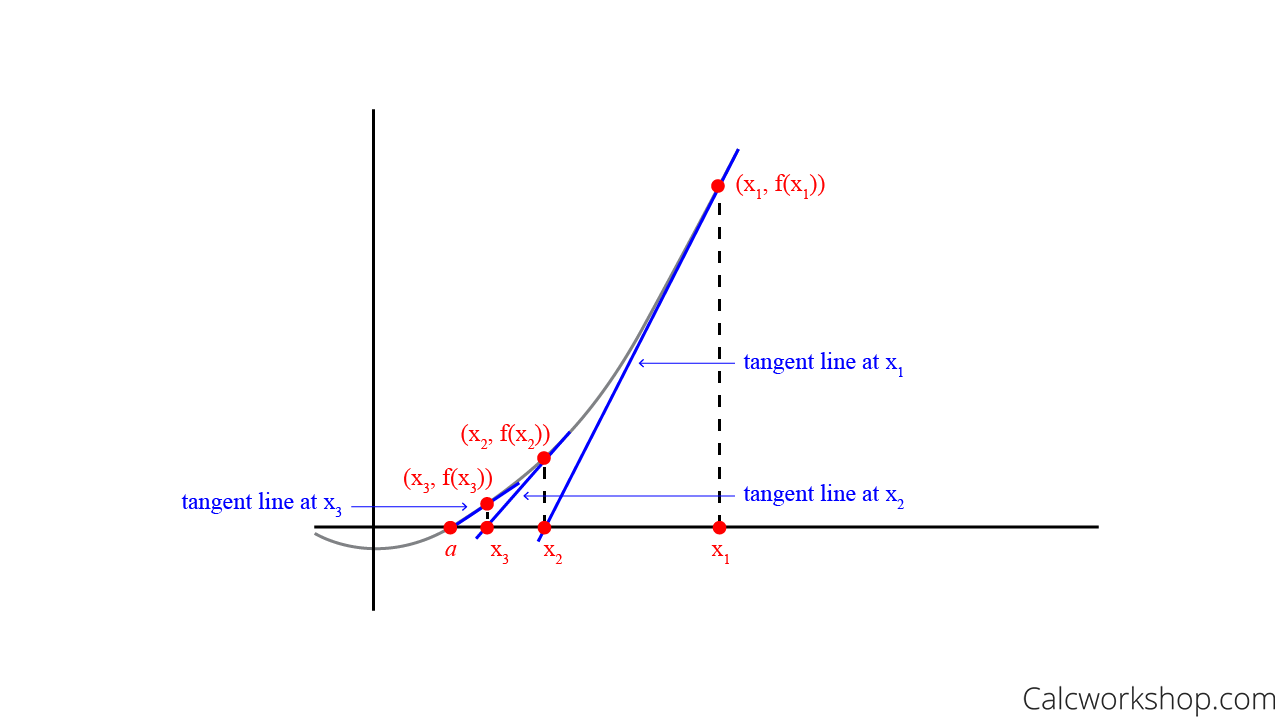
其迭代公式可以表示为：

逻辑回归背景中， 是一个有值的向量，所以我们要对牛顿法进行扩展来适应这个情况。牛顿法进行扩展到多维情况，也叫牛顿-拉普森法（Newton-Raphson method），如下所示：

上面这个式子中的 和之前的样例中的类似，是关于  的  的偏导数向量；而  是一个  矩阵 ,实际上如果包含截距项的话，应该是, ，也叫做 Hessian, 其详细定义是：

牛顿法通常都能比（批量）梯度下降法收敛得更快，而且达到最小值所需要的迭代次数也低很多。然而，牛顿法中的单次迭代往往要比梯度下降法的单步耗费更多的性能开销，因为要查找和转换一个 的 Hessian 矩阵；不过只要这个  不是太大，牛顿法通常就还是更快一些。当用牛顿法来在逻辑回归中求似然函数 的最大值的时候，得到这一结果的方法也叫做Fisher评分（Fisher scoring）。

• 上篇：ML1. 线性回归(Linear Regression) -2
• 下篇：ML3. 广义线性模型(Generalized Linear Models)

本文使用 Zhihu On VSCode 创作并发布