自动驾驶中常见的位姿表示和坐标系问题

敢敢のwings

分类：自动驾驶

个人专栏：机器人基础知识

发布时间 2022.06.20阅读数 4434 评论数 2

0. 简介

在自动驾驶中，我们常常会面对这线性代数位姿表示和坐标系变换问题。之前作者陆陆续续写了一些

1. 线性代数位姿

1.1 矩阵伴随

\begin{aligned} \boldsymbol{R^\mathrm{T}}\exp{(\boldsymbol{p}^\wedge)}\boldsymbol{R} &= \exp{((\boldsymbol{R^\mathrm{T}p})^\wedge)} \\ \Rightarrow\exp{(\boldsymbol{p}^\wedge)}\boldsymbol{R} &= \boldsymbol{R}\exp{((\boldsymbol{R^\mathrm{T}p})^\wedge)} \end{aligned}

1.2 四元数实部和虚部

一个标量和一个矢量来表示四元数就会如下图所示，这样会便于我们计算四元数之间的累乘变换

\begin{aligned} \boldsymbol{q} &= \begin{bmatrix} q_0 & q_1 & q_2 & q_3 \end{bmatrix}^T \\ &= \begin{bmatrix} w & x & y & z \end{bmatrix}^T \\ &= \begin{bmatrix} s & \boldsymbol{v} \end{bmatrix}^T \end{aligned}

连续旋转两个角度可以用这两个旋转对应的四元数的乘积来表示 $\boldsymbol{q}(t_1+t_2) = \boldsymbol{q}(t_1)\boldsymbol{q}(t_2)$

\begin{aligned} \boldsymbol{q}_a \otimes \boldsymbol{q}_b = \boldsymbol{q}(a)\boldsymbol{q}(b) =& \quad\, \ w_aw_b - x_ax_b - y_ay_b - z_az_b \\ &+ (w_ax_b + x_aw_b + y_az_b - z_ay_b)i \\ &+ (w_ay_b - x_az_b + y_aw_b + z_ax_b)j \\ &+ (w_az_b + x_ay_b - y_ax_b + z_aw_b)k \\ =&\begin{bmatrix} s_as_b - \boldsymbol{v}_a^T\boldsymbol{v}_b^T & s_a\boldsymbol{v}_b + s_b\boldsymbol{v}_a + \boldsymbol{v}_a\times \boldsymbol{v}_b \end{bmatrix} \end{aligned}

1.3 四元数与时间

我们说四元数是除了旋转矩阵以外的另一种对旋转表达方式，并且它不具备奇异性，可以表达任意三维旋转，因此有必要学习一下它对时间的求导方式。

$\boldsymbol{u}$ $\theta$ 那这个旋转的对应的四元数可表示为：

\boldsymbol{q} = \begin{bmatrix} \cos{\frac{\theta}{2}} \\ \boldsymbol{u}\sin{\frac{\theta}{2}} \end{bmatrix}

$0$ ，因此上述四元数为：

\begin{aligned} \Delta \boldsymbol{q} &= \begin{bmatrix} \cos{\frac{\theta}{2}} \\ \boldsymbol{u}\sin{\frac{\theta}{2}} \end{bmatrix} \\ &\approx \begin{bmatrix} 1 \\ \boldsymbol{u}\frac{\delta \theta}{2} \end{bmatrix} \\ &= \begin{bmatrix} 1 \\ \frac{1}{2} \delta\boldsymbol{\theta} \end{bmatrix} \end{aligned}

$\delta\boldsymbol{\theta}$ 的方向为旋转轴，模长为（这段时间内非常微小的）旋转角度。

下面对时间求导：

\begin{aligned} \dot{\boldsymbol{q}} &= \lim_{\Delta t \rightarrow 0}\frac{\boldsymbol{q}(t+\Delta{t})- \boldsymbol{q}(t)}{\Delta{t}} \\ &= \lim_{\Delta t \rightarrow 0}\frac{\boldsymbol{q}(t)\otimes\boldsymbol{q}(\Delta{t})- \boldsymbol{q}(t)}{\Delta{t}} \\ &= \lim_{\Delta t \rightarrow 0}\frac{\boldsymbol{q}\otimes\Delta\boldsymbol{q}- \boldsymbol{q}}{\Delta{t}} \\ &= \lim_{\Delta t \rightarrow 0}\frac{\boldsymbol{q}\otimes( \begin{bmatrix} 1 \\ \frac{1}{2}\delta\boldsymbol{\theta} \end{bmatrix} - \begin{bmatrix} 1 \\ \boldsymbol{0} \end{bmatrix})}{\Delta{t}} \\ &= \boldsymbol{q}\otimes\lim_{\Delta t \rightarrow 0}\frac{( \begin{bmatrix} 0 \\ \frac{1}{2}\delta\boldsymbol{\theta} \end{bmatrix} )}{\Delta{t}} \\ &= \boldsymbol{q}\otimes\begin{bmatrix} 0 \\ \frac{1}{2}\boldsymbol{\omega} \end{bmatrix} \end{aligned}

$\boldsymbol{\omega} = \lim_{\Delta t \rightarrow 0}\frac{\delta\boldsymbol{\theta}}{\Delta{t}}$ 是求导时间的角速度。

1.4 旋转矩阵和旋转向量

从旋转向量到旋转矩阵基本就是通过罗德里格斯公式表明：

\boldsymbol{R} = \boldsymbol{\mathrm{\cos{\theta}}I + \mathrm{(1-\cos{\theta})}nn^\mathrm{T} + \mathrm{\sin{\theta}}n^\wedge}

从旋转矩阵到旋转向量的过程可以利用矩阵迹（trace）的性质进行推导：

\begin{aligned} \mathrm{tr}(\boldsymbol{R}) &= \boldsymbol{\mathrm{\cos{\theta}\ tr}(I) + \mathrm{(1-\cos{\theta})\ tr}(nn)^\mathrm{T} + \mathrm{\sin{\theta}}\ n^\wedge} \\ &= 3\cos{\theta} + (1 - \cos{\theta}) \\ &= 1 + 2\cos{\theta} \\ \Rightarrow \theta &= \arccos{\frac{\mathrm{tr}(\boldsymbol{R}) - 1}{2}} \end{aligned}

1.5 李群李代数扰动

$SO(3)$ $(\boldsymbol{\phi}_1, \boldsymbol{\phi}_2)$ 的指数映射时。并且两个李代数其中有一个为小量时，二次项以上的小量都可以忽略。此时， BCH 公式有以下线性形式：

\ln{(\exp(\boldsymbol{\phi}_1^\wedge)\exp{(\boldsymbol{\phi}_2^\wedge))}}^\vee \approx\begin{cases} \boldsymbol{J}_l(\boldsymbol{\phi}_2)^{-1}\boldsymbol{\phi}_1 + \boldsymbol{\phi}_2\qquad \mathrm{当\phi_1 为小量} \\ \boldsymbol{J}_r(\boldsymbol{\phi}_1)^{-1}\boldsymbol{\phi}_2 + \boldsymbol{\phi}_1\qquad \mathrm{当\phi_2 为小量} \end{cases}

$\boldsymbol{R}$ $\Delta\boldsymbol{R}$ 时，BCH 近似过程可以表示为：

\begin{aligned} \exp{(\Delta \boldsymbol{\phi}^\wedge)}\exp{(\boldsymbol{\phi}^\wedge))} &= \exp{((\boldsymbol{\phi}+J_l^{\mathrm{-1}}(\phi)\Delta\phi})^\wedge) \\ \exp{(\Delta \boldsymbol{\phi}^\wedge)}\exp{(\boldsymbol{\phi}^\wedge))} &= \exp{((\boldsymbol{\phi}+J_r^{\mathrm{-1}}(\phi)\Delta\phi})^\wedge) \end{aligned}

$\boldsymbol{\phi}$ $\Delta \boldsymbol{\phi}$ 时，通过 BCH 可以近似为：

\begin{aligned} \exp{(\boldsymbol{(\phi + \Delta\phi)}^\wedge)} &= \exp{\boldsymbol{(J_l\Delta\phi)^\wedge}}\exp{(\boldsymbol{\phi}^\wedge)} \\ &= \exp{(\boldsymbol{\phi}^\wedge)}\exp{\boldsymbol{(J_r\Delta\phi)^\wedge}} \end{aligned}

1.6 李群累加

$\xi$ $a$ 在李群空间附近的邻域上 $\oplus$ 来表示李群的加法，如下所示：

a\oplus \xi \triangleq a \exp{(\hat{\xi})}

$\xi\in\mathbb{R}^n$ $a$ 极小值右乘的做法 $\xi = \omega t$ $a$ 作为参考系下的一个角度扰动；

$\hat{\xi}$ $\xi$ $\xi^{\wedge}$ ；

$\exp{\xi}$ 为李代数到李群的指数映射；

$\hat{\xi} = [\omega t]_{\times}$ $_{\times}$ 来表示角度扰动（旋转轴+旋转角度）的旋转向量。

2. 各种传感器默认坐标系

2.1 摄像头坐标系相机坐标系的方向一般为：X –> 右，Y –> 下，Z –> 前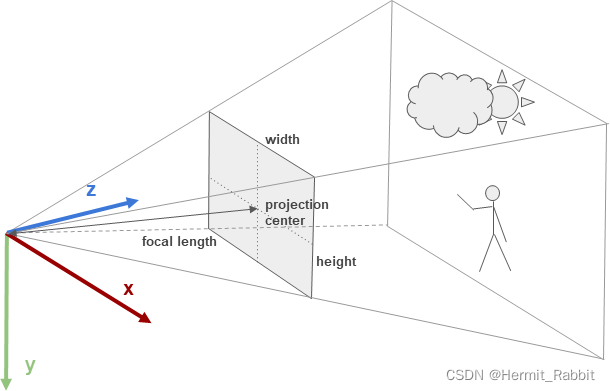

2.2 雷达坐标系

雷达坐标系的方向一般为：Z->上，X->右，Y->前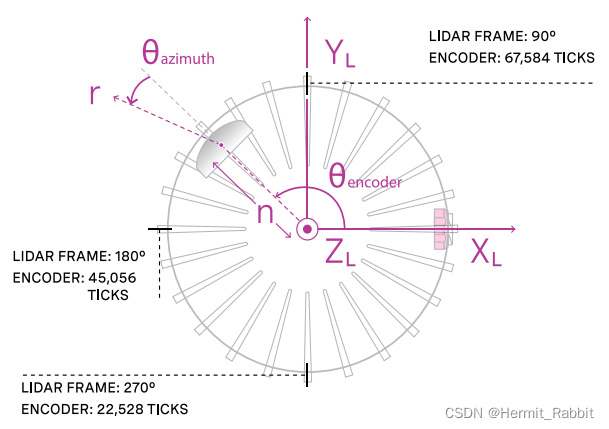在这里插入图片描述

2.3 IMU坐标系

IMU坐标系的方向一般为：Z->下，X->右，Y->后在这里插入图片描述

2.4 GPS坐标系

GPS 自身没有坐标系，一般是由经度和纬度组成。在世界坐标系（WGS84）下的坐标值我们可以通过变换转到本地坐标系，一般会和里程计的坐标系绑定在一起。

2.5 轮速坐标系/车体坐标系

车体坐标系原点在载体质量中心与载体固链，x轴沿载体轴指向右，y轴指向前，z轴和xy满足右手坐标法则指天，又称为右-前-上（r-f-u）坐标系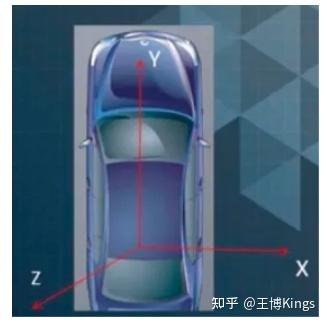在这里插入图片描述

TODO 等看到其他的再更新

3. 参考链接

https://blog.csdn.net/u011754972/article/details/117122975

https://zhuanlan.zhihu.com/p/401812577

https://xiaotaoguo.com/p/mapping_coordinate_systems/

https://www.csdn.net/tags/MtjaggysNzUwODItYmxvZwO0O0OO0O0O.html

https://xiaotaoguo.com/p/robotics_pose_intro/

自动驾驶

原创文章作者：敢敢のwings。如若转载，请注明出处：古月居 http://admin.guyuehome.com/38377

打赏 0

上一篇：C++之中介者(Mediator)模式

下一篇：VSLAM特征之线特征&面特征

自动驾驶中常见的位姿表示和坐标系问题

敢敢のwings

0. 简介

1. 线性代数位姿

1.1 矩阵伴随

1.2 四元数实部和虚部

1.3 四元数与时间

1.4 旋转矩阵和旋转向量

1.5 李群李代数扰动

1.6 李群累加

2. 各种传感器默认坐标系

2.1 摄像头坐标系 相机坐标系的方向一般为：X –> 右，Y –> 下，Z –> 前

2.2 雷达坐标系

2.3 IMU坐标系

2.4 GPS坐标系

2.5 轮速坐标系/车体坐标系

TODO 等看到其他的再更新

3. 参考链接

为你推荐

点云分割路面——GPF算法分析与C++实现

HD-Map lanelet2(2)

Lidar-MOS 安装与使用

笛卡尔坐标系转frenet坐标系

Ubuntu18.04 编译faster-lio，且不升级gcc/g++ 9.0版本（C++17）

精选经典文献阅读之--Traversability Analysis for Autonomous Driving...(Lidar复杂环境中的可通行分析)

评论（2）

关于作者

敢敢のwings

361

2

803

17

精选经典文献阅读之--RigidFusion(动态障碍物SLAM)

经典文献阅读之--BEVDistill(BEV蒸馏)

卡尔曼滤波引出的RTS平滑

相关推荐

精选史上最简SLAM零基础解读(7) - Jacobian matrix(雅可比矩阵) → 理论分析与应用详解(Bundle Adjustment)

自动驾驶之高精地图

基于Open3D的Lidar-Segment

精选C++ 之Google benchmark测试与分析

自动驾驶路径跟踪控制——纯追踪控制

图像处理基础篇-形态学处理-边缘检测(matlab仿真与图像处理系列第4期）

热门泡泡

30积分 失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分 想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

TA的专栏

dlo系列

轨迹规划

大模型

Matlab-ros

深度学习

CUDA

FAST-LIO系列

规范学习

机器人仿真

传感器感知

ROS基础以及进阶

无人驾驶

从零到一的SLAM

机器人基础知识

经典论文阅读

C++模式

专栏导航

给作者打赏

忘记密码

修改头像

添加你感兴趣的标签

举报类型（必选）

举报详情（选填）

2.1 摄像头坐标系相机坐标系的方向一般为：X –> 右，Y –> 下，Z –> 前

30积分失眠，聊聊自己搞ROS的心得体会吧

5积分想买能用ROS2的开发套件。或者开发板