前言

SVM算法在在1995年正式发表，在针对中小型数据规模的分类任务上有着卓越的效果，同时有着完整的理论证明，在20世纪末的几年和21世纪初的10年完胜神经网络，吴恩达在其2003年的《Machien learning》公开课上用两节课的时间对其进行讲解，而神经网络讲解了20min左右。就是这个算法把神经网络按在地上摩擦了大概15年的时间，直到深度学习的兴起。但即便这样，现在SVM算法依旧被广泛的使用。 
SVM大概的可以不确切的分为三个程度理解： 
（1）线性可分情况下的线性分类器，这是最原始的SVM，它最核心的思想就是最大的分类间隔（margin maximization）； 
（2）线性不可分情况下的线性分类器，引入了软间隔（soft margin）的概念； 
（3）线性不可分情况下的非线性分类器，是SVM与核函数（kernel function）的结合。

以上介绍来自：https://blog.csdn.net/chaipp0607/article/details/73662441

相比神经网络，SVM有着完备的数学理论依据，完整学习过SVM的人会觉得它的数学理论非常完美。

SVM的基本型

SVM最大分类间隔的灵感来自于一个非常符合直觉的观察，如果存在两类数据，数据的特征是二维的，那么我们就可以把数据画在一个二维平面上，此时我想找到一个决策面（决策边界）去将这两类数据分开。如下图所示：

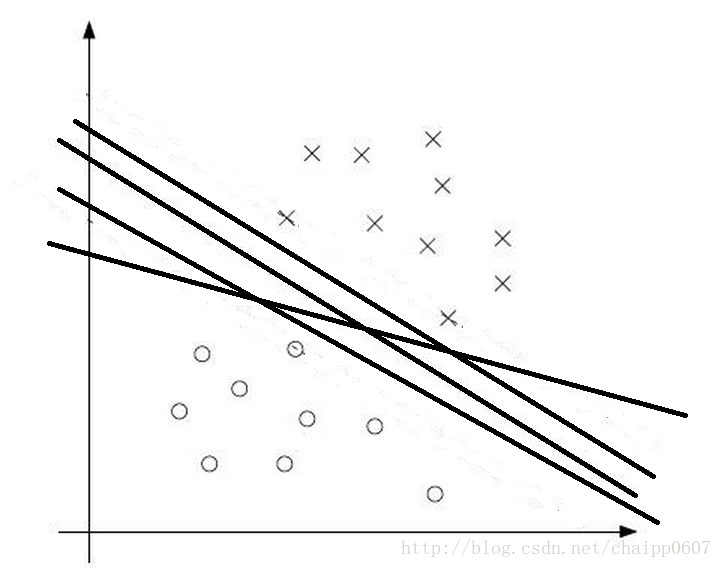
è¿éåå¾çæè¿°

理论上这个决策边界有无数种选择，就像图中画出的四条黑色的线，都能实现分类，但是哪一种是最好的分类方式呢？SVM算法认为在上图中靠近决策平边界的点（正负样本）与决策边界的距离最大时，是最好的分类选择： 

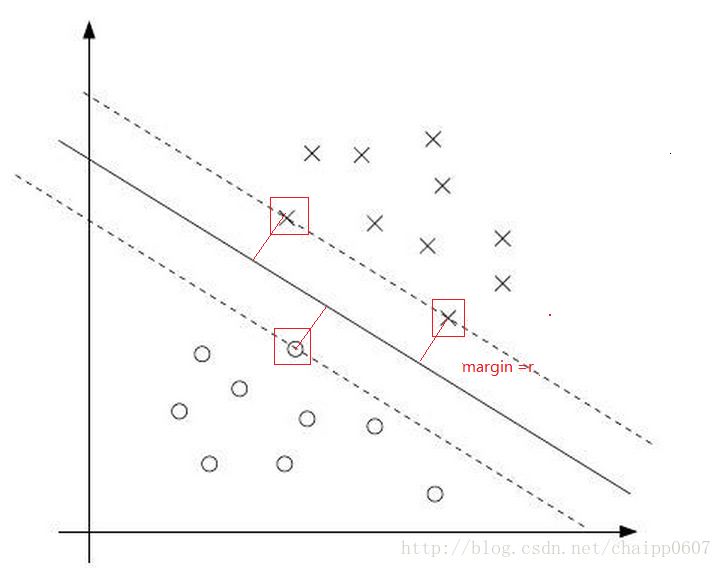
è¿éåå¾çæè¿° 

上图中红色的线就是要优化的目标，它表征了数据到决策边界的距离，这个距离就是所谓的最大分类间隔，也即上图Gap的一半。同时在上面的几个数据，如果靠近两侧的数据少了几个，也不会影响决策边界的确定，而被红色框框出来三个数据才决定了最终的决策边界，所以这三个数据被称之为支持向量。

如何用数学方式表示出最大间隔呢？

首先，样本空间下超平面的线性方程为：

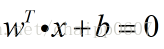
                                        è¿éåå¾çæè¿°

从上面可以看到，此时的支持向量机（没有加核函数）就是个线性的分类器，它的卓越性能就体现在在线性分类器基础上的最大分类间隔。 

所以本质上SVM要训练的参数只有w和b，关键就在于SVM如何在优化中体现最大分类间隔的思想！ 
针对所有的训练数据（traindata），SVM都希望： 

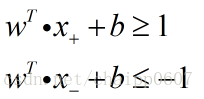
                                                     è¿éåå¾çæè¿°

这里的正负1就体现的最大分类间隔，这里是选择用正负1是为了计算方便，因为无论间隔是多少，都可以依靠伸缩w和b约为1。上述公式就是SVM的最大间隔假设。如下图： 

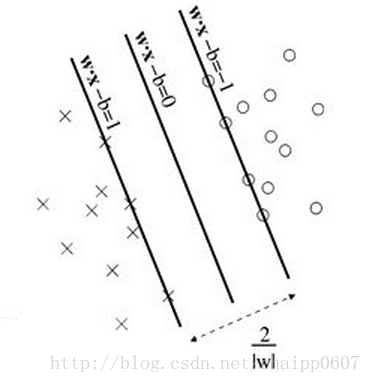
                                                    è¿éåå¾çæè¿°

可已看出，使得 W^{^{T}}\cdot x-b=\pm 1 成立的样本即为支持向量。

已知一个超平面和点x(x1,x2,x3......xn)，那么这个点到这个超平面的距离为：,     向量表示法为。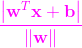

所以支持向量到超平面的距离为  ：

                                                                                 \frac{1}{||W||} 

决策边界两边的线之间的距离（最大间隔）为：    

                                                                                这里写图片描述  

这就是SVM的优化目标，它想要找到其最大值，然后大家可能发现了，这个目标里面没有b，之和w有关，那么是不是任意的b都可以呢？ 
显然不是的，这个优化有一个约束条件，因为推导的过程就有假设条件是几个支持向量要求在超平面两侧，所以这个约束条件可以写成：           

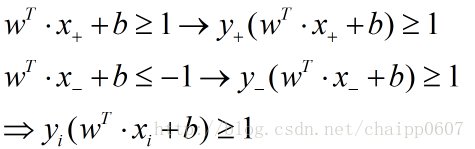
         这里写图片描述

因此，我们最终的目标函数为：

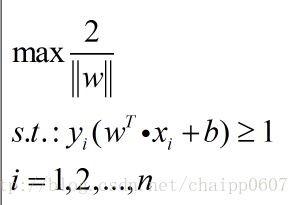
                                                  è¿éåå¾çæè¿°

转化为求最小值问题更加方便：

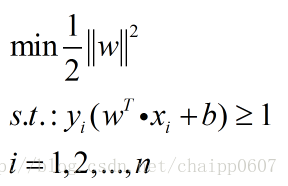
                                                         è¿éåå¾çæè¿°

上式就是SVM的基本型。

SVM中的对偶问题

我们希望求解SVM的基本型来得到最大间隔划分超平面的模型

                                                             f(x)=W^{^{T}}\cdot x-b

模型参数为W,b，也就是要解出W和b。这是一个凸二次规划问题，我们可以用拉格朗日乘子法转化为求和原问题等价的对偶问题，这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题。

根据拉格朗日乘子法：就是求函数f(x1,x2,…)在g(x1,x2,…)=0的约束条件下的极值的方法。其主要思想是将约束条件函数与原函数联系到一起，使能配成与变量数量相等的等式方程，从而求出得到原函数极值的各个变量的解。即可以求得：

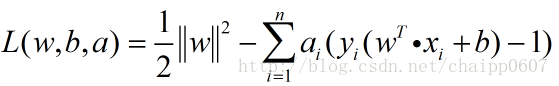
 è¿éåå¾çæè¿°
其中a就是拉格朗日乘子法进入的一个新的参数，也就是拉格朗日乘子。 
那么问题就变成了：

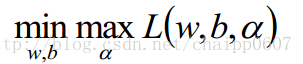
è¿éåå¾çæè¿°

所谓的对偶问题就是：（具有强对偶行，满足KKT条件）

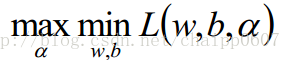
è¿éåå¾çæè¿°

做这种转换是为了后面的求解方便，因为最小值问题，求导就可以啦！！ 
下面对w和b分别求偏导（这里是纯数学计算，直接给结果了）： 

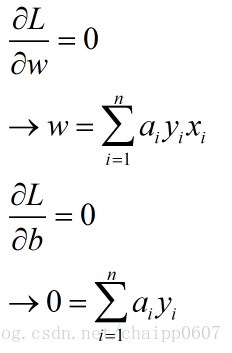
è¿éåå¾çæè¿°

在这里求出了两个结果，带入到L(w,b,a)中：

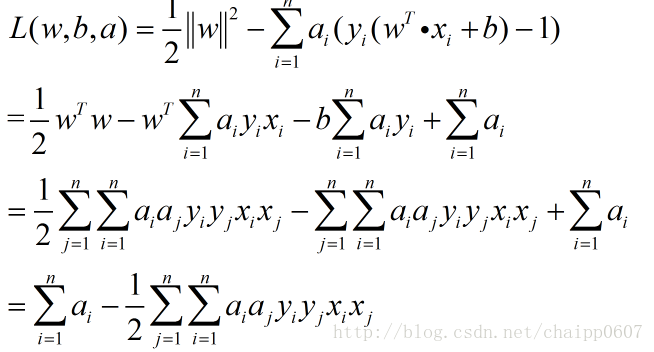
è¿éåå¾çæè¿°

所以问题被转化成为： 
 
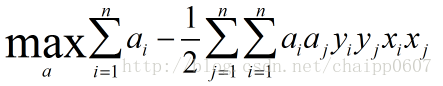
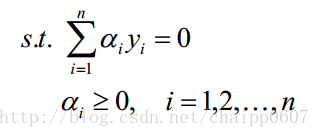
 è¿éåå¾çæè¿°

è¿éåå¾çæè¿°
注意这里的约束条件有n+1个。

添加符号，再一次转化条件：

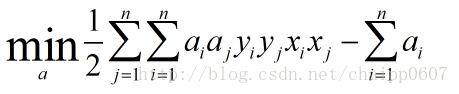
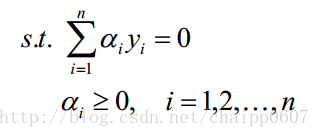
è¿éåå¾çæè¿°

è¿éåå¾çæè¿°

注：对偶问题的转换需要满足KKT条件 ，关于SVM的KKT条件详细介绍见这里和这里。

至此，原始问题通过满足KKT条件，已经转化成了对偶问题。而求解这个对偶学习问题，分为3个步骤：首先要让L(w，b，a) 关于 w 和 b 最小化，然后求对的极大，最后利用SMO算法求解对偶问题中的拉格朗日乘子。关于SMO算法见这里。

到目前为止，我们的 SVM 还比较弱，只能处理线性的情况，下面我们将引入核函数，进而推广到非线性分类问题。

核函数

关于核函数内容可见：支持向量机导论（理解SVM的三种境界）

引入松弛因子

为什么要引入松弛因子？

从前面的内容来看，SVM理论可以完美的找到正负样本间的最大的分类间隔，这意味着不仅仅可以实现对训练数据的分类，还保证了决策平面是最理想的。那么SVM为什么还要引入松弛因子呢？

最开始讨论支持向量机的时候，我们就假定，数据是线性可分的，亦即我们可以找到一个可行的超平面将数据完全分开。后来为了处理非线性数据，使用 核方法对原来的线性 SVM 进行了推广，使得非线性的的情况也能处理。虽然通过映射将原始数据映射到高维空间之后，能够线性分隔的概率大大增加，但是对于某些情况还是很难处理。

    例如可能并不是因为数据本身是非线性结构的，而只是因为数据有噪音。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。例如下图：

                                             

   用黑圈圈起来的那个蓝点是一个 outlier ，它偏离了自己原本所应该在的那个半空间，如果直接忽略掉它的话，原来的分隔超平面还是挺好的，但是由于这个 outlier 的出现，导致分隔超平面不得不被挤歪了，变成图中黑色虚线所示（这只是一个示意图，并没有严格计算精确坐标），同时 margin 也相应变小了。当然，更严重的情况是，如果这个 outlier 再往右上移动一些距离的话，我们将无法构造出能将数据分开的超平面来。

  为了处理这种情况，SVM 允许数据点在一定程度上偏离一下超平面。例如上图中，黑色实线所对应的距离，就是该 outlier 偏离的距离，如果把它移动回来，就刚好落在原来的 超平面 蓝色间隔边界上，而不会使得超平面发生变形了。

所以引入松弛因子有两点考虑：

                                         1、存在偏离总体样本的样本点使得求得的超平面并非最优超平面；

                                         2、存在严重偏离总体样本的样本点使得样本结构线性不可分。

新的目标函数  

在原有的约束条件上加入一个松弛因子，要求\zeta>0，那么约束条件变为： 

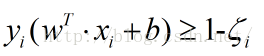
                                             è¿éåå¾çæè¿°

很显然，由于松弛因子是一个正数，那么新的约束条件一定没有原来的条件“严格”，也就是松弛了。 
同时，目标函数同样发生变化：

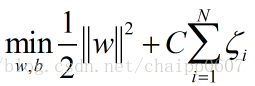
                                                 è¿éåå¾çæè¿° 

这个目标函数的变化是通过间隔松弛向量的范数定义的泛化误差界推导的出来，但是这不是SVM的重点，重点在于改变的目标函数对决策平面的影响。 
除了一阶软间隔分类器，SVM的目标函数还有二阶软间隔分类器的形式：

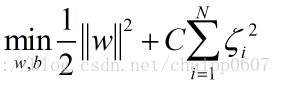
                                                   è¿éåå¾çæè¿°

而无论是上述哪种情况，实际上都是为目标函数引入一个损失。其中  是一个参数，用于控制目标函数中两项（“寻找 margin 最大的超平面”和“保证数据点偏差量最小”）之间的权重,也叫惩罚因子。

惩罚因子的大小决定了对离群点的容忍程度（松弛的程度），比如，如果C是一个非常大的值，那么很小的松弛因子都会让目标函数的值边的很大，然后目标是在求一个最小值，这就意味着哪怕是个很小的松弛都不愿意容忍。还有一种极端的情况是如果C选定成一个无穷大的值，那么软分类间隔问题（soft margin）会退化称为一个硬分类间隔问题（hard margin）。

可以拿一个很直观的例子说明惩罚因子C的影响，C越大意味着对训练数据而言能得到很好的分类结果，但是同时最大分类间隔就会变小，毕竟我们做模型不是为了在训练数据上有个多么优异的结果。相反的，如果C比较小，那么间隔就会变大，模型也就有了相对而言更好的泛化能力。

最后新的目标函数（采用一阶范式）： 

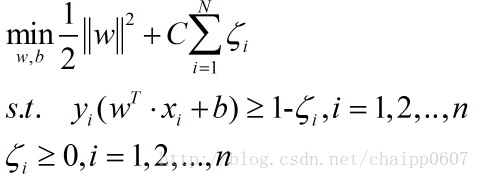
                            è¿éåå¾çæè¿°

这里的约束条件是2n个。

软分类间隔问题的求解

上式目标函数的求解步骤推导与前面一样，具体可见这里。

最终的对偶问题就是：

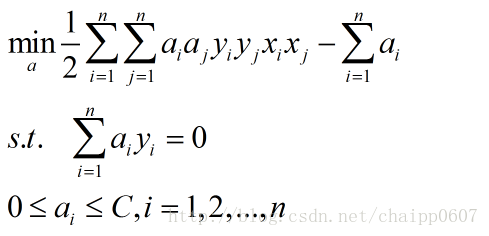
                                   è¿éåå¾çæè¿°

这个结果和原对偶问题的结果很像，只是约束条件多了上线C。最后利用SMO算法求解即可找到超平面参数。

                                               

总结

SVM的思想是找到划分类别的最优超平面，使得分类间隔最大化。根据超平面方程得到最初分类函数，最大化分类间隔，max1/||w||，min1/2||w||^2，凸二次规划问题，利用拉格朗日函数转化为求原问题的对偶问题（满足KKT条件），利用SMO算法求解对偶问题，都为寻找一个最优解，一个最优分类平面。一步步梳理下来，为什么这样那样，太多东西可以追究，最后实现。

应用


SVM在很多诸如文本分类，图像分类，生物序列分析和生物数据挖掘，手写字符识别等领域有很多的应用，但或许你并没强烈的意识到，SVM可以成功应用的领域远远超出现在已经在开发应用了的领域。

 

SVM面试笔试问题：https://blog.csdn.net/szlcw1/article/details/52259668

参考

https://mp.csdn.net/postedit   最通俗易懂的导出SVM模型

https://blog.csdn.net/v_JULY_v/article/details/7624837   最详细的介绍，理论很强

https://blog.csdn.net/chaipp0607/article/details/75949812  详细而又通俗易懂