
我的毕设题目定为《基于机械臂触觉伺服的物体操控研究》,这个系列主要用于记录做毕设的过程。
轨迹规划是机器人绕不过去的话题,其目的是为了让机器人的运动更加的平滑。对于四足机器人,贝赛尔曲线的应用比较普遍。而对于机械臂,则需要根据场景来选择适合的规划方式,常用的有样条曲线和LSPB等。下面我将给出四种比较常用的轨迹规划方法的推导过错,以及相应的代码,以供读者参考。
注:所有给出的代码主要是为了展示对应算法的编程思路,虽然代码都验证过可行,但是由于还需要关联其它库,所以无法直接运行。也建议读者根据自己的要求进行重新编写。等我的毕设答辩结束后,我会将整份工程进行开源。
规划时间
因为轨迹规划所得的轨迹是关于时间t的函数,在实际应用时,为了保证机械臂运动的平滑,一般要将运动速度设为恒值,即根据过程点的距离来确定规划时间。这里给出一种思路以供参考。
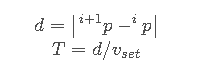
vset:人为设定的速度值
代码实现
/**
* @brief
* @param p1 point 1
* @param p2 point 1
* @param vel motion velocity
*/
template <typename T>
T getDeltaTime(Vec18<T> p1, Vec18<T> p2, T vel) {
T distance = 0;
for (int i = 0; i < 3; i++) {
distance += abs(p1(i) - p2(i));
}
/* set delta time refer to distance */
return distance / vel;
}
1. 线性插值
这种方式假定机械臂以直线的形式在给定过程点之间运动,并且因为拐角的加速度值不可求,所以我们可以假定其一直做匀速运动,加速度恒为零。
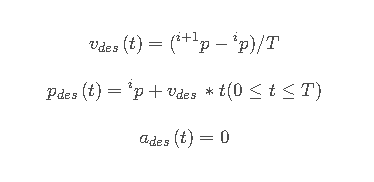
代码实现
/**
* @brief compute Line trajectory
* @param points control points(including start point and end point)
* @param resolution the point number between two control points
*/
template <typename T>
void LineTrajectory(std::vector<Vec18<T>> points, int resolution) {
int points_num = points.size();
Vec18<T> point;
Vec6<T> pDes, vDes, aDes;
/* Set acceleration to zero */
aDes.setZero();
/* push back start point */
_trajectory.push_back(points[0]);
for (int i = 0; i < points_num - 1; i++) {
T dt = getDeltaTime(points[i], points[i + 1]) / (resolution + 1);
for (int j = 1; j <= resolution + 1; j++) {
/* only consider position */
for (int k = 0; k < 6; k++) {
vDes(k) = (points[i + 1](k) - points[i](k)) / (resolution + 1);
pDes(k) = points[i](k) + vDes(k) * j;
}
point.block(0, 0, 6, 1) = pDes;
point.block(6, 0, 6, 1) = vDes * getDeltaTime(points[i], points[i + 1]);
point.block(12, 0, 6, 1) = aDes;
_trajectory.push_back(point);
_deltaT.push_back(dt);
}
}
}
2. 贝赛尔曲线
贝赛尔曲线的推导可以参考我之前的文章。
贝赛尔曲线学习
位置
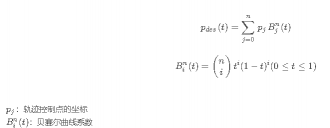
注:n = 控制点总数(包含起点和终点) - 1
速度,加速度

代码实现
/**
* @brief compute Bezier trajectory
* @param points control points(including start point and end point)
* @param resolution trajectory points number
*/
template <typename T>
void BezierTrajectory(std::vector<Vec18<T>> points, int resolution) {
int poinets_num = points.size(); /* the number of control points */
T dt = 1 / (T)resolution;
Vec18<T> point;
T pDes, vDes, aDes;
/* push back start point */
_trajectory.push_back(points[0]);
/* get motion time */
T motion_T = 0;
for (int k = 0; k < poinets_num - 1; k++) {
motion_T += getDeltaTime(points[k], points[k + 1]);
}
motion_T /= resolution;
/* apply Bezier algorithm */
point.setZero();
for (int i = 1; i <= resolution; i++) {
/* only consider position */
for (int j = 0; j < 6; j++) {
pDes = 0;
vDes = 0;
aDes = 0;
for (int k = 0; k < poinets_num; k++) {
pDes += CombinatorialNumber(poinets_num - 1, k) * points[k](j) * pow(dt * i, k) *
pow((1 - dt * i), poinets_num - 1 - k);
vDes += CombinatorialNumber(poinets_num - 1, k) * points[k](j) *
FirstDerivation(dt * i, poinets_num - 1, k);
aDes += CombinatorialNumber(poinets_num - 1, k) * points[k](j) *
SecondDerivation(dt * i, poinets_num - 1, k);
}
point(j) = pDes;
point(j + 6) = vDes;
point(j + 12) = aDes;
}
/* Add to trajectory */
_trajectory.push_back(point);
_deltaT.push_back(motion_T);
}
}
/**
* @brief return the first derivation value of t^i((1-t)^(n-i))
*
*/
template <typename T>
T FirstDerivation(T t, T n, T i) {
T value = 0;
if ((i - 1) >= 0)
value += i * pow(t, i - 1) * pow(1 - t, n - i);
if ((n - i - 1) >= 0)
value += -(n - i) * pow(t, i) * pow(1 - t, n - i - 1);
return value;
}
/**
* @brief return the second derivation value of t^i((1-t)^(n-i))
*
*/
template <typename T>
T SecondDerivation(T t, T n, T i) {
T value = 0;
if ((i - 2) >= 0 && (n - i) >= 0)
value += i * (i - 1) * pow(t, i - 2) * pow(1 - t, n - i);
if ((i - 1) >= 0 && (n - i - 1) >= 0)
value += -2 * i * (n - i) * pow(t, i - 1) * pow(1 - t, n - i - 1);
if (i >= 0 && (n - i - 2) >= 0)
value += (n - i) * (n - i - 1) * pow(t, i) * pow(1 - t, n - i - 2);
return value;
}
/* compute Statistics combination number */
int CombinatorialNumber(int n, int i)
{
int out;
out = factorial(n);
out /= factorial(i) * factorial(n-i);
}
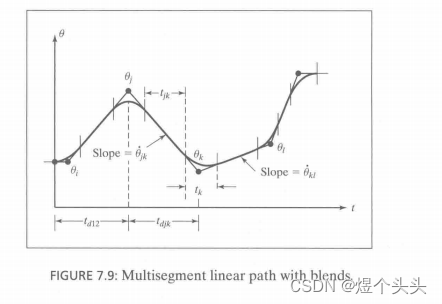
3. LSPB曲线(抛物线-直线-抛物线)
LSPB是机械臂最常用的轨迹规划算法之一,但要注意的是,LSPB得到的轨迹不经过中间点,
并且过渡区间的加速度需要在符合要求的区间内自行定义。一般来说,加速度的取值要足够大,以保证各路径段有足够长的直线区段。
只有起始点和终点的情况
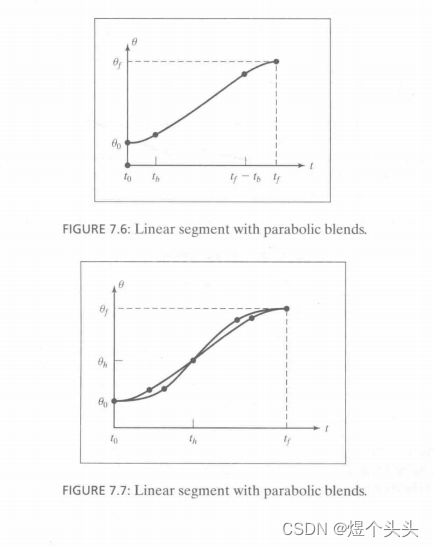
参数定义
t h : 时间中点
θ h : 位置中点
θ b : 过渡区段终点位置
θ ¨ : 过渡区段加速度
过渡区终点速度等于直线部分速度
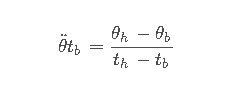
运动学公式
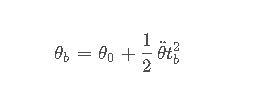
联立得

加速度要满足的条件

根据运动学公式,即可得到各个分段中的轨迹位置,速度及加速度(这里给出位置的公式,速度和加速度简单求导即可)
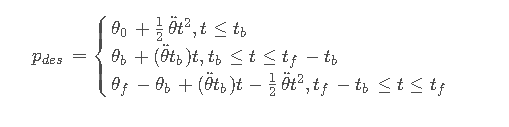
带有中间点的情况
对于内部路径点
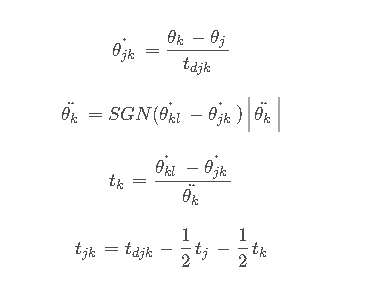
对于第一个路径段,令线性区段速度的两个表达式相等
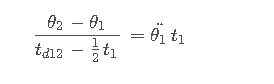
由此即可解出其余量

对于最后一个路径段,与一个路径点处理类似
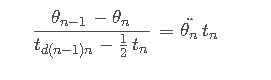
由此即可解出其余量
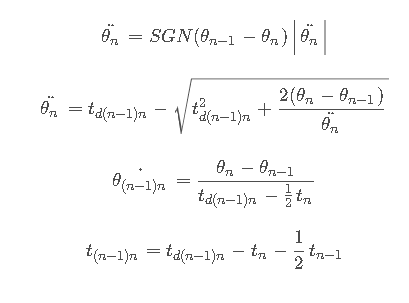
加速度要满足的条件

代码实现
/**
* @brief compute LSPB trajectory
* @param points control points(including start point and end point)
* @param resolution the point number between two control points
*/
template <typename T>
void pathPlanner<T>::LSPBTrajectory(std::vector<Vec18<T>> points, int resolution) {
int len = points.size();
std::vector<Vec18<T>> trajectory(resolution * (len - 1) + len);
;
/* push back start point */
trajectory[0] = points[0];
std::vector<T> acc(len);
std::vector<T> deltaT(len - 1);
/* define acceleration and deltaT to constant value */
for (int i = 0; i < len; i++) {
acc[i] = 150.;
if (i != len - 1)
deltaT[i] = getDeltaTime(points[i], points[i + 1]);
}
std::vector<T> Vd(len - 1); /* line velocity between two points */
std::vector<T> Td(len - 1); /* line motion time between two points */
std::vector<T> Ti(len); /* nearby time of a point */
T dp, a_;
T pDes, vDes, aDes;
for (int j = 0; j < 6; j++) {
if (len == 1)
return;
/* no middle points */
else if (len == 2) {
dp = points[1](j) - points[0](j);
a_ = sign(dp) * abs(acc[0]);
assert(abs(a_) >= 4 * abs(dp / pow(deltaT[0], 2)));
Ti[0] = 0.5 * deltaT[0] - sqrt((pow(a_ * deltaT[0], 2) - 4 * a_ * dp)) / (2 * a_);
Ti[1] = Ti[0];
Vd[0] = a_ * Ti[0];
Td[0] = deltaT[0] - 2 * Ti[0];
}
/* have middle points */
else {
/* compute start time and velocity */
dp = points[1](j) - points[0](j);
a_ = sign(dp) * abs(acc[0]);
assert((pow(deltaT[0], 2) - 2. * dp / a_) >= 0);
Ti[0] = deltaT[0] - sqrt(pow(deltaT[0], 2) - 2. * dp / a_);
Vd[0] = dp / (deltaT[0] - 0.5 * Ti[0]);
/* compute velocity of middle points */
for (int i = 1; i < len - 2; i++) {
dp = points[i + 1](j) - points[i](j);
Vd[i] = dp / deltaT[i];
}
//* compute end time and velocity */
dp = points[len - 1](j) - points[len - 2](j);
a_ = sign(-dp) * abs(acc[len - 1]);
assert((pow(deltaT[len - 2], 2) + 2. * dp / a_) >= 0);
Ti[len - 1] = deltaT[len - 2] - sqrt(pow(deltaT[len - 2], 2) + 2. * dp / a_);
Vd[len - 2] = dp / (deltaT[len - 2] - 0.5 * Ti[len - 1]);
/* compute time of middle points */
for (int i = 1; i < len - 1; i++) {
a_ = sign(Vd[i] - Vd[i - 1]) * abs(acc[i]);
Ti[i] = (Vd[i] - Vd[i - 1]) / a_;
}
/* compute delta time of middle points */
for (int i = 1; i < len - 2; i++) {
Td[i] = deltaT[i] - 0.5 * Ti[i] - 0.5 * Ti[i + 1];
}
/* supplemental data */
Td[len - 2] = deltaT[len - 2] - Ti[len - 1] - 0.5 * Ti[len - 2];
Td[0] = deltaT[0] - Ti[0] - 0.5 * Ti[1];
}
T dt, t_;
for (int i = 0; i < len - 1; i++) {
/* delta time between two points */
dt = deltaT[i] / (T)(resolution + 1);
/* start and end point */
double start = points[i](j);
double end = points[i + 1](j);
for (int k = 1; k <= resolution + 1; k++) {
/* define value refer to time range */
t_ = k * dt;
/* judge start or end point */
T Tb1 = (i == 0) ? Ti[i] : Ti[i] / 2.;
T Tm = Tb1 + Td[i];
T Tb2 = Tm + (i == len - 2) ? Ti[i + 1] : Ti[i + 1] / 2.;
if (t_ <= Tb1) {
pDes = start + 0.5 * acc[i] * pow(t_, 2);
vDes = acc[i] * t_;
aDes = acc[i];
} else if (t_ > Tb1 && t_ < Tm) {
pDes = start + 0.5 * acc[i] * pow(Ti[i], 2) + Vd[i] * (t_ - Tb1);
vDes = Vd[i];
aDes = 0;
} else {
pDes = start + 0.5 * acc[i] * pow(Ti[i], 2) + Vd[i] * Td[i] + Vd[i] * (t_ - Tm) -
0.5 * acc[i] * pow((t_ - Tm), 2);
vDes = -acc[i] * (t_ - Tm);
aDes = -acc[i];
}
trajectory[i * (resolution + 1) + k](j) = pDes;
trajectory[i * (resolution + 1) + k](j + 6) = vDes;
trajectory[i * (resolution + 1) + k](j + 12) = aDes;
/* set delta time */
if (!j) {
_deltaT.push_back(dt);
}
}
}
}
/* Add to trajectory */
for (int i = 0; i < resolution * (len - 1) + len; i++) {
_trajectory.push_back(trajectory[i]);
}
}
4. 三次样条法
根据过程点列写方程,并写成矩阵形式。
三次样条表示形式
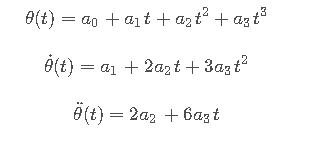
根据过程点列写方程
在一个时间段内,每个三次曲线的起始时刻t=0。终止时刻t=t fi(1≤i≤n),过程点为θ i
要求解的参数

初末速度为0
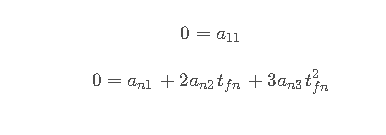
位置满足设定值

中间点速度和加速度一致

联立即可求解。
代码实现
/**
* @brief compute Spline trajectory
* @param points control points(including start point and end point)
* @param resolution the point number between two control points
*/
template <typename T>
void SplineTrajectory(std::vector<Vec18<T>> points, int resolution) {
T pDes, vDes, aDes, a_;
int len = points.size();
/* Set start point */
std::vector<Vec18<T>> trajectory(resolution * (len - 1) + len);
trajectory[0] = points[0];
/* set delta time */
std::vector<T> dT(len - 1);
for (int i = 0; i < len - 1; i++) {
// dT[i] = 1;
dT[i] = getDeltaTime(points[i], points[i + 1]);
}
const int M_SIZE = 4 * (len - 1);
/* deine variable matrix */
Eigen::MatrixXd A;
A.setZero(M_SIZE, M_SIZE);
Eigen::VectorXd X(M_SIZE);
Eigen::VectorXd b(M_SIZE);
Eigen::VectorXd solve(M_SIZE);
for (int j = 0; j < 6; j++) {
int index = 0;
/* Set end velocity to zero */
A(index, 1) = 1;
b(index) = 0;
index++;
A(index, 4 * (len - 2) + 1) = 1;
A(index, 4 * (len - 2) + 2) = 2 * dT[len - 2];
A(index, 4 * (len - 2) + 3) = 3 * pow(dT[len - 2], 2);
b(index) = 0;
index++;
for (int i = 0; i < len - 1; i++) {
/* position */
A(index, i * 4 + 0) = 1;
b(index) = points[i](j);
index++;
A(index, i * 4 + 0) = 1;
A(index, i * 4 + 1) = dT[i];
A(index, i * 4 + 2) = pow(dT[i], 2);
A(index, i * 4 + 3) = pow(dT[i], 3);
b(index) = points[i + 1](j);
index++;
/* velocity */
if (i != 0) {
A(index, (i - 1) * 4 + 1) = 1;
A(index, (i - 1) * 4 + 2) = 2 * dT[i - 1];
A(index, (i - 1) * 4 + 3) = 3 * pow(dT[i - 1], 2);
A(index, i * 4 + 1) = -1;
b(index) = 0;
index++;
}
/* acceleration */
if (i != 0) {
A(index, (i - 1) * 4 + 2) = 2;
A(index, (i - 1) * 4 + 3) = 6 * dT[i - 1];
A(index, i * 4 + 2) = -2;
b(index) = 0;
index++;
}
}
/* solve function */
X = A.colPivHouseholderQr().solve(b);
double dt, t_;
for (int i = 0; i < len - 1; i++) {
/* delta time between two points */
dt = dT[i] / (resolution + 1);
for (int k = 1; k <= resolution + 1; k++) {
/* substitute into cubic polynomial */
t_ = k * dt;
pDes = X(i * 4) + X(i * 4 + 1) * t_ + X(i * 4 + 2) * pow(t_, 2) + X(i * 4 + 3) * pow(t_, 3);
vDes = X(i * 4) + X(i * 4 + 1) + 2 * X(i * 4 + 2) * t_ + 3 * X(i * 4 + 3) * pow(t_, 2);
aDes = 2 * X(i * 4 + 2) + 6 * X(i * 4 + 3) * t_;
trajectory[i * (resolution + 1) + k](j) = pDes;
trajectory[i * (resolution + 1) + k](j + 6) = vDes;
trajectory[i * (resolution + 1) + k](j + 12) = aDes;
/* set delta time */
if (!j) {
_deltaT.push_back(dt);
}
}
}
}
/* Add to trajectory */
for (int i = 0; i < resolution * (len - 1) + len; i++) {
_trajectory.push_back(trajectory[i]);
}
}





评论(1)
您还未登录,请登录后发表或查看评论