首先感谢古月居转载我的文章，但是本文有很多乱码和不清晰的地方影响阅读体验，如果对本文感兴趣，欢迎大家去看我的知乎原帖，同时欢迎留言讨论！

接上一帖，我们已经介绍完了旋转矩阵和角速度的相关知识，接下来我们来看旋转的另一种表示方法，指数坐标（Exponential Coordinate ）。

那么指数坐标（Exponential Coordinate ）的作用是什么呢，这里依旧用原书给出的定义：

The exponential coordinates parametrize a rotation matrix in terms of a rotation axis (represented by a unit vector  ) and an angle of rotation θ about that axis; the vector then serves as the three-parameter exponential coordinate representation of the rotation.

用指数坐标  来描述旋转矩阵R可以这样解释：

（1）如果定系s绕  轴旋转θ,新的位置相对于定系将由旋转矩阵R表达

另外两个描述一时想不出如何好的翻译，就先贴在这里，有知道的大佬欢迎来评论区讨论啊

（2）the angular velocity  expressed in {s} such that, if a frame initially coincident with {s} followed  for one unit of time (i.e.,  is integrated over this time interval), its final orientation would be expressed by R.

(3)the angular velocity  expressed in {s} such that, if a frame initially coincident with {s} followed  for θ units of time (i.e., θ is integrated over this time interval) its final orientation would be expressed by R.

之后继续来讨论一下需要的基础知识，线性微分方程的一些内容：

有这样的一个方程，初始条件为  ：

根据高等数学的知识，我们知道这个方程的解为：

这时候，如来神展就要发功了，利用  的麦克劳林级数，有：

进阶，现在换成向量微分方程，初始条件不变：

这个方程的解为：

根据矩阵分析中的知识

可以证明，如果A是常数且有限，那么这个级数总是保证收敛,具体请看矩阵分析相关的书。

继续，对于  的任意方阵A和B，下式总是成立：

如果: 

那么：

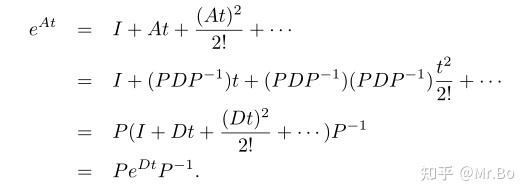
如果D是一个对角阵，那么结果将非常好计算。

推导了这么半天，总结一下：

向量微分方程 ，在初始条件为  时，解为  ，式中：

矩阵指数  有如下性质：

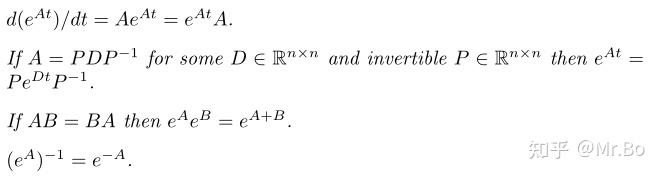
这样，热身工作结束，接下来进入旋转指数坐标

旋转指数坐标可以看成：

（1）绕某轴  （  ）旋转 

（2）将（1）中两者相乘形成的三维向量 

如下图所示，向量p(0)绕轴经过时间t旋转θ为 

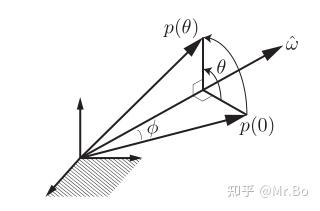
根据我们之前的结论，这样p（t）矢量末端的线速度  可以表示为：

这个式子和我们之前介绍的向量微分方程如出一辙，因此它的解为：

那意味着p（0）绕轴旋转后的新位置为：

接着我们进一步展开这个式子，由于  是斜对称阵，运算一下就有 

这样：

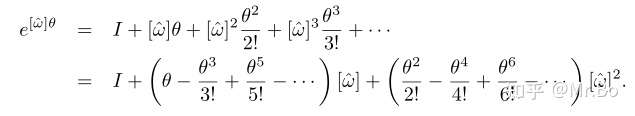
继续化简，可以看出括号内正好和sin和cos的麦克劳林级数有联系：

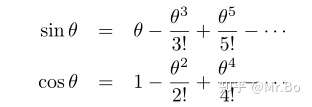
这样就有了下面这个描述：

对于一个向量  ，  是任意标量，  是单位向量,  , 绕轴 旋转  的旋转矩阵就可以写成：

上式就是著名的Rodrigues’formula。

通过这种方式，我们就可以很方便的完成旋转操作。比如我们要对3x3的矩阵B进行旋转，那么  表示在定系中绕  轴旋转θ，  表示在动系中绕  轴旋转θ。

纯理论是不是过于抽象，这里我们举个例子：

图中定系s绕  旋转30°，那么旋转矩阵就可以表示为：

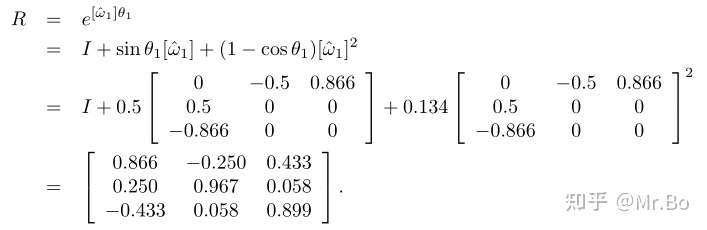
假设定系s的矩阵是单位阵I，那么转动后的新位置就是R，注意角度不同，旋转后的位置不一致。

接下来进一步进行讨论：

如果  表示旋转矩阵R的指数坐标，那么斜对称阵  就是旋转矩阵R的矩阵对数（matrix logarithm）。通过这种方式，就在旋转矩阵和向量之间搭建了桥梁：

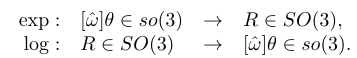
旋转矩阵表示为：

为了推导矩阵对数，我们先将Rodrigues’formula展开：

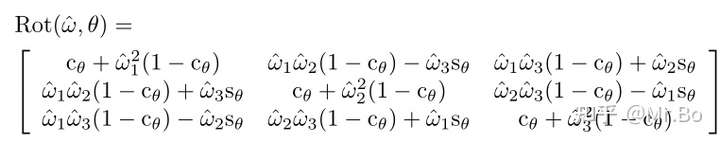
式中，  ， ,由于旋转矩阵是对称阵，对矩阵减去它的转置后我们可以得到：

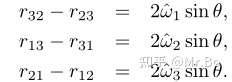
上式中  ，就有：

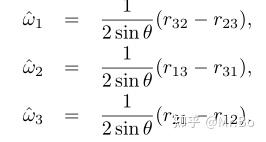
上面解出的式子可以表示为斜对称阵：

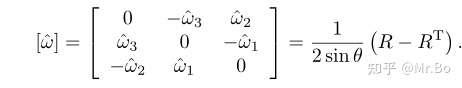
由于  的存在，这里得做出讨论：

当  时，引入矩阵的迹：

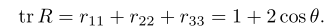
因为  是单位向量，因此  ，那么对于任意 满足  且  ，旋转矩阵R就可以用指数坐标  来描述，其中：

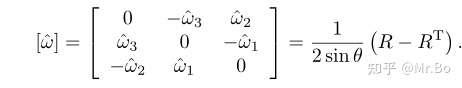
当 时，  ,

当k为偶数时，这意味着已经绕轴转回了  ，所以转轴  没有被定义。

当k为奇数时，旋转矩阵可以表示为：

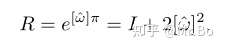
继续运算就有：

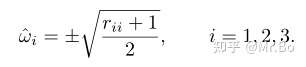
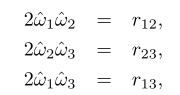
由于旋转矩阵是对称阵，因此所有元素都计算完毕了。

到这里，矩阵对数的推导就结束了，总结一下：

对于给出的旋转矩阵  ,绕单位旋转轴  旋转一个角度  ,向量  表示旋转矩阵R的指数坐标，斜对称阵  表示旋转矩阵R的矩阵对数（matrix logarithm ）。

就有以下情况：

（1）如果  ,意味着  且旋转轴  没有被定义

（2）如果  ，意味着  ,旋转轴  的表示为下式三者任意一个：

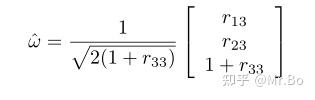
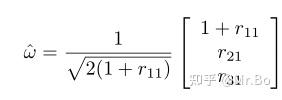
（3）如果  ,那么：

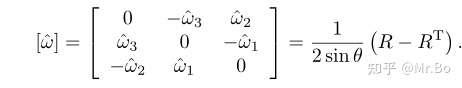
满足上述三个条件中的一个，对于一个旋转矩阵R的指数坐标就存在一个矩阵对数。

接下来介绍刚体运动或齐次变换矩阵：

先来说明一些符号，刚体运动的矩阵用T来表示，转轴表示为S，指数坐标就为  ，这样速度向量  ，动系b相对于定系s的转动用旋转矩阵  来描述，动系b的原点相对于定系的位置用向量 来描述，这样：

一个 special Euclidean group  ,被称为刚体运动或齐次变换矩阵，就写作下式：

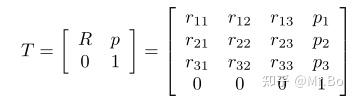
它也可以写成这个形式  ，这个在前面的文章中我们介绍过了，可以返回去看一下。

上面的式子是描述三维空间刚体运动的矩阵，那么刚体在二维平面的运动如何表示呢，其实定义方式一样：

一个 special Euclidean group  ,  ,  ,那么二维平面内刚体运动的矩阵就为：

常用的形式就是：

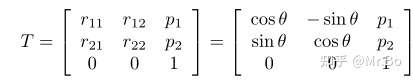
有了上面的矩阵，我们就可以描述刚体的运动，接下来对刚体运动矩阵的性质进行探究：

变换矩阵的逆矩阵为：

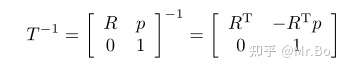
两个变换矩阵的乘积还是一个变换矩阵，但是矩阵乘法不满足交换律，因此：

但是这里出现了一个问题，变换矩阵是4x4的，但是在坐标系里表达的向量x是1x3的，可以通过添1的方法把向量x扩展成4维的，和变换矩阵相乘就可以对向量x进行几何操作，如下式：

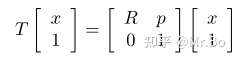
如果我们用向量坐标来描述刚体上的点，那么通过上式就能很好的描述刚体的运动。

对于变换矩阵T，它有着和旋转矩阵一致的性质，这里就不再赘述，矩阵内部值不同，代表的含义也不同，比如只旋转不平移的矩阵：

只平移不旋转的矩阵：

变换矩阵可以完成很多操作，个人感觉本书这里讲的不是很好，大家可以去看看图形变换的矩阵方法，相信会对变换矩阵有一个深入的了解。

写到这里，我么所需要的所有预备知识就介绍完毕了，接下来我们将讨论刚体运动的线速度，角速度组成的twist，力和力矩组成的wrench，这就需要开新帖了