在线性最小二乘法中我们知道了通过测量数据构建齐次方程组来拟合最优系数的基本步骤,其中包括直接法即所有系数均为线性形式;广义法即通过构建误差的最小化形式求解系数,其相比直接法运算量固定,更加适合计算机编程;间接法其主要是通过换元处理将一些模型中简单的非线性元素替换,从而将其转换为可采用前两种方法的线性系统。以之前提到的二位圆拟合例子为例,其一般式方程如下:
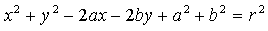
上式中存在着非线性系数部分,无法采用直接法将其作为待求矩阵向量,通过采用间接法定义如下变量我们构建出了一个新的线性系统模型,进而可以采用直接法或广义法来求解中间系数:
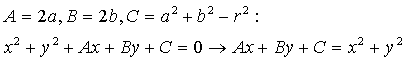
最终,基于中间系数拟合结果结合其定义和圆半径物理性质可以确定原未知系数的结果如下:
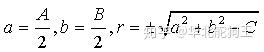
综上,对于处理一些典型的非线性部分如某个系数独立的二阶非线性项,采用间接法能保证我们继续使用线性最小二乘法,但在实际情况中除了以上给出几个比较特殊的例子,许多非线性模型中存在更复杂的非线性形式,如何定义合适的中间系数变得开始玄学,这有点像高中数学中许多代数变换或消元处理仅在某种形式下才能简化问题,而大部分这些中间变量的定义方式都是题目直接给出、可参考到,但当我们遇到完全没有见过的系统模型还想借鉴以前的定义方法就不太实际了,这也是我们在很多应用中明明知道最小二乘法能解决它却无从下手的原因。
对于上述模型更准确的定义是求解一个非线性最小二乘问题,同样网上也能查到许多相关介绍,常用的方法包含梯度下降、牛顿法、高斯牛顿法和LM法,同样下面还是以一种个人理解的思路介绍下在数值优化、SLAM等领域中最常用的两种非线性最小二乘问题求解的方法。
(1)高斯牛顿法
高斯牛顿法有许多可参考的资料给出了详细推导的过程,以
中给出的推导过程较为清晰,对一个非线性最小二乘问题,我们通过系统模型定义了误差方程为:

其中矩阵A中包含着平方关系、对数关系、指数关系、三角函数关系等无法采用换元代替的非线性元素,则采用泰勒级数展开f(x)并只保留1阶项有:

如f(x)中包含多元系数,则偏导数为雅克比矩阵J,考虑最小二乘法的目标是最小化误差的平方和可以得到:
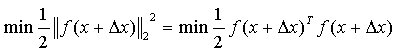
带入泰勒展开的结果有:
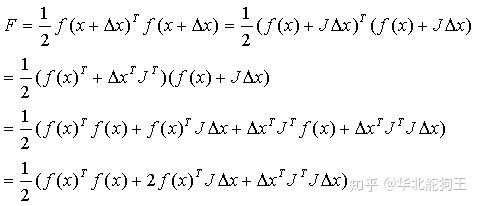
与线性最小二乘法一样,对上式要取到极小值可以对x增量求导后等式为0,则有:

则通过求解上式只要H矩阵可逆就可以求取对系数x的修正增量,这也是牛顿高斯迭代计算的核心,但该矩阵如果不满足会导致计算出的步长太大使得结果发散,这也是高斯牛顿法的缺点之一,则采用高斯牛顿法迭代求解未知参数的流程如下:
A. 给定未知参数x的初始值x0
B. 循环迭代开始,首先构建误差方程f(x),求取其对应各未知参数x的偏导数构成雅克比矩阵J,此时同样有两种处理方法一种类似之前线性最小二乘法中的直接法,即假设有N组数据我们直接求取每一组数据对应的J并不断按行增广该矩阵,即:

C. 其中求取偏导数时使用当前迭代的系数和每组对应的测量值与参数值,之后求取对应的H和B矩阵:
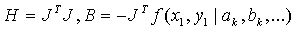
D. 则当H矩阵可逆时就可以求取得到对应的x增量并对当前参数估计结果进行更新:
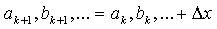
E. 持续上述步骤直到x增量足够小或者超过设定的迭代次数。
与直接法的问题类似当我们有N个观测数据时矩阵J的维数将随着观测数据的增加而变大,这不利于加速运算在广义法中我们知道通过求取参数平均值的方式能保证计算的复杂度,同样对于高斯牛顿法我们也可以采用相同的处理方式来计算H和B:
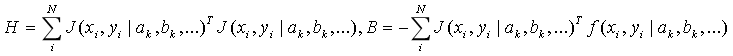
综上,以上就是高斯牛顿法的具体计算步骤,下面我们还是以之前拟合圆为例,这次我们不替换中间变量直接读非线性部分采用高斯牛顿法处理,则首先构建误差方程:

则对第i组测量数据对于的矩阵Ji为:

进一步累加计算H和B矩阵的平均值,然后使用x增量修正当前系数直到其收敛,采用相同数据的matlab仿真如下:
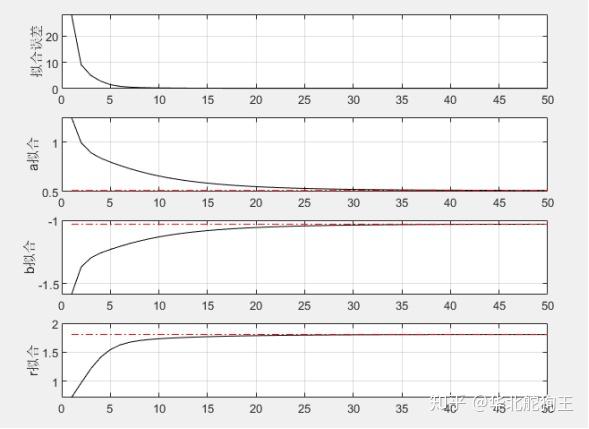
可以看到拟合的误差随迭代次数增加快速下降,相关参数也逐渐趋向实际值,最终拟合的圆结果如下图所示:

相关Matlab仿真代码如下:
close all;
clear all;
clc;
%%拟合圆
%x^2+y^2-2ax-2by+a^2+b^2=r^2
%制造测量
N=70;
Dn=N/2;
d_sampe=5/N;
w=0.15;
a=0.5;
b=-1;
r=1.8;
p_real_circle=[a;b;r]
t = linspace(0,2*pi,100);
xs=sin(t)*r+a;
ys=cos(t)*r+b;
for i=1:N
x(i) = xs(i);
y_real(i)=ys(i);
y_measure(i)=y_real(i)+randn(1)*w;
end
%%间接法
%换元A=-2a B=-2a R=a^2+b^2-r^2
%->x^2+y^2+Ax+By+R=0
Ac(1,:)=[x(1),y_measure(1),1];
bc(1,:)=[-(x(1)^2+y_measure(1)^2)];
for i=2:N
Ac=[Ac(:,:);
x(i),y_measure(i),1];
bc=[bc(:,:);
-(x(i)^2+y_measure(i)^2)];
end
p_temp=pinv(Ac)*bc;
a=-p_temp(1)/2;
b=-p_temp(2)/2;
r=(a^2+b^2-p_temp(3))^0.5;
p_d_circle=[a;b;r]
t = linspace(0,2*pi,100);
x_est=sin(t)*r+a;
y_est=cos(t)*r+b;
%
% figure(3)
% plot(xs,ys,'-.r');
% hold on;
% plot(x,y_measure,'s:b');
% hold on;
% plot(x_est,y_est,'-k');
% grid on;
% axis equal;
% legend('真实曲线','测量值','直接法','广义法')
%%广义法
%换元A=-2a B=-2a R=a^2+b^2-r^2
%->x^2+y^2+Ax+By+R=0
%F=min 0.5/N*(x^2+y^2+Ax+By+R)^2
%Fda= 1/N*sum (x^2+y^2+Ax+By+R)*x =0
%-> 1/N*sum (x^3+xy^2+Ax^2+Bxy+xR) =0
%-> 1/N*sum (Ax^2+Bxy+xR) =-1/N*sum (x^3+xy^2)
sum11=0;
sum12=0;
sum13=0;
sumy1=0;
for i=1:N
x(i) =xs(i);
sum11=sum11+x(i)^2;
sum12=sum12+x(i)*y_measure(i);
sum13=sum13+x(i);
sumy1=sumy1-(x(i)^3+x(i)*y_measure(i)^2);
end
%Fdb= 1/N*sum (x^2+y^2+Ax+By+R)*y =0
%-> 1/N*sum (x^2*y+y^3+Axy+By^2+yR) =0
%-> 1/N*sum (Axy+By^2+yR) =-1/N*sum (x^2*y+y^3)
sum21=0;
sum22=0;
sum23=0;
sumy2=0;
for i=1:N
x(i) =xs(i);
sum21=sum21+x(i)*y_measure(i);
sum22=sum22+y_measure(i)^2;
sum23=sum23+y_measure(i);
sumy2=sumy2-(x(i)^2*y_measure(i)+y_measure(i)^3);
end
%FdR= 1/N*sum (x^2+y^2+Ax+By+R)*1 =0
%-> 1/N*sum (x^2+y^2+Ax+By+R) =0
%-> 1/N*sum (Ax+By+R) =-1/N*sum (x^2+y^2)
sum31=0;
sum32=0;
sum33=0;
sumy3=0;
for i=1:N
x(i) =xs(i);
sum31=sum31+x(i);
sum32=sum32+y_measure(i);
sum33=sum33+1;
sumy3=sumy3-(x(i)^2+y_measure(i)^2);
end
Asg=[sum11/N, sum12/N, sum13/N;
sum21/N, sum22/N, sum23/N;
sum31/N, sum32/N, sum33/N;];
bsg=[sumy1/N;
sumy2/N;
sumy3/N];
p_guan_circle_temp=pinv(Asg)*bsg;
a=-p_guan_circle_temp(1)/2;
b=-p_guan_circle_temp(2)/2;
r=(a^2+b^2-p_guan_circle_temp(3))^0.5;
p_guan_circle=[a;b;r]
t = linspace(0,2*pi,100);
x_estg=sin(t)*r+a;
y_estg=cos(t)*r+b;
%
% figure(4)
% plot(xs,ys,'-.r');
% hold on;
% plot(x,y_measure,'s:b');
% hold on;
% plot(x_est,y_est,'-k');
% hold on;
% plot(x_estg,y_estg,'-m');
% grid on;
% axis equal;
% legend('真实曲线','测量值','直接法','广义法')
%高斯牛顿 不换元
MAX_IT=10;
err_thr=0.02;
% a=0.5;
% b=-1;
% r=0.8;
a_est0=13.8;
b_est0=-11.3;
r_est0=0.1;
a_est=a_est0;
b_est=b_est0;
r_est=r_est0;
%圆一般式方程:x^2+y^2-2ax-2by+a^2+b^2=r^2
a_estd(1)=a_est;
b_estd(1)=-b_est;
r_estd(1)=r_est;
err_all(1)=0;
temp(1)=1;
for j=1:MAX_IT
for i=1:N
f=x(i)^2+y_measure(i)^2-2*a_est*x(i)-2*b_est*y_measure(i)+a_est^2+b_est^2-r_est^2;
J=[-2*x(i)+2*a_est,-2*y_measure(i)+2*b_est,-2*r_est];
if(i==1)
H= J'*J;
B=-J'*f;
f_sum=f*f;
else
H=H+ J'*J;
B=B- J'*f;
f_sum=f_sum+f*f;
end
end
dx=inv(H/N)*B/N;
a_est=a_est+dx(1);
b_est=b_est+dx(2);
r_est=r_est+dx(3);
a_estd(j)=a_est;
b_estd(j)=b_est;
r_estd(j)=r_est;
err_all(j)=f_sum/N;
temp(j)=1;
[a_est,b_est,r_est,f_sum/N];
if(f_sum/N<err_thr)
break;
end
end
p_gn_circle=[a_est;b_est;r_est]
t = linspace(0,2*pi,100);
x_estgn=sin(t)*r_est+a_est;
y_estgn=cos(t)*r_est+b_est;
% figure(5)
% plot(xs,ys,'-.r');
% hold on;
% plot(x,y_measure,'s:b');
% hold on;
% plot(x_estg,y_estg,'-m');
% hold on;
% plot(x_estgn,y_estgn,'-k');
% grid on;
% axis equal;
% legend('真实曲线','测量值','广义法','高斯牛顿')
%
% figure(6)
% subplot(4,1,1)
% plot(err_all,'-k');
% grid on;
% ylabel('拟合误差');
% subplot(4,1,2)
% plot(a_estd,'-k');
% hold on;
% plot(temp*a,'-.r');
% grid on;
% ylabel('a拟合');
% subplot(4,1,3)
% plot(b_estd,'-k');
% hold on;
% plot(temp*b,'-.r');
% grid on;
% ylabel('b拟合');
% subplot(4,1,4)
% plot(abs(r_estd),'-k');
% hold on;
% plot(r*temp,'-.r');
% grid on;
% ylabel('r拟合');(2)LM法
LM法实际是带阻尼的高斯-牛顿方法,其被广泛应用于SLAM中的Bundle Adjustment步骤中,其通过引入新的阻尼项来解决高斯牛顿法中H矩阵不可逆的问题,参考
中的推导过程,对于某非线性最小二乘问题带入展开的泰勒公式后有:
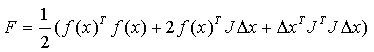
增加阻尼项
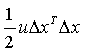
同理对新的公式求x增量的偏导为0,从而寻找极值点:

通过调节u可以让LM算法在牛顿高斯法和梯度下降方法之间无缝地移动,牛顿高斯法将使得算法在解的领域附近快速收敛,梯度下降法使得算法在运行困难时保证代价函数是下降的,从而解决H矩阵病态参数发散的问题,下面我们给定一个初值不合适下的拟合例子对比两算法,仿真结果如下:

可以看到高斯牛顿法由于矩阵病态收敛很慢,而LM法则仍然能快速收敛,牛顿法最终达到总迭代次数时其仍然没有收敛,拟合结果如下图所示:
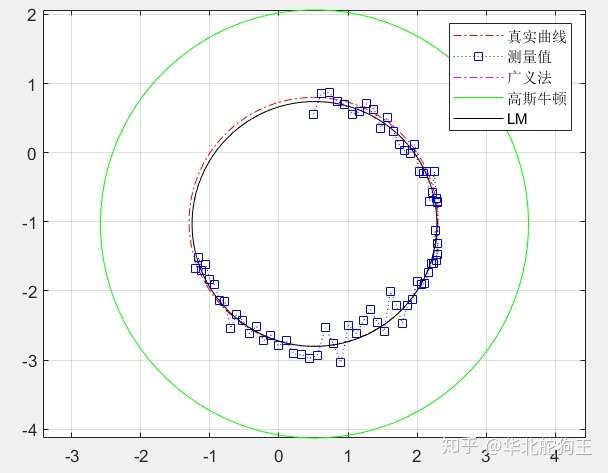
仿真代码如下:
%LM 法不换元
err_thr=0.01;
dlamada=2;
lamda=0.01;
a_est=a_est0;
b_est=b_est0;
r_est=r_est0;
%圆一般式方程:x^2+y^2-2ax-2by+a^2+b^2=r^2
a_estd_lm(1)=a_est;
b_estd_lm(1)=b_est;
r_estd_lm(1)=r_est;
err_all_lm(1)=0;
lamdad(1)=lamda;
temp(1)=1;
for j=1:MAX_IT
for i=1:N
f=x(i)^2+y_measure(i)^2-2*a_est*x(i)-2*b_est*y_measure(i)+a_est^2+b_est^2-r_est^2;
J=[-2*x(i)+2*a_est,-2*y_measure(i)+2*b_est,-2*r_est];
if(i==1)
H= J'*J;
B=-J'*f;
f_sum=f*f;
else
H=H+ J'*J+lamda*eye(3,3);
B=B- J'*f;
f_sum=f_sum+f*f;
end
end
dx=inv(H/N)*B/N;
a_est=a_est+dx(1);
b_est=b_est+dx(2);
r_est=r_est+dx(3);
a_estd_lm(j)=a_est;
b_estd_lm(j)=b_est;
r_estd_lm(j)=r_est;
err_all_lm(j)=f_sum/N;
%计算新的误差
for i=1:N
f_new=x(i)^2+y_measure(i)^2-2*a_est*x(i)-2*b_est*y_measure(i)+a_est^2+b_est^2-r_est^2;
if(i==1)
f_sum_new=f_new*f_new;
else
f_sum_new=f_sum_new+f_new*f_new;
end
end
f_sum_new=f_sum_new/N;
f_sum_last=err_all_lm(j);
%修正lamada比较误差梯度 简单处理
if f_sum_new<f_sum_last
lamda=lamda/dlamada;
else
lamda=lamda*dlamada;
end
if lamda>10000 && 1
lamda=10000;
end
lamdad(j)=lamda;
temp(j)=1;
if(f_sum/N<err_thr)
break;
end
end
p_lm_circle=[a_est;b_est;r_est]
t = linspace(0,2*pi,100);
x_estgn_lm=sin(t)*r_est+a_est;
y_estgn_lm=cos(t)*r_est+b_est;
figure(5)
plot(xs,ys,'-.r');
hold on;
plot(x,y_measure,'s:b');
hold on;
plot(x_estg,y_estg,'-.m');
hold on;
plot(x_estgn,y_estgn,'-g');
hold on;
plot(x_estgn_lm,y_estgn_lm,'-k');
grid on;
axis equal;
legend('真实曲线','测量值','广义法','高斯牛顿','LM')
figure(6)
subplot(5,1,1)
plot(log(err_all),'-.b');
hold on;
plot(log(err_all_lm),'-k');
grid on;
legend('高斯牛顿','LM')
ylabel('log拟合误差');
subplot(5,1,2)
plot((lamdad),'-k');
grid on;
ylabel('lamdad阻尼因子');
subplot(5,1,3)
plot(a_estd,'-.b');
hold on;
plot(a_estd_lm,'-k');
hold on;
plot(temp*a,':r');
grid on;
ylabel('a拟合');
subplot(5,1,4)
plot(b_estd,'-.b');
hold on;
plot(b_estd_lm,'-k');
hold on;
plot(temp*b,':r');
grid on;
ylabel('b拟合');
subplot(5,1,5)
plot(abs(r_estd),'-.b');
hold on;
plot(abs(r_estd_lm),'-k');
hold on;
plot(r*temp,':r');
grid on;
ylabel('r拟合');综上,有了上述非线性优化的工具我们就能较好地解决模型中有非线性部分的最小二乘问题,同时也不需要精心设计换元系数,只需要按标准的算法流程处理就行。
基于该方法我们能将其推广至之前提到的IMU标定、磁场椭球拟合甚至是机器人地形角度估计、足力分配等问题中,而且在理解了算法原理后我们可以自己编程而不使用一些复杂的优化库特别是在些比较老的开发平台中,通过Matlab代码生成快速完成算法在嵌入式平台的部署。







评论(0)
您还未登录,请登录后发表或查看评论