德国人怎么学电机——浅谈电机模型(八)：三相交流电机的旋转磁场理论(一)旋转磁动势

前言

交流电机在德语里叫做“Drehfeldmaschinen”即旋转磁场电机。顾名思义，其原理是基于会圆周旋转的磁场，这个磁场来源于定子绕组的交变电流。对于各种基本类型的交流电机，比如同步电机、异步电机，无论是场、转矩和感应电压的产生，都可以用旋转磁场统一描述其基本原理。借助旋转磁场理论，同步、异步电机在空间上环绕运动的磁场都能被分解出基波和高次谐波，所以交流电机的基本理论得以统一描述。因而可以首先讨论交流电机这个相同点，之后再单独分别讨论同步和异步电机的基本结构和相关理论。

1旋转磁动势

1.1交变的磁动势的分布

因为旋转磁场基于定子绕组的交变电流，所以我们可以先不考虑转子的具体情况。可以只先考察定子。

为了更好理解，我们先考察一个极对极数 $p=1$ ，一对槽对(Nutpaar)，一个匝数为 $N$ 的线圈束，槽缝无穷窄的定子。一捆线圈束(Strang)指的是在每对极占用一对槽的线圈。

而此时转子还没被绕线，而且气隙宽度是恒定的。现在，先通入电流为 $I$ 的直流电。

我们先考察气隙磁场，按照之前的假设，在铁芯部分的磁场场强 $\left(\mu_{Fe } \rightarrow \infty\right)$ 可以被忽略不计,并且气隙磁场是被假设为中心辐散的。对此时所画的半圆磁路应用环路定理得

(8.1) $\oint_{C}^{}\vec H d \vec s=H\left( \alpha \right)\delta-H\left( \alpha+\pi \right)\delta=\Theta\left( \alpha \right)$

当这个与定子同轴心的半圆磁路扫过一定角度时，总的磁动势由被磁回路包围的，上下两段来自同一线圈束的导线上通过的电流强度提供，计算电流密度 $\vec S$ 的积分，得知应为方形分布

(8.2) $\Theta\left( \alpha \right)=\iint_{\vec A\left( \alpha \right)}^{}\vec S d \vec A=\begin{cases} +N\cdot I \text{ ,}& \alpha\in\left( 0,\pi \right) \\ -N\cdot I \text{ ,}&\alpha\in\left( \pi,2\pi \right) \end{cases}$

由于无源的磁通，可得

(8.3) $B\left(\alpha\right)\tau_p l_{Fe}+B\left(\alpha+\pi\right)\tau_p l_{Fe}=0\text{ }\Rightarrow B\left(\alpha+\pi\right)=-B\left(\alpha\right)$

由磁路微观欧姆定理得 $B\left(\alpha\right)=\mu_0 H\left(\alpha\right)$ 代入前式(8.1)

(8.4) $B\left(\alpha\right)=\mu_0 \cdot \frac{\Theta\left( \alpha \right)}{2\delta}=\begin{cases} +\mu_0\frac{N\cdot I }{2\delta}\text{ ,}& \alpha\in\left( 0,\pi \right) \\ -\mu_0\frac{N\cdot I }{2\delta}\text{ ,}&\alpha\in\left( \pi,2\pi \right) \end{cases}$

所以可以推广，在 $p$ 对极的多极布置中，每对极对就划分了一对槽对，那么总匝数为 $N$ 的线圈束在每对槽里要缠绕 $\frac{N}{p}$ 的匝数。

可见，在多极布置里，磁动势的分布只是在圆周上 $p$ 次重复的方形分布。刚刚使用的机械角度 $\alpha$ ，那么如果转换成电磁角度 $\beta$ 应有

(8.5) $\Theta\left(\beta\right)=\begin{cases} +\frac{N }{p}\cdot I\text{ ,}& \beta=p\alpha\in\left(0,\pi\right) \\ -\frac{N }{p}\cdot I\text{ ,}&\beta=p\alpha\in\left( \pi,2\pi\right) \end{cases}$

(8.6) $B\left(\beta\right)=\mu_0 \cdot \frac{\Theta\left( \beta \right)}{2\delta}=\begin{cases} +\mu_0\frac{N\cdot I }{2p\delta}\text{ ,}& \beta=p\alpha\in\left( 0,\pi \right) \\ -\mu_0\frac{N\cdot I }{2p\delta}\text{ ,}&\beta=p\alpha\in\left( \pi,2\pi \right) \end{cases}$

刚刚计算的磁动势和气隙磁场都只是通入时不变恒定电流在圆周上的空间分布，现在通入时变的交流电，电流变化为正弦式，峰值为 $\sqrt2 I$ ，平均值为 $I$ ，频率为 $\omega$ ，初相位为0

(8.7) $i(t)=\sqrt2 I \cdot cos(\omega t)$

那么现在的磁动势分布就不仅和角度有关，还与时间有关了

(8.8) $\Theta\left(\beta,t\right)=\begin{cases} +\frac{N }{p}\cdot i(t)\text{ ,}& \beta=p\alpha\in\left(0,\pi\right) \\ -\frac{N }{p}\cdot i(t)\text{ ,}&\beta=p\alpha\in\left( \pi,2\pi\right) \end{cases}$

这种“交变的磁动势”在时间上，总是在某确定空间角度上，按照正弦函数周期变化。而空间上的磁动势总是在某确定时间点，继续保持方形分布。

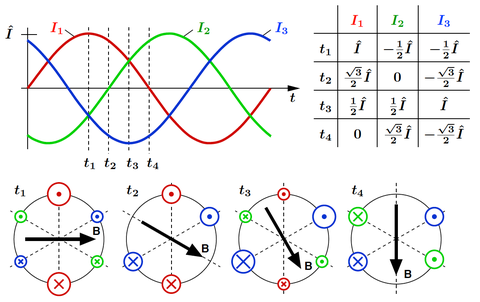
可见，随着时间增长， $\omega t$ 持续增大，而在每一段区间里的磁动势幅值大小开始按照正弦规律震荡(一个周期内，按照：”红色 $\to$ 蓝色 $\to$ 绿色 $\to$ 黄色 $\to$ 绿色 $\to$ 蓝色 $\to$ 红色“变化)。虽然时间上是简单的正弦函数，但是空间上却是难以简单描述的方波函数！如果不用分段函数，对这种非线性函数的处理是很棘手的，不能用基本初等函数直接描述。所幸我们知道，任何连续函数都可以用傅里叶级数展开表示，而在工程上，假定除了不连续点总是处处收敛的，那么这个同时包含时空二重变化的函数可以改写为

(8.9) $\Theta\left(\beta,t\right)=\left(\frac{N }{p}\cdot\sum_{g=1}^{\infty} \left\{\frac{4}{\pi}\cdot \frac{1}{2g-1}\cdot sin[(2g-1)\beta] \right\}\right) \cdot [ \sqrt2 I \cdot cos(\omega t) ],g\in N^{*}$

上式左边的傅里叶级数部分即描述了空间上的方波分布，而右边则为时间上的正弦分布。通过傅里叶级数展开可以获得一连串幅值和周期各不相等正弦函数，经过无穷次的叠加最终逼近了我们原本的方波函数！可以看到， $g=1$ 时幅值最大，周期最长(即出现频率最小)，我们把它称为基波(Grundwelle)， $g=2$ 时有频率为基波3倍的正弦函数，被称为三次谐波，以此类推。我们把基波以外的，频率更高的谐波统一称为高次谐波(Oberwelle)。

交变的磁动势可以用无穷个奇数阶谐波表示，为了方便，系数统一合写成幅值 $\hat \Theta_{2g-1}$

(8.10) $\Theta\left(\beta,t\right)=\sum_{g=1}^{\infty}\Theta_{2g-1}\left(\beta,t\right)=\sum_{g=1}^{\infty}\left\{\hat \Theta_{2g-1} cos(\omega t)\cdot sin[(2g-1)\beta]\right\}$

其中，基波为

(8.11) $\Theta_{1}\left(\beta,t\right)=\hat \Theta_{1} cos(\omega t)\cdot sin\beta=\hat \Theta_{1} cos(\omega t)\cdot sin(p\alpha)$

(8.12) $\hat \Theta_{1}=\frac{N }{p}\cdot \frac{4}{\pi}\cdot \sqrt2 I$

高次谐波( $g>1$ )为

(8.13) $\Theta_{2g-1}\left(\beta,t\right)=\hat \Theta_{2g-1} cos(\omega t)\cdot sin[(2g-1)\beta]$

(8.14) $\hat \Theta_{2g-1}=\frac{N }{p}\cdot \frac{4}{\pi}\cdot \sqrt2 I \cdot \frac{1}{2g-1}=\frac{\hat \Theta_{1}}{2g-1}$

注：以后会多次傅里叶展开，为了便于书写，均以幅值合写系数，幅值符号上会有" $\text{^}$ "，例如此处的基波磁动势幅值 $\hat \Theta_{1}$ 。

特别注意到，这些高次谐波构成的函数都是只在原地振动，即所谓的驻波。因为波的节点和波腹不随时间位移，其幅值大小和电流强度成正比。那么我们立刻可以联想到，驻波是两个波长、周期、频率和波速相同的正弦波相向干涉形成的。

使用积化和差公式可以分解正余弦函数的乘积

(8.15) $cos(x)\cdot sin(y)=\frac{1}{2}sin(y-x)+\frac{1}{2}sin(y+x)$

那么改写驻波部分

(8.16) $\begin{align*} \Theta_{2g-1}\left(\beta,t\right)&=\frac{\hat \Theta_{2g-1}}{2} \cdot \left\{sin[(2g-1)\beta-\omega t]+sin[(2g-1)\beta+\omega t]\right\}\\ &=\Theta_{2g-1}^{+}\left(\beta,t\right)+\Theta_{2g-1}^{-}\left(\beta,t\right) \end{align*}$

(8.17) $\Theta_{2g-1}^{+}\left(\beta,t\right)=\frac{\hat \Theta_{2g-1}}{2} \cdot sin[(2g-1)\beta-\omega t]$

(8.18) $\Theta_{2g-1}^{-}\left(\beta,t\right)=\frac{\hat \Theta_{2g-1}}{2} \cdot sin[(2g-1)\beta+\omega t]$

可见谐波成分中包含正向运动的谐波和反向运动的谐波，前者 $\Theta_{2g-1}^{+}\left(\beta,t\right)$ 称为正序电流(mitlaufende Welle)，后者 $\Theta_{2g-1}^{-}\left(\beta,t\right)$ 称为负序电流(gegenlaufende Welle)。正序电流和负序电流的幅值仅为原来驻波的一半。

时域上正弦振荡的磁动势总是可以分解成正序电流和负序电流。

就如上一章所提到的，一维正弦运动实为二维旋转的一维投影，所以正弦振荡的磁动势实为旋转的磁动势！当函数的零线穿越点和最值点随着波的匀速行进，我们就知道这个旋转磁动势的旋转角速度(Winkelgeschwindigkeit)。

定义正向电角速度 $\omega_{2g-1}^{+}$ ，因为方波幅值恒定，所以磁动势幅值 $\Theta_{2g-1}^{\pm}\left(\beta,t\right)=const.$ 为常数，空间上方波沿圆周的传播满足波动方程，即有匀速传播的关系，其传播速度为

(8.19) $\omega_{2g-1}^{+}=\frac{d\beta}{dt}\bigg|_{\Theta_{2g-1}^{+}\left(\beta,t\right)=const.}=\frac{\omega}{2g-1}$

以及正向机械角速度 $\Omega_{2g-1}^{+}$

(8.20) $\Omega_{2g-1}^{+}=\frac{d\alpha}{dt}\bigg|_{\Theta_{2g-1}^{+}\left(\alpha,t\right)=const.}=+\frac{\omega}{(2g-1)p}=\frac{\omega_{2g-1}^{+}}{p}$

(8.21) $\begin{align*} \Theta_{2g-1}^{+}\left(\beta,t\right)&=\frac{\hat \Theta_{2g-1}}{2} \cdot sin[(2g-1)\beta-\omega t] \\&=\hat \Theta_{2g-1}^{+}sin\{(2g-1)(\beta-\omega_{2g-1}^{+} t )\}=\hat \Theta_{2g-1}^{+}sin\{(2g-1)p(\alpha-\Omega_{2g-1}^{+} t )\} \end{align*}$

同样，对应的有负向电角速度 $\omega_{2g-1}^{-}$

(8.22) $\omega_{2g-1}^{-}=\frac{d\beta}{dt}\bigg|_{\Theta_{2g-1}^{-}\left(\beta,t\right)=const.}=-\frac{\omega}{2g-1}$

以及负向机械角速度 $\Omega_{2g-1}^{-}$

(8.23) $\Omega_{2g-1}^{-}=\frac{d\alpha}{dt}\bigg|_{\Theta_{2g-1}^{-}\left(\alpha,t\right)=const.}=-\frac{\omega}{(2g-1)p}=\frac{\omega_{2g-1}^{-}}{p}$

(8.24) $\begin{align*} \Theta_{2g-1}^{-}\left(\beta,t\right)&=\frac{\hat \Theta_{2g-1}}{2} \cdot sin[(2g-1)\beta+\omega t] \\&=\hat \Theta_{2g-1}^{-}sin\{(2g-1)(\beta-\omega_{2g-1}^{-} t )\}=\hat \Theta_{2g-1}^{-}sin\{(2g-1)p(\alpha-\Omega_{2g-1}^{-} t )\} \end{align*}$

综上所述，一个方波的交变磁动势，可以被视为无穷多对正向和负向旋转的正弦式旋转磁动势的叠加。

(8.25) $\Theta\left(\beta,t\right)=\sum_{g=1}^{\infty}{ \hat \Theta_{2g-1}^{+}sin\{(2g-1)(\beta-\omega_{2g-1}^{+} t )\} }+\sum_{g=1}^{\infty}\hat \Theta_{2g-1}^{-}sin\{(2g-1)(\beta-\omega_{2g-1}^{-} t )\}$

它的每对正负旋转磁动势的幅值和角速度随阶数增大而逐渐减小

(8.26) $\omega_{2g-1}^{\pm}=\pm\frac{\omega}{2g-1}$

(8.27) $\hat \Theta_{2g-1}^{\pm}=\frac{\hat \Theta_{1}}{2\cdot(2g-1)}$

##注意！##

在本文的讨论中，“振荡”(Schwingung)的概念只指的是，时间上的运动过程，例如在变频驱动电流的高频振荡 $cos( n\omega t)$ ；而“谐波”(Welle)的概念指的是，同时包括空间和时间上的变化，例如，旋转磁动势，它包含了 $sin(p\alpha+\omega t)$ 。

1.2三相绕组的旋转磁动势

在上一章里我们只是研究了一对槽对的定子上绕组产生的旋转磁动势，现在我们要继续推广到复杂一点的三对绕组在多对槽对上的定子的情况。

线圈边宽度等于极宽 $w_S=\tau_p$ ，极对极数为 $2p$ ，在每对极上三对空间上按照 $2p/3p$ 放置的槽对，三捆匝数均为 $N$ 的线圈束按每一极对 $\frac{N}{p}$ 匝数缠绕在槽上，槽缝无穷窄的定子。此时转子仍没被绕线，而且气隙宽度是恒定的。

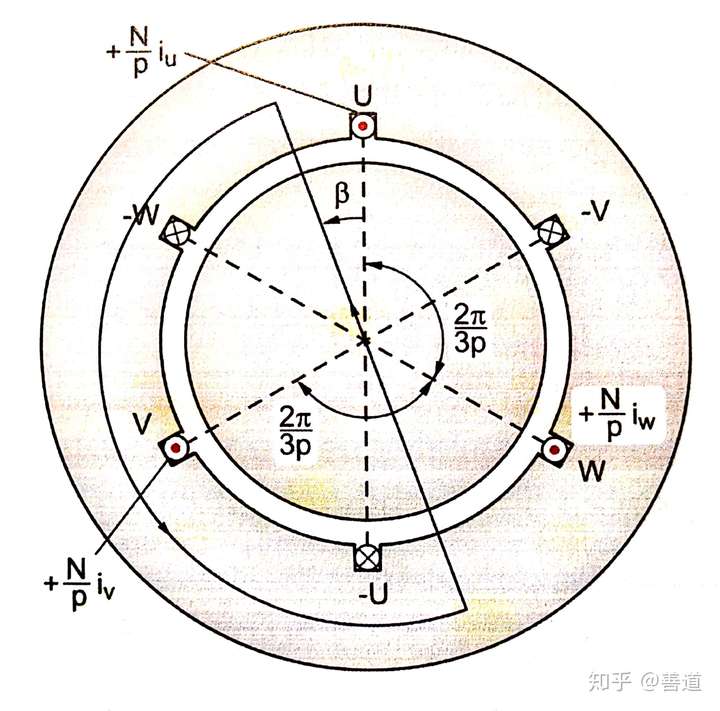
现在，三捆线圈束U,V,W通入两两相位差 $\frac{2\pi}{3}$ ，但幅值等大，峰值电流为 $\sqrt{2}I$ 的的同频正弦交流电，频率(电角速度)为 $\omega$ ，那么有

(8.28) $\begin{align*} i_U\left( t \right) & = \sqrt{2} I\cdot cos\left( \omega t \right)\\ i_V\left( t \right) & = \sqrt{2} I\cdot cos\left( \omega t -2\pi/3\right)\\ i_W\left( t \right) & = \sqrt{2} I\cdot cos\left( \omega t +2\pi/3\right)\\ \end{align*}$

那么每捆线圈束就生成了了对应的时间空间都在变动的交变磁动势

(8.29) $\begin{align*} \Theta_U\left(\beta,t\right)& =\begin{cases} -\frac{N}{p}\cdot\sqrt{2}I\cdot cos\left( \omega t \right),&\beta\in(0,\pi) \\ +\frac{N}{p}\cdot\sqrt{2}I\cdot cos\left( \omega t \right),&\beta\in(\pi,2\pi) \end{cases}\\ \Theta_V\left(\beta,t\right)& =\begin{cases} -\frac{N}{p}\cdot\sqrt{2}I\cdot cos\left( \omega t -\frac{2\pi}{3}\right),&\beta-\frac{2\pi}{3}\in(0,\pi) \\ +\frac{N}{p}\cdot\sqrt{2}I\cdot cos\left( \omega t -\frac{2\pi}{3}\right),&\beta-\frac{2\pi}{3}\in(\pi,2\pi) \end{cases}\\ \Theta_W\left(\beta,t\right)& =\begin{cases} -\frac{N}{p}\cdot\sqrt{2}I\cdot cos\left( \omega t +\frac{2\pi}{3}\right),&\beta+\frac{2\pi}{3}\in(0,\pi) \\ +\frac{N}{p}\cdot\sqrt{2}I\cdot cos\left( \omega t +\frac{2\pi}{3}\right),&\beta+\frac{2\pi}{3}\in(\pi,2\pi) \end{cases}\\ \end{align*}$

最后合成总的磁动势 $\Theta_S\left(\beta,t\right)$ 就可以把三捆线圈束上独立产生的交变磁动势线性叠加获得

(8.30) $\Theta_S\left(\beta,t\right)=\Theta_U\left(\beta,t\right)+\Theta_V\left(\beta,t\right)+\Theta_W\left(\beta,t\right)$

然而这种直接的线性叠加的前提假设是，与环路定理相关的计算都是线性的。所以再进一步的对磁感强度的线性叠加就不可实现了，因为铁芯会磁饱和抑或是气隙宽度不再恒定。

接下来仅考虑理想情况，磁动势可以线性叠加，使用傅里叶级数展开的正弦交变磁动势来求和以及表示

(8.31) $\begin{align*} \Theta_U\left(\beta,t\right)& =\hat \Theta_{1}\cdot cos\left( \omega t \right)\cdot\sum_{g=1}^{\infty}\frac{sin[(2g-1)\cdot\beta]}{2g-1}\\ \Theta_V\left(\beta,t\right)& =\hat \Theta_{1}\cdot cos\left( \omega t-\frac{2\pi}{3}\right)\cdot\sum_{g=1}^{\infty}\frac{sin[(2g-1)\cdot(\beta-\frac{2\pi}{3})]}{2g-1}\\ \Theta_W\left(\beta,t\right)& =\hat \Theta_{1}\cdot cos\left( \omega t+\frac{2\pi}{3}\right)\cdot\sum_{g=1}^{\infty}\frac{sin[(2g-1)\cdot(\beta+\frac{2\pi}{3})]}{2g-1}\\ \end{align*}$

基波幅值 $\hat \Theta_{1}=\frac{N }{p}\cdot \frac{4}{\pi}\cdot \sqrt2 I$ ，求和得到

(8.32) $\begin{align*} \Theta_S\left(\beta,t\right)&=\hat \Theta_{1}\cdot \sum_{g=1}^{\infty}\frac{sin[(2g-1)\cdot\beta]}{2g-1}\cdot cos\left( \omega t \right)\\ & +\hat \Theta_{1} \cdot\sum_{g=1}^{\infty}\frac{sin[(2g-1)\cdot(\beta-\frac{2\pi}{3})]}{2g-1}\cdot cos\left( \omega t-\frac{2\pi}{3}\right)\\ &+ \hat \Theta_{1} \cdot\sum_{g=1}^{\infty}\frac{sin[(2g-1)\cdot(\beta+\frac{2\pi}{3})]}{2g-1}\cdot cos\left( \omega t+\frac{2\pi}{3}\right)\\ \end{align*}$

运用积化和差继续分解

(8.33) $\begin{align*} \Theta_S\left(\beta,t\right)&=\frac{\hat \Theta_{1}}{2}\cdot \sum_{g=1}^{\infty}\frac{1}{2g-1}\left\{ sin[(2g-1)\beta-\omega t] +sin[(2g-1)\beta+\omega t] \right\}\\ &+\frac{\hat \Theta_{1}}{2}\cdot \sum_{g=1}^{\infty}\frac{1}{2g-1}\left\{ sin[(2g-1)\beta-\omega t-(2g-2)\cdot\frac{2\pi}{3}] +sin[(2g-1)\beta+\omega t-2g\cdot\frac{2\pi}{3}] \right\}\\ &+\frac{\hat \Theta_{1}}{2}\cdot \sum_{g=1}^{\infty}\frac{1}{2g-1}\left\{ sin[(2g-1)\beta-\omega t+(2g-2)\cdot\frac{2\pi}{3}] +sin[(2g-1)\beta+\omega t+2g\cdot\frac{2\pi}{3}] \right\} \end{align*}$

把其中正序电流部分全部相加，负序电流部分全部相加，注意到可以继续和差化积

(8.34) $\begin{align*} &sin[(2g-1)\beta-\omega t-(2g-2)\cdot\frac{2\pi}{3}] +sin[(2g-1)\beta-\omega t+(2g-2)\cdot\frac{2\pi}{3}]\\ &=2\cdot sin[(2g-1)\beta-\omega t]\cdot cos[(2g-2)\cdot\frac{2\pi}{3}] \end{align*}$

(8.35) $\begin{align*} &sin[(2g-1)\beta+\omega t-2g\cdot\frac{2\pi}{3}] +sin[(2g-1)\beta+\omega t+2g\cdot\frac{2\pi}{3}]\\ &=2\cdot sin[(2g-1)\beta+\omega t]\cdot cos(2g\cdot\frac{2\pi}{3}) \end{align*}$

把上式结论(8.34) (8.35) 代回原式(8.33) 则有

(8.36) $\begin{align*} \Theta_S\left(\beta,t\right)&= \frac{\hat \Theta_{1}}{2}\cdot \sum_{g=1}^{\infty}\frac{1}{2g-1}\left\{ sin[(2g-1)\beta-\omega t] \cdot \{1+2\cdot cos[(2g-2)\cdot\frac{2\pi}{3}]\}\right\}\\ &+\frac{\hat \Theta_{1}}{2}\cdot \sum_{g=1}^{\infty}\frac{1}{2g-1}\left\{ sin[(2g-1)\beta+\omega t] \cdot \{1+2\cdot cos(2g\cdot\frac{2\pi}{3})\}\right\} \end{align*}$

现在总的交变磁动势已经分为正向和负向旋转的磁动势，且以傅里叶级数形式表示，注意到由于正余弦周期性，不是所有项都能出现，有些项会周期性被消去，这显然取决于项数系数 $g$

(8.37) $(2g-2)\frac{2\pi}{3}=(g-1)\frac{4\pi}{3}=k\frac{4\pi}{3}$

那么可以再度消去那些为0的项，就可以进一步简化，对于正向旋转磁动势有

(8.38) $1+2\cdot cos(k\frac{4\pi}{3})= \begin{cases} 3,& k=3n,n\in N\\ 0,& else \end{cases}$

(8.39) $g-1=k=3n\Rightarrow g=3n+1,n\in N$

那么正向旋转磁动势的有效阶数为 $\nu$

(8.40) $\nu=2g-1=6n+1=1,7,13,19,...$

那么对于负向旋转磁动势有

(8.41) $g=3n,n\in N$

所以负向旋转磁动势的有效阶数为 $\nu$

(8.42) $\nu=2g-1=6n-1=5,11,17,23,...$

其他的阶数都被三捆线圈束上通的电流相互对消了，那么最后合成简化的三相绕组的磁动势为

(8.43) $\begin{align*} \Theta_S\left(\beta,t\right)&=\underbrace{ \frac{3}{2}\cdot\hat \Theta_{1}\cdot sin(\beta-\omega t)}_{基波}\\ &+ \underbrace{\frac{3}{2}\cdot\hat \Theta_{1}\cdot \sum_{n=1}^{\infty}\left\{ \frac{1}{6n+1}\cdot sin[(6n+1)\beta-\omega t] \right\}}_{正向旋转高次谐波}\\ &+ \underbrace{\frac{3}{2}\cdot\hat \Theta_{1}\cdot \sum_{n=1}^{\infty}\left\{ \frac{1}{6n-1}\cdot sin[(6n-1)\beta+\omega t] \right\}}_{反向旋转高次谐波}\\ \end{align*}$

当然，我们也可以把负向旋转磁动势的系数取负号( $n=-5,-11,-17,...$ )那么可以和正向旋转磁动势的级数合写在一起，同时令 $\nu=6n+1$ 则有

(8.44) $\Theta_S\left(\beta,t\right)= \frac{3}{2}\cdot\hat \Theta_{1}\sum_{n=-\infty}^{\infty}\left\{ \frac{1}{\nu}\cdot sin(\nu\cdot\beta-\omega t) \right\}$

其中基波为

(8.45) $\Theta_{S,1}\left(\beta,t\right)=\hat \Theta_{S,1}\cdot sin(\beta-\omega t)$

基波幅值为

(8.46) $\hat \Theta_{S,1}=\frac{3}{2}\hat \Theta_{1}=\frac{N }{p}\cdot \frac{6}{\pi}\cdot \sqrt2 I$

基波的机械角速度

(8.47) $\Omega_{1}=\frac{d\alpha}{dt}\bigg|_{\Theta_{S,1}\left(\alpha,t\right)=const.}=\frac{\omega}{p}$

其电角速度为

(8.48) $\omega=\frac{d\beta}{dt}\bigg|_{\Theta_{S,1}\left(\beta,t\right)=const.}=p\cdot\Omega_{1}$

对于高次谐波有，阶数 $\nu=6n+1=...,-11,-5,1,7,13,...$

(8.49) $\Theta_{S,\nu}\left(\beta,t\right)=\hat \Theta_{S,\nu}\cdot sin(\nu\cdot \beta-\omega t)$

(8.50) $\hat \Theta_{S,\nu}=\frac{3}{2}\hat \Theta_{1}\cdot \frac{1}{\nu}=\hat \Theta_{S,1}\cdot\frac{1}{\nu}$

对应的高次谐波的角速度分别为

(8.51) $\Omega_\nu=\frac{\omega_\nu}{p}=\frac{\omega}{p\cdot\nu}=\frac{\Omega_1}{\nu}$

(8.52) $\omega_\nu=p\cdot \Omega_\nu=\frac{\omega}{\nu}$

根据运算，我们发现高次谐波的旋转速度都要小于基波的，而且阶数越高越慢。正是各不相同的旋转角速度，导致了总的磁动势分布在每个时点，整体形状的扭曲失真。

1.3小结

在本章，我们详细讨论了三相交流电系统的定子上通入正弦交变会出现的可能的磁动势分布，我们发现这个交变磁动势的分布同时和时间空间有关，并且可以认为是驻波，并分解为正向旋转磁动势，以及负向旋转磁动势。并且得知还会衍生出无穷个高阶分量谐波电流，但是它们转动角速度随阶数增大而递减，导致了最后合成的波形的扭曲失真的可能性。

由于旋转磁场理论十分丰富，内容繁多，所以拆分成好几章，下一章继续探讨绕组因数的影响。

德国人怎么学电机——浅谈电机模型(八)：三相交流电机的旋转磁场理论(一)旋转磁动势

善道

前言

1旋转磁动势

1.1交变的磁动势的分布

1.2三相绕组的旋转磁动势

1.3小结

为你推荐

Arduino Uno 实验3——蜂鸣器

（指南者）（二）寄存器、定时器和中断

蓝桥杯嵌入式（G4系列）HAL：IIC通信之AT24C02与MCP4017

Arduino学习之一——软硬件准备

飞越650四轴无人机安装全程详解（多图）

树梅派4b+python+mlx90614

关于作者

善道

32

0

1

2

德国人怎么学电机——浅谈电机模型(二)：直流电机(一)机械构造和基本原理

德国人怎么学电机——浅谈电机模型(十七)：同步电机(四)永磁电机(二)

学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

相关推荐

Linux+QT+SocketCAN：使用信号槽机制实现数据收发

6、中断系统

stm32利用按钮控制LED灯（Develop文章1.2）

Arduino Uno 实验7——SG90舵机

精选嵌入式linux开发-（三）shell编程

基于51单片机的多功能智能语音循迹避障小车

热门泡泡

30积分失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

德国人怎么学电机——浅谈电机模型(八)：三相交流电机的旋转磁场理论(一)旋转磁动势

善道

前言

1旋转磁动势

1.1交变的磁动势的分布

1.2三相绕组的旋转磁动势

1.3小结

为你推荐

Arduino Uno 实验3——蜂鸣器

（指南者）（二）寄存器、定时器和中断

蓝桥杯嵌入式（G4系列）HAL：IIC通信之AT24C02与MCP4017

Arduino学习之一——软硬件准备

飞越650四轴无人机安装全程详解（多图）

树梅派4b+python+mlx90614

评论（0）

关于作者

善道

32

0

1

2

德国人怎么学电机——浅谈电机模型(二)：直流电机(一)机械构造和基本原理

德国人怎么学电机——浅谈电机模型(十七)：同步电机(四)永磁电机(二)

学习笔记：数值最优和模型预测控制(五)有约束静态最优化(一)带约束的最优条件

相关推荐

Linux+QT+SocketCAN：使用信号槽机制实现数据收发

6、中断系统

stm32利用按钮控制LED灯（Develop文章1.2）

Arduino Uno 实验7——SG90舵机

精选嵌入式linux开发-（三）shell编程

基于51单片机的多功能智能语音循迹避障小车

热门泡泡

30积分 失眠，聊聊自己搞ROS的心得体会吧

ros学习路线

30积分 TF_REPEATED_DATA ignoring data错误

各位大佬，有什么ROS定位算法推荐吗

5积分 想买能用ROS2的开发套件。或者开发板

5积分 ros中启动gazebo时报错

给作者打赏

忘记密码

修改头像

添加你感兴趣的标签

举报类型（必选）

举报详情（选填）

30积分失眠，聊聊自己搞ROS的心得体会吧

5积分想买能用ROS2的开发套件。或者开发板