目录
Fourier Series (傅里叶级数)
三角函数的正交性
周期为 2 π 2\pi2π 的函数展开为傅里叶级数
周期为 2 L 2L2L 的函数展开为傅里叶级数
傅里叶级数的复数形式
复数基函数的性质
Fourier Transform (FT, 傅里叶变换)
从时域到频域
傅里叶变换及其逆变换
参考文献
Fourier Series (傅里叶级数)
三角函数的正交性
可以定义一个内积空间,内积空间中的每个向量均为周期为 2 π 2\pi2π 的实值函数,函数之间的内积操作定义如下
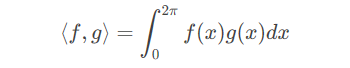
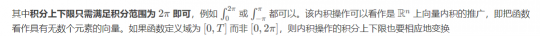

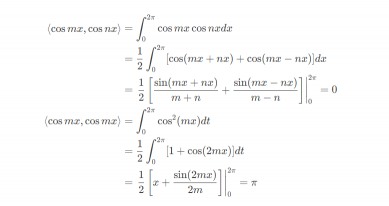
周期为 2 π 2\pi2π 的函数展开为傅里叶级数
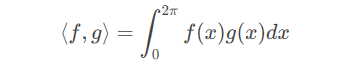
由于三角函数系是 C [ 0 , 2 π ] 的内积空间上的一组基,因此任何定义域在 [ 0 , 2 π ]上的连续函数均可以表示为三角函数的线性组合,下式即为傅里叶级数:
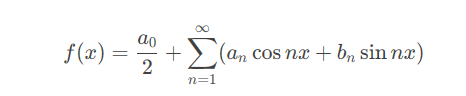
其中,a k , b k 为 f 的 Fourier coefficients. 傅里叶系数相当于是 f 在各个基向量上的投影,因此由正交投影可知,
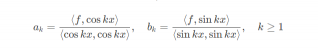
由于 ⟨ cos k x , cos k x ⟩ = π ,⟨ sin k x , sin k x ⟩ = π ,因此有
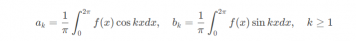
而 (constant) function 1 的傅里叶系数为
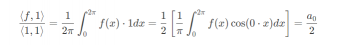
除了用投影的思想以外,也可以用如下方式求出傅里叶系数。例如,要求 a k 时,有
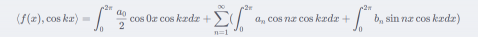
由三角函数的正交性可知,
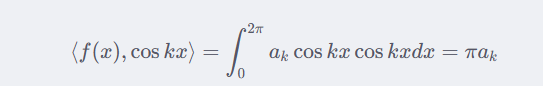
m mm 阶傅里叶近似即为

可以证明,当 m → ∞ 时,f 和傅里叶近似之间的均方误差也趋近于 0. m 阶傅里叶近似相当于是 f 在 { 1 , sin x , cos x , sin 2 x , cos 2 x , . . . , sin m x , cos m x } 张成的子空间 W WW 上的正交投影,并且由正交投影的线性性质可知

即 f + g的 m 阶傅里叶近似等于 f 的 m 阶傅里叶近似和 g 的 m阶傅里叶近似之和
EXAMPLE
Find the n nnth-order Fourier approximation to the function f ( t ) = t f(t)= tf(t)=t on the interval [ 0 , 2 π ] [0, 2\pi][0,2π].
SOLUTION
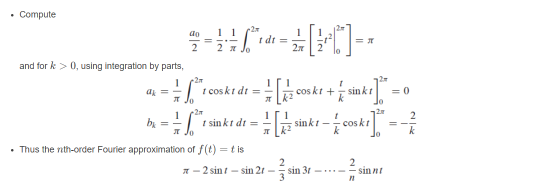
可以看到,三角函数频率越高系数越小,f ( t )的低频分量占了主要部分

周期为 2 L的函数展开为傅里叶级数
f(t)=f(t+2L)


因此,任何周期函数都可以看作是不同振幅,不同相位正弦波的叠加。在频域,0 频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状
傅里叶级数的复数形式

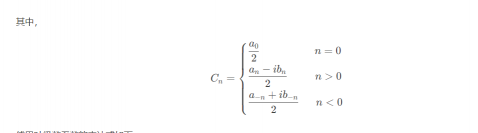
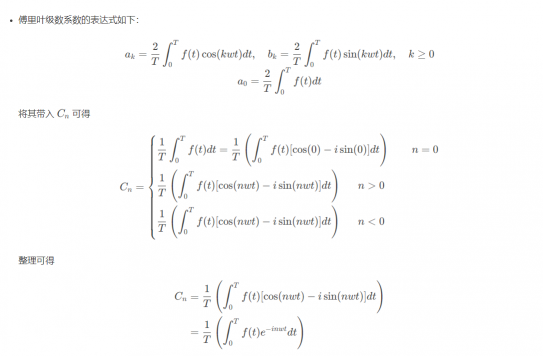
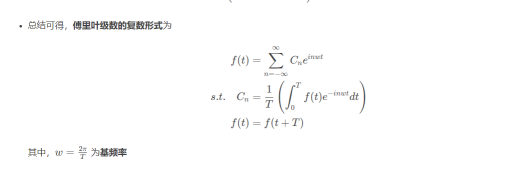
复数基函数的性质

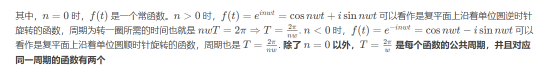

Fourier Transform (FT, 傅里叶变换)
从时域到频域

可以看到,区分不同周期函数的仅仅是 C n ,借此可以将一个周期函数从时域转换为频域:
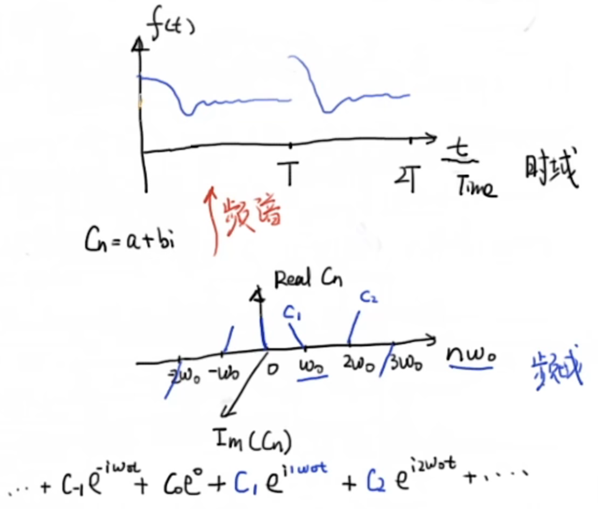
上图将 C n表示在了复平面中,实部和虚部都表示出来了 (振幅谱 + 相位谱)。但有时会将 C n 的幅度 ∣ C n ∣拿出来用以表示 f ( t ) 在不同频率下的强度 (振幅谱)
很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到;在图像处理领域,离散傅里叶变换将图像的离散像素数据转化为频谱数据,进行高频分量的舍弃与处理可以实现图像滤波以及图像压缩等目的
傅里叶变换及其逆变换
上面我们展示了周期函数时域到频域的变换,而非周期函数呢?将非周期函数由时域转换为频域的变换即为傅里叶变换。非周期函数可以看作 T → ∞ ,因此

也就是说,基频率 w 由离散变为了连续,周期函数频谱中横坐标离散的 n w 0 在非周期函数中就变为了连续的 w
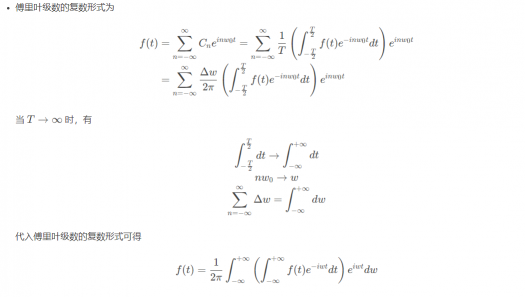
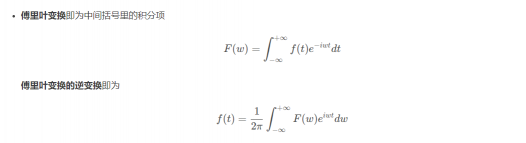
参考文献
纯干货数学推导_傅里叶级数与傅里叶变换
傅立叶变换夯实基础系列视频
linear algebra and its applications
傅里叶分析之掐死教程(完整版)






评论(1)
您还未登录,请登录后发表或查看评论