时间与运动
3.1轨迹
轨迹是具有特定时间属性的一条路径;轨迹的一个重要特征是平滑
3.1.1平滑一维轨迹
时间的标量函数:初始值和最终值确定,函数光滑
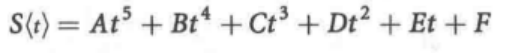
轨迹上定义了位置、速度和加速度的边界条件,一般情况下速度和加速度的边界条件均为零。
工具箱中的函数tpoly可以生成一个五次多项式轨迹:
>> s = tpoly ( 0, 1, 50 )
相应的速度加速度可以通过输出选项参数返回:
>> [ s ,sd, sdd ] = tpoly ( 0, 1, 50 )
速度和加速度分别为sd和sdd
多项式轨迹存在的一个问题:非零的初始速度导致多项式轨迹的中间值超过终点值。
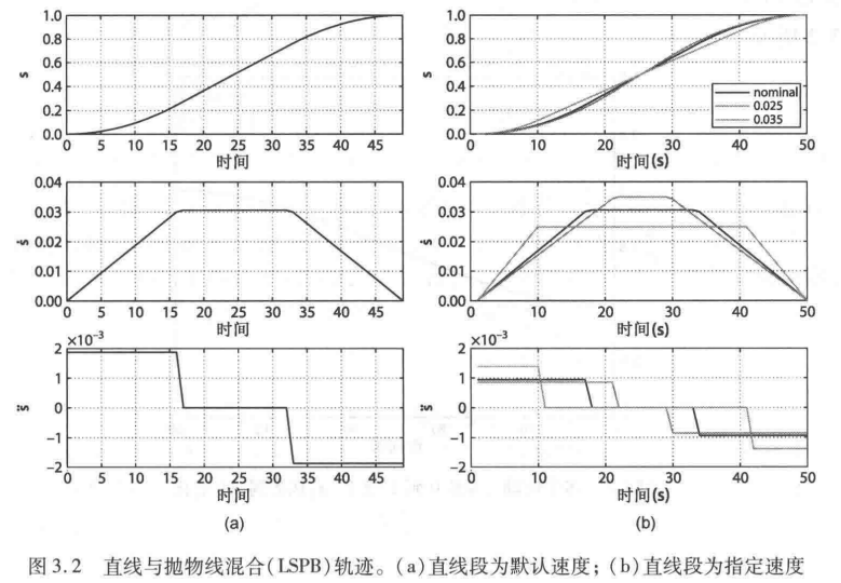
速度也是多项式轨迹一个很实际的问题,为了解决这个问题,一种公认的较理想的选择是采用混合曲线轨迹,即由中间的恒速段平直线加上两侧的加速段和减速段多项式曲线构成的轨迹。其混合轨迹是:
>> s = lspb( 0,1,50 )
轨迹由一条线段(匀速)与两条抛物线混合而成,得名lspb
这种类型的轨迹由于其速度-时间曲线的形状也被称作梯形轨迹,并普遍应用于工业马达驱动中。
3.1.2多维情况
向量形式xϵ![]() ,M表示自由度的数目。
,M表示自由度的数目。
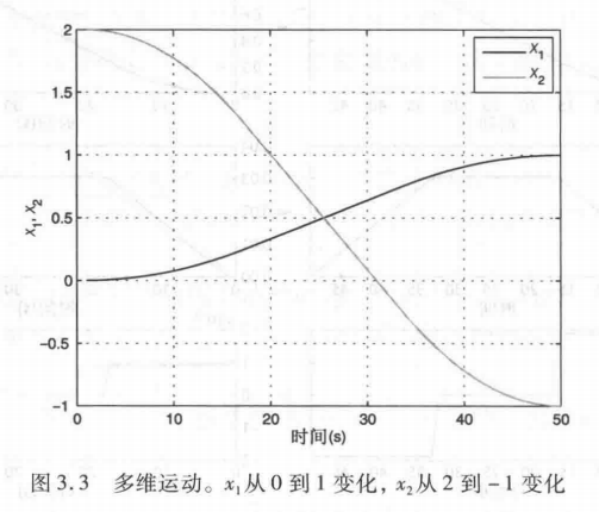
在工具箱中可以使用函数mtraj将平滑的标量轨迹扩展成向量。输入给mtraj的第一个参数是一个函数,即tpoly或lspb,它生成一个标量轨迹。以lspb为例,绘制其轨迹为
>> plot (x)
如图所示
3.1.3多段轨迹
为了使问题一般化,考虑该轨迹含有N个中间点xk, kϵ[1, N],因此有N-1个运动段。
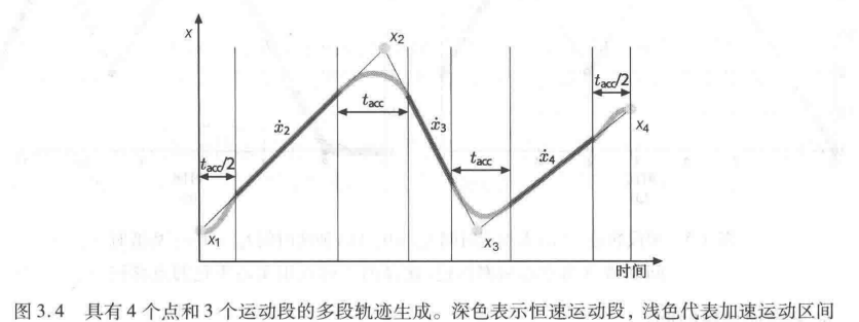
可以给每个直线段设定一个恒速值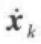 。因此,汇接混合中的平均加速度是
。因此,汇接混合中的平均加速度是
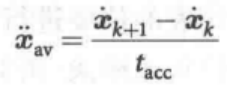 如果该轴的最大加速能力已知,那么就可以计算出最小混合时间。
如果该轴的最大加速能力已知,那么就可以计算出最小混合时间。
工具箱函数mstraj可以基于中间点矩阵生成一个多段多轴轨迹。函数mstraj的第一个参数是中间点矩阵,每点对应矩阵的一行。剩余的参数分别是:每轴的最大速度向量,每段的运动时间向量,起点各轴坐标,采样时间间隔,以及加速时间。
这个函数只是简单地对向量代表的位姿进行插值。
3.1.4三维空间姿态插值
一个可行且常用的选择是尝试三角度表示法,如欧拉角或横滚-俯仰-偏航角,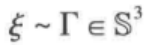 ,这样就可以使用线性插值法:
,这样就可以使用线性插值法:
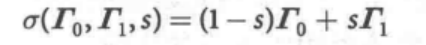
由于姿态变化较大,这个动作虽然平滑,但有时看 起来也不太协调。如果在所采用的三角度系统中有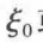 或
或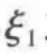 之一接近奇异点,也会出现问题。
之一接近奇异点,也会出现问题。
采用单位四元数的插值法在空间中产生一个绕固定轴旋转的姿态变化。利用工具箱函数找到与这两个位姿等价的四元数:
>> q0 = Quaternion(R0);
>> q1 = Quaternion(R1);
然后对它们进行插值:
>> q = interp(q0, q1, [0:49]'/49);
>> about(q)
q [Quaternion] : 1x50
得到一个有50个四元数对象的向量。
四元数插值法是通过使用球形线性插值(slerp)来实现的,其中单位四元数要在一个四维超球面上沿一个大圆路径运动。而在三维空间中的结果就是绕定轴的转动。
3.1.5笛卡尔运动
在SE(3)中生成两位姿之间的光滑路径,同时涉及位置及姿态的变化,通常被称作笛卡儿运动。
工具箱函数trinterp提供了沿路径单位化距离sϵ[0,1]中的位姿插值。
平移部分是用线性插值,旋转部分是用四元数插值法interp进行球形插值.
该轨迹的平移部分由以下方式获得:
>> P = transl (Ts);
位置向量的变化可以用plot函数画出:
>> plot(P);
工具箱中还提供了一个方便的速记函数ctraj来进行轨迹插值:
>>Ts=ctraj(T0, T1, 50);
其中的参数是初始和最终的位姿,以及分步数量。
3.2时变坐标系
3.2.1旋转坐标系
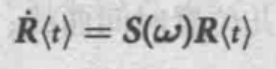
R<t>ϵSO(2)或SO(3),S(.)是一个斜对称矩阵,其三维情况下的具体形式如下:
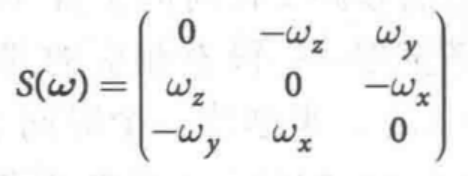
经过整理后可以得到方程:
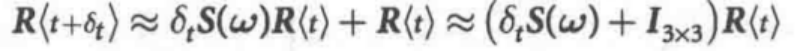
它描述了标准正交旋转矩阵是如何作为一个角速度的函数变化的。
3.2.2增量运动
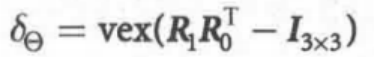
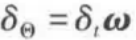 是一个三维向量,单位是角度,它表示一个绕世界坐标系的x,y和z三轴的无穷小转动。对于无穷小角度变化的乘法来说是可交换的。
是一个三维向量,单位是角度,它表示一个绕世界坐标系的x,y和z三轴的无穷小转动。对于无穷小角度变化的乘法来说是可交换的。
给出两个差异极小的位姿
如果位姿都用齐次变换矩阵的形式表示,那么位姿差异是
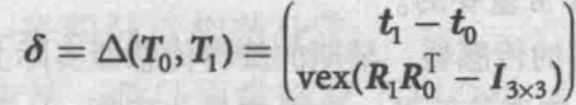
3.2.3惯性导航系统
惯性导航系统是一个“黑匣子”,用来测算它相对于惯性参考系(宇宙)的速度、方向和位置。
3个相互正交安装的陀螺仪可以测量出角速度w的3个分量,再使用方程
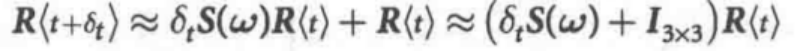
就可以不断计算出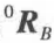 ,即固联于飞行器的坐标系{B}相对于恒星坐标系{0}的姿态。
,即固联于飞行器的坐标系{B}相对于恒星坐标系{0}的姿态。
以上方程的一种离散时间表达式为
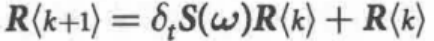
测出的飞行器坐标系加速度![]() 可以用下式旋转到惯性参考坐标系:
可以用下式旋转到惯性参考坐标系:
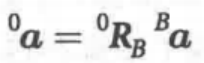
然后对它积分两次就可以得到在惯性坐标系中飞行器的位置。
工具箱中的规范化由以下函数实施:
>> T = trnorm(T);
单位四元数方法会使运算得以简化。其微分被定义为
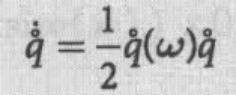
通过工具箱函数dot完成:
>> qd = q.dot(omega);
四元数变化率的积分通过下式获得:
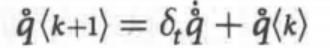





评论(0)
您还未登录,请登录后发表或查看评论