四、滚动控制
尽管优化向量ΔU包含了N c个控制变量序列，但是根据滚动控制原理，通常只使用这一序列中的第一个变量，即)Δu(k i )，忽略这一序列中的其余变量。当下一可采样周期到来时，使用新观测的状态变量x(k i​  +1)，重复以上优化过程，计算出新的控制变量序列，从而使优化窗口不断向前推进，每一采样时刻都进行实时预测与优化。

例：继续上例，一阶系统模型状态空间为：

考虑r_w=0的情况。初始条件为：

解：在采样时间k i = 10 时，上例已经计算出来的控制量为Δu(10)=7.2，因为u(9)=0，那么这一时刻的控制量 u(10)=u(0)+Δu(10)=7.2，y ( 10 ) = x m ( 10 ) = 0.2将这一时刻的控制量和状态量代入状态方程，可以计算下一采样时刻的状态变量为：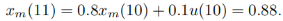

在采样时刻k i = 11，新的状态信息为Δ x m ( 11 ) = 0.88 − 0.2 = 0.68 ，y(11)=0.88，可以写成x ( 11 ) = [ 0.68 0.88 ] T ，可以得到新一轮的优化结果：

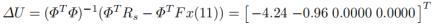
这一时刻的优化控制量为$u(11)=u(10)+\Delta u(11)=2.96$。使用这个控制量代入状态方程得到：

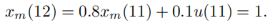
在采样时刻k i = 12 ，新的状态信息为Δ x m ( 12 ) = 1 − 0.88 = 0.12 ，y ( 12 ) = 1 ，可以写成x ( 11 ) = [ 0.12 1 ] T ，可以得到新一轮的优化结果：

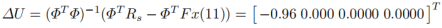
这一时刻的优化控制量为u(12)=u(11)+Δu(12)=2。使用这个控制量代入状态方程得到：

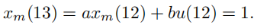
在k i = 13 3采样时刻，新的状态信息为Δ x m ( 13 ) = 1 − 1 = 0，y ( 13 ) = 1 ，可以写成x ( 11 ) = [ 0 1 ] T ，可以得到新一轮的优化结果：

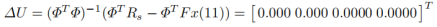
上述计算过程中，控制信号及状态变量如下图所示。

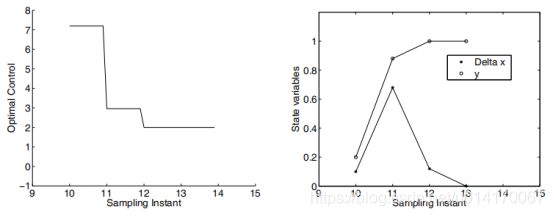
图2 控制信号、状态变化量和输出量曲线。这个例子还说明ΔU向量在不同时刻的的差异实例。注意，输出响应达到的设定点信号时，ΔU向量为零。

4.1 闭环控制

在k i  时刻，优化的向量参数ΔU通过下式计算：

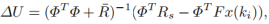
其中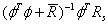

对应于期望输入的变化，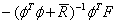

对应于状态反馈控制。全都取决于系统参数。因此在时不变系统中它们是常数矩阵。由于滚动控制中，只取ΔU中的第一个变量作为控制增量，因此：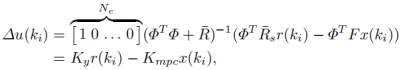

其中，K y 是下式的第一个元素：

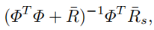
K m p c  是下式的第一行：

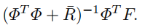
这是标准的时不变系统状态反馈控制。Kmpc​是反馈控制增益向量。代入增广矩阵当中得到闭环方程为：

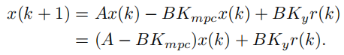
闭环特征值可以通过闭环特征方程得到：

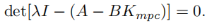
例1.5：求上例中产生的闭环反馈增益矩阵和权值r w = 0 和r w = 10 的闭环系统的特征值。
解：当r w = 0 时，

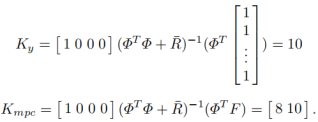
闭环系统的特征值由矩阵A−BKmpc​决定。从上例可知：

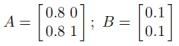
因此特征值为：

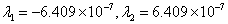
几乎在复平面的原点上。当r w = 100时，

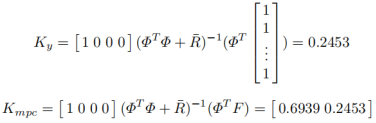
其特征值为：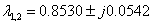

表明闭环系统的动力学响应比r w = 0时的响应要慢得多，这个结论也印证了之前例子中的分析。
例1.6：假设一个连续时间系统的传递函数如下：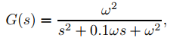

其中，ω = 10。用采样周期Δ t = 0.01将其离散化。当N c = 3 、R ˉ = 0.5I时，当参数N p = 20 和N p = 200 
时的参数敏感程度。
解：使用如下MATLAB函数将系统转换成连续时间状态空间模型：

omega=10;
numc=omega^2;
denc=[1 0.1*omega omega^2];
[Ac,Bc,Cc,Dc]=tf2ss(numc,denc);

得到连续状态空间方程为：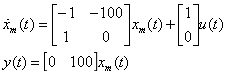

根据例1.1中的方法，得到增广状态空间方程为：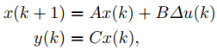

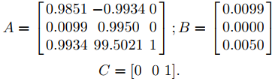
假设当前采样时刻为k = 10 ，初始条件为

当N p = 20时的Δ U为：

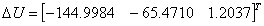
状态反馈控制增益为：

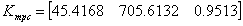
闭环特征值为：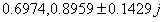

当时的为：N p = 200 时的为:

状态反馈控制增益为：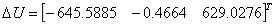

状态反馈控制增益为：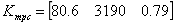

闭环特征值为：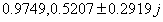

对比上述的求解结果可以看出，不同N p 对优化的控制变量ΔU影响巨大。这一比较研究说明了设计中控制变量ΔU关于的选择存在的敏感性。
仔细考察这一现象背后的原因，从研究海塞矩阵开始：

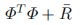
当N p $=20$时有：

其条件数为：

然而当N p = 200时有：

其条件数为：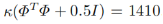

可以看出，当N p 由20增大到200时，海塞矩阵的条件数会剧烈增加，这就是导致控制量优化结果对参数N p 敏感度高的深层原因。
如果预测和控制周期较短，闭环预测控制系统不一定是稳定的。通常，这些参数是需要根据闭环控制稳定性和控制效果进行整定。后面会提出如何使用较长的预测和控制周期来确保闭环控制的稳定性。

4.2 Matlab实现

如何通过时域滚动控制方法在Matlab中实现模型预测控制？这是本教程想要达到的目的。假设系统的状态空间模型为：

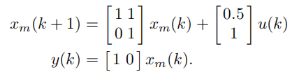
首先需要将系统模型和控制域长度N c、预测域长度N p 输入m文件。将上述二阶双积分系统，以及N c = 4 、N p = 4 输入到m文件，如下：

Ap=[1 1;0 1];
Bp=[0.5;1];
Cp=[1 0];
Dp=0;
Np=20;
Nc=4;

然后调用mpcgain.m文件中的函数得到增广模型矩阵，以及预测控制需要的各种矩阵。初始的状态变量为0，初始的状态反馈变量也为0，给定的期望输入为1，仿真采样个数为100，初始的控制量和输出量都是0：

[Phi_Phi,Phi_F,Phi_R,A_e, B_e,C_e] = mpcgain(Ap,Bp,Cp,Nc,Np);
[n,n_in]=size(B_e);
xm=[0;0];
Xf=zeros(n,1);
N_sim=100;
r=ones(N_sim,1);
u=0; % u(k-1) =0
y=0;

当采样时间为k时，向量ΔU根据期望输入r(k)和状态向量xf计算得到。控制量的增量只取ΔU的第一个元素，控制量为：

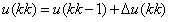
默认的权重系数为0.1。利用所产生的控制信号对系统的状态和输出进行仿真，得到的状态变量更新到变量xf中：

for kk=1:N_sim;
    DeltaU=inv(Phi_Phi+0.1*eye(Nc,Nc))*(Phi_R*r(kk)-Phi_F*Xf);
    deltau=DeltaU(1,1);
    u=u+deltau;
    u1(kk)=u;
    y1(kk)=y;
 
    xm_old=xm;
    xm=Ap*xm+Bp*u;
    y=Cp*xm;
    Xf=[xm-xm_old;y];
end
将系统输出、控制量曲线显示出来：
k=0:(N_sim-1);
figure
subplot(211)
plot(k,y1)
xlabel('Sampling Instant')
legend('Output')
subplot(212)
plot(k,u1)
xlabel('Sampling Instant')
legend('Control')

运行程之后的结果如下：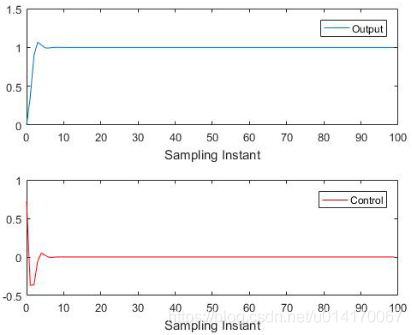

可以将权重系数修改到5做一下对比，可以发现，闭环响应速度会明显变慢：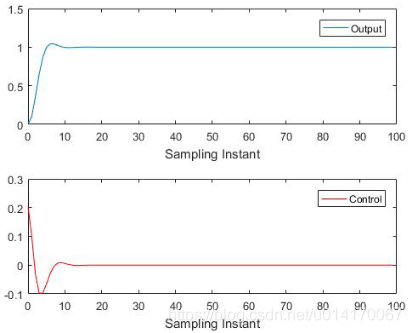

通过修改A p  , B p , C p 可以用来仿真其他系统模型，修改不同参数N p  , N c , r w来对比不同参数下的控制效果。

参考文献：
[1] Liuping Wang. Model Predictive Control System Design and Implementation Using MATLAB.