本节主要介绍最速降线问题，利用该问题来介绍分析力学发展的基础——变分法。

1. 最速降线问题

如图2-1所示，小球穿在光滑轨道上滑动，寻找使小球从  运动到  所需时间最短的路径  ，这就是所谓的最速降线问题。

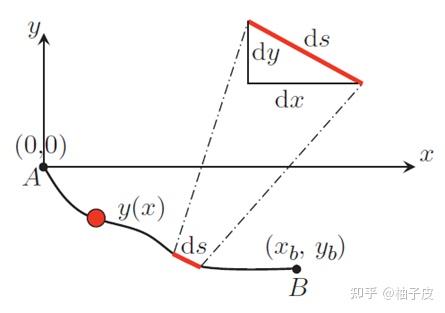
既然要求最速降线，我们就需要先将  与小球速度联系起来，已知

路程微分与时间微分存在关系：

注意到  ，则

不妨设  、  ，则需要的总时间  为

问题转化为了寻找使得上式取最小值的  。

解这个问题之前，我们先讨论更一般的情况：泛函的极值问题

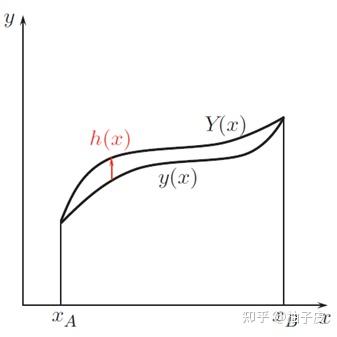
现在我们假设  为  稍加变化后的函数，两者有着相同的首尾，即、  ，如图2-2所示，有 。这样，我们可以得到解决问题的思路：对  求变分，计算出  时的  即为所求的  。

求一阶变分：

对上式使用分部积分法：

因为  ，因此上式等号右端第一项为零，故

考虑到  不恒为零，因此有

上式即为欧拉-拉格朗日方程，用来计算使得  取极值时的  。

接下来，我们利用这个方程处理最速降线问题，其中的  为

由于  不显含  ，因此

原本的欧拉-拉格朗日方程变为

因此有

即

将上式与  联立，得

故

因此解得

取  ，则  ，令  ，得  ；常数  则是由终端条件得到

已知  与  ，则可以解出  与  ，从而得到最速降线问题的解为如下参数方程：

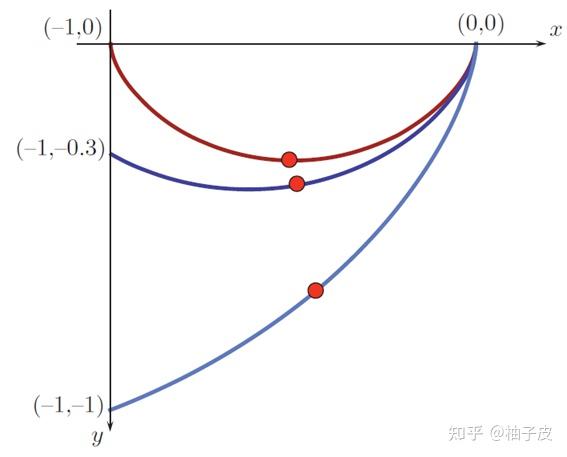
很明显，这是一系列的摆线，不同的终端条件形成的一系列的摆线如图2-3所示。

例2-1. 利用本节介绍的方法，证明两点之间线段最短。

解：要解决这个问题，我们需要证明，使得从  到  的距离最短的  是线性函数。距离微元为

两点之间的距离为

利用欧拉-拉格朗日方程，令  ，则

由于  、  ，因此

之前内容：

参考文献：F. Daqaq. Dynamics of particles and rigid bodies: a self-learning approach[M]. Hoboken, NJ: John Wiley & Sons, 2018.