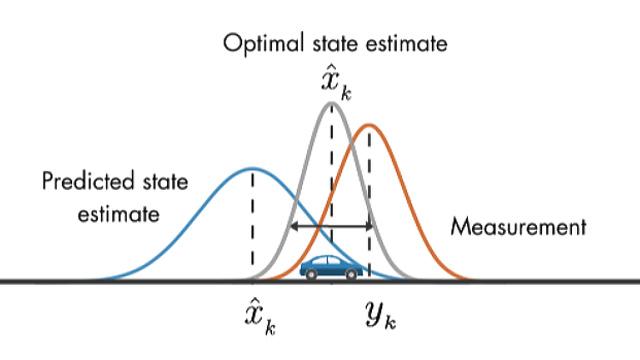
接下来的几篇从零开始介绍Kalman filter系列的文章花费了我许多时间整理。这个话题我一直不想开始讲，是因为真的要讲好这一块，并且从基础开始讲，是非常不容易的。这就是控制的难学之处，内容庞杂！ Kalman Filter既是控制设计方面学习者的需知常识，也是传感器系统设计和优化，信号处理，系统辨识等领域的实践者的必备知识。理解Kalman filter需要大概四块领域的知识：

1. 概率和随机过程理论(Probability and Random Process Theory)
2. 统计学和最优估计理论(Statistics and optimal estimation)
3. 信号处理 （Signal Proccessing）
4. 动力学系统常识(Dynamic Systems)

我会以5门本书的内容（见reference）为基础从最基础的知识开始讲，把必须知道的一些东西讲清楚，而不是上来便抛出一系列公式和符号。主要基于前4本书来讲解，第5本中文教材可以说是一个以上4本教材内容的一些简短总结。同样的，名词我会用中英文交替书写，以便你习惯以后阅读其他英文资料。

说是从0开始，你需要对控制和信号的基本知识有个大概了解。这一系列文章本来是作为LQG 控制(Linear Quadratic Gaussian Control) 的一点前奏，后来想好好写一写也算是给读者们的一点福利。由于filtering是一块非常庞大的知识体系，我只挑基础的必要知识来讲，以及基础的Kalman filter理论。Kalman filter有很多改进版本，这里作为关于控制的系列文章，我就不花时间列举了。作为现代控制理论系列文章的一块核心内容，但愿能帮助到你们学习控制理论。多点赞和推荐给你挣扎中的朋友，也算支持我抽空出来创作吧。

关于私信和咨询啊，做题写paper什么的术业有专攻，我就不回应这些诉求了。老实说很多知友抛出的问题我也不是一下子就能完全解答的，也得花费时间去找资料阅读和思考。我也没打算靠那点咨询费去赚钱，要的高了，知道很多人都是学生，也没那个经济能力。以我目前的工作状态，只能满足抽空来总结一些控制基础知识了，一方面是给自己的阅读留下一点笔记，另一方面给自己的一些要学习控制的学术界朋友和学生留点干货。我能保证的就是，既然写了，就一定要写好，不是截个图，连自己都没搞懂就来误人子弟。

本篇目录：

• What is Kalman Filter and its use? 卡尔曼滤波器和它的用途
• Why is Kalman Filter a Filter? 为什么叫 “滤波器”？
• Theory of Random Variable 随机变量理论
• Theory of Random Process 随机过程理论
• Theory of Signal Processing 信号处理理论
• Summary 小结

---

1. What is Kalman Filter and its use? 卡尔曼滤波器和它的用途

Kalman filter这个名字是以控制领域大神R. E. Kalman命名的一种滤波技术，或者说状态估计(state estimation)方法。如果不以他名字来命名，这个方法还可以叫做Linear Least-Mean-Squares Estimator（线性最小均方差估计），或者Linear Quadratic Estimator (线性二次型估计)[1,p1]。Kalman Filter的使用对象通常是一个线性随机系统(Linear stochastic system)，通过测量的含有随机噪音的输出来估计出最优的系统状态。这种最优性是建立在使得mean squared errors(MSE)最小的意义下，故有这两个名字。你可能还听说过Extended Kalman filter(EKF，扩展卡尔曼滤波器)，Adaptive Kalman Filtering(AKF, 自适应卡尔曼滤波）等等名词，先别着急，在把基本的知识介绍完后，再看也不迟。更多关于Kalman的一些事迹，将来有机会专门读些资料作为科普写一写。

Kalman filter的应用十分广泛，提供了可以真正实用的针对有限维随机系统的实时状态最优估计。它作为一种工具，主要有两方面的应用：state estimation 与performance analysis of estimation system[1,p4]。

1.状态估计(state estimation)： 我们之前讲过用Luenberger observer来估计线性时不变系统(LTI)的状态，那时候我们并没有考虑系统的输出中夹杂着的随机噪音的信息。注意！如果你看过我这个专栏之前关于观测器的文章，Luenberger observer是通过反馈的手段来抑制最后输出中的不确定性。我们知道在Luenberger observer的观测器方程中存在一个增益矩阵  ，与之相乘的是观测器输出与系统实际输出的差值。在Luenberger observer方程推导中我们并没有显示地去考虑噪音给我们带来的问题，而是把噪音的麻烦“下意识”地交给了反馈。采用反馈的目的就是抑制不确定性，那么噪音可以视为扰动，也就相对地会被这样的反馈设计所抑制。Kalman filter也干的同一件事：状态估计。因此Kalman filter也是一种observer。Kalman filter具有非常类似的结构，有预测值和实际观测值的参与去不断更新所谓的filter gain。filter gain是随着观测进行不断迭代而改变的，并不像Luenberger observer中的矩阵  往往是一个固定值。它们在噪音方面处理的主要不同是，Kalman filter的建模将noise的统计学信息作为已知信息考虑到了gain的设计中，而Luenberger observer却没有考虑噪音的任何信息。往往Luenberger observer的设计希望矩阵  都是相对准确的以达到最好的估计效果，而实际情况往往不如人愿。Kalman filter考虑了系统的动态过程中存在的随机性，更好地利用信息去完成系统状态的估计。

2.估计系统的性能分析(performance analysis of estimation system) : Kalman filter可以参数化表征其估计误差的大小，从而便于我们清楚是哪一个系统参数影响了最后的估计误差结果，这是有利于设计者分析估计系统的性能和提高估计精度的重要性质。比如采用的传感器种类，传感器位置，传感器带宽，噪音分布等等，都可以作为估计误差函数的参数。这种性质就可以帮助我们去做各个因素之间的权衡，指导我们去优化系统性能，而不是跟无头苍蝇一样trial and error。

2. Why is Kalman Filter a Filter? 为什么称之为 “滤波器”？

这是许多信号处理和控制的初学者经常问的一个问题：文献和书上总是出现filter或者filtering这个词的含义是什么？包括在computer science领域的imagine processing领域，我们也时常能看到各种滤波算法。

filter，原来的意思就是过滤器，或者俗称筛子。所谓过滤器，我们都知道，学化学或者生物的时候我们用来去处混合物中的杂质(impurities)用的。包括现在的很多净化产品，比如自来水过滤头，空气净化器本质上起到了的就是过滤作用。后来filter这个词被引入了信号处理领域，所谓的impurities在这个领域中往往是我们不想要的噪音(noise)分量。我们听过的低通滤波器(low-pass filter)，高通滤波器(high-pass filter)，带通滤波器(band-pass filter)，无论是数字的还是模拟的，都起到了滤除信号中不想要频率的作用。我在之前的专栏文章中也讲过，一个实际系统频响幅值越往高频走越小，信号输入系统后，其输出相当于通过了一个low-pass filter，此时该系统也可以被称为一个滤波器。这类对filter的理解，是“改变”了输入信号的频域信息，使得对应输出达到了我们想要的去除噪音的效果。 把噪音和filter的定义广义化，我们可以定义不同物理形式的滤波器。

不同于关注点在频率设计上的滤波器，Kalman filter和维纳滤波器(Wiener filter)采用了噪音和系统状态的统计学信息，一般以最小化mean-squared error（均方差）为优化目标，来给出原输入信号的最优估计(optimal estimation)，这个estimation的最优性(optimality)是以最小均方差为准的。Kalman filter和Wiener filter之间有各方面的差别，我们这里暂时不去细究。从实际应用上来讲，Kalman filter和它的改进版本由于适用于nonstationary process(非平稳过程)使用更加广泛。既然能够以某种最优标准还原信号，Kalman filter就拥有了一个与filter等同的功能：降噪(noise reduction)。这也是为什么Kalman filter被称之为所谓的滤波器的原因。

我们回过头来说，filter就是一类能够实现filtering的device或者algorithm。那么filtering又如何定义？[2,p10] 我们可以从两个方面去理解：

1. 使用可测量的信号，还原不能被直接测量或者带有噪音的信号。
2. 区别另外两种不同的信号处理方式：smoothing 和 prediciton

所谓的estimation就包含三种处理信号的方法：filtering（滤波），smoothing（平滑） 和 prediciton（预测）。在第二个层面的理解中，我们把filtering理解为：根据到目前时间  为止的信号的所有信息，来还原信号的部分或者全部信息。

Smoothing，所谓的信号平滑，并不要求只使用当前时间  之前的信息来估计真实信号，而是可以采用t之后的一段时间内的测量信号，返回来估计时间  的信号。简单说，我拥有了一段10秒长的信号，用10秒的信息回过头来过去信号在第5秒的值。这说明smoothing的估计并不是即时的，而是有一定的延迟(第5秒的信号估计，却延迟了5秒，等第10秒的信息得到后再得出。)。Smoothing是一块单独可以拿出来讲的内容，在这一系列中就不多做展开了。可想而知由于smoothing用到了更多的信息，理论上估计精度应该会更好。

Prediciton，信号预测就不用多说了吧？ 现在最火热的行业和研究领域莫过于AI了，其中的机器学习也好，深度学习也好，目标说到底是通过训练，代替人去做更好的预测。一般prediciton用到的信息就是截止到当前为止，然后输出是对未来的估计。

接下来我们会分几篇文章开始复习我认为比较重要的基础知识，为了后面理解Kalman filter的表达式做好铺垫。

3. Theory of Random Variable 随机变量

Hardcore的东西是避免不了的，不学基础理论，不分析过程，想要学会Kalman filter是不可能。即便后来你想要简单给别人讲个大概，你也要经历过这些基础又痛苦的过程才行！以下内容大部分都可以在[3]和[5]中找到，[5]的数学部分多是[3]的一些直接翻译。我挑点关键的列一列，剩下的如果用到了到时候再单独列出来。

概率的基础定义我就跳过了，多数人都可以通过简单定义理解。我们来说说随机变量(random variable)和随机过程(random process)的一些内容。随机变量  是一个定义在样本空间上的实值函数，把样本点映射成一个实数。每个样本点都有不同的概率出现，意味着随机变量的取值也是随机的，并且服从某个分布(distribution)。一个随机变量  的distribution是由 累积分布函数(cumulative distribution function,CDF)，或者简称distribution function来刻画的，是以一个实数为自变量的函数:

对于连续取值的随机变量，distribution function可以由概率密度函数(probability density functioin,PDF)，p(x)来表示：

他们两个之间的积分关系应该很容易理解。那么对于多个随机变量，我们可以定义联合积累分布函数(joint cumulative distribution function),

其联合概率密度函数(joint probability density function)  被定义为：

对于多元随机变量的情况，我们还可以定义marginal distribution function和marginal probability density function, 当我们只考虑其中一个随机变量时的分布时。

我们讲讲distribution的统计特性。随机变量最重要和常见的两个statistical measure就是数学期望(expected value)和方差(variance)。我们只说连续随机变量。一个随机变量的期望或者说均值(mean)的定义为：

其中  是  的概率密度函数。要指出的是，我们还经常把(5)叫做distribution的期望或者均值，所以这两种说法是一回事。  是随机变量或者分布的所有可能取值的概率加权，  的取值理应在这个  附近波动。而描述数据的波动性，我们采用方差，其定义如下：

之所以有(6)化简的结果，还要利用  ，因为理论上  是确定的。如果我们有一个随机变量的函数  , 那我们也可以定义上述期望和方差。我们也时常用  来表示expected value和variance。

一个随便变量  或者随机变量对应分布的矩(moment)是由如下积分定义的：

(7)称之为随机变量  关于实数c的k阶矩(The k-th moment of random variable X or distribution about a value c)。当  时，我们将结果称之为raw moment(原点矩)，当  时为中心矩(central moment)。矩的定义跟物理中的moment的定义是相同含义的，即表示物理量与对应距离乘积的积分，最常见的就是力矩了。矩就是一种综合考量了距离和量大小的量。根据(7)，我们发现所谓期望就是一个随机变量的first raw moment, 方差就是  或者对应distribution的second central moment。second raw moment是  的mean squared value:

定义root mean square(均方根，RMS)是：

一个随机变量的标准差(standard deviation)  被定义为方差的平方根，标准差的引入使得其值得量纲与均值是一致的，便于分析。一个随机变量的rms是其标准差，如果  。数学期望和方差实用的性质：

1. 
2. 若  独立，

协方差(covariance)是刻画二维随机变量  的两个分量之间相关性的一个特征数，由两个变量与其期望差值的乘积的期望定义：

当协方差大于0，则正相关，表示两个偏差同时增加或减少，反之则反方向变化。如果为0，则表示两个变量不相关，有可能是毫无联系，也有可能存在非线性关系。不相关(uncorrelated)和独立(independent)是两个概念，不相关比独立要更弱一些。如果两个变量是独立的，那么它们也是不相关的，则  。反之，却不一定成立。所以  成立的条件可以弱化为  不相关即可。

由协方差的定义我们可以计算：

为了消除协方差的量纲，引入取值在-1到1之间的(线性)相关系数(correlation coefficient)：

如果用向量和矩阵的形式来写  维随机向量的期望：

用协方差矩阵(covariance matrix)来记录随机变量各分量的协方差：

对角线上的协方差其实就是各分项的方差  。Covariance matrix有许多重要的应用，它是一个对称的，非负定矩阵(nonnegative definite matrix).

4. Theory of Random Process 随机过程

随机过程(Random process)是一个时间序列。它可以看成是一个随机变量簇 ，在每一个时刻  ， 都有一个独立存在于此时刻的随机变量 及其分布。在单独的某个时刻，它与之前讨论的随机变量无异。所以有无数个随机变量在相应的时间处取值，然后构成随机过程  。

我们也可以认为随机过程  是无数个时间函数的集合，随机过程的一个具体实现  就来自这个时间函数的集合。一个一般的随机过程在每一个时刻  的分布函数是一个时变函数：

概率密度函数为：

同样的可以定义二阶联合概率分布函数和密度函数表示两个时间点  处联合概率。一般随机过程的统计特征是随着时间而改变的：

有一类随机过程是很特殊的，对于任意选取的n个时间点  ，和一个任意延时 ，都有n阶联合概率密度函数：

则称随机过程  是stationary(平稳的)，或者strictly stationary。由于任意一段时间  内的联合概率密度函数不变，这意味着随机过程的各项统计特性都是保持不变的（前提是存在，可能有期望和方差都不存在的情况，比如满足柯西分布的平稳过程）。实际上这种假设只是理想的，按定义是难以验证的，实际中一般只能近似，严格说所有自然随机过程都是非平稳的(non-stationary)。工程中常见的是weak or wide-sense stationarity(WSS，弱平稳过程，或宽平稳过程)。所谓WSS random process，是指二阶矩  存在，均值是常数，且自相关函数(autocorrelation)仅与一个时间差  相关的random process。

一个实值随机过程的自相关函数(autocorrelation function, ACF)是由下式定义的：

对于WSS RP我们有autocorrelation：

同理也可以定义auto-covariance function以及两个随机过程之间的cross-correlation.

让我们考虑WSS的具体均值和自相关函数的计算。一般获得WSS的统计特性，需要重复多次试验，得到多条随机过程的实现  ，然后根据试验次数来求样本均值或者样本自相关值来近似真实值。但是重复增加试验次数，并不是一个好办法，我们就想如果只通过一个试验样本，但是加长时间，是否也能准确地去计算其统计特性。各态历经假说(ergodic hypothesis)指的就是一个宽平稳随机过程的统计特性，通过其全部可能的实现  的平均统计特性值计算的结果，与任意一个实现  在全部时间上求平均值得到的结果，是一样的。实际中几乎所有的宽平稳过程的统计特性都是基于ergodic hypothesis，通过一个试验结果来计算的。这里注意，我们讲宽平稳过程，而不是严平稳过程。对于一个严平稳过程，很难实际验证，并且其期望和方差都不一定存在，也就无所谓通过求时间均值的办法来逼近了。

用公式来表明可能会更加容易：公式(16)计算均值的方法是一种理论上可以计算WSS均值的办法，这是将每一个时刻的随机变量与其概率相乘再积分的办法；我们还可以理解一个随机过程  是所有可能实现的集合，所以均值也就是同一个时间段内的不同可能实现的  的时间均值，我们可以根据下式来计算其均值：

当然只是理论上的，一方面同一个时间段理论上只能得知一个实现  (不可能时间倒流回去再得到同一段时间内的另外一个实现)，另一方面实现的数量也只能是有限的。实际操作中，实际只能取有限个试验序列来近似。ergodic hypothesis告诉我们均值也可以通过时间均值来计算：

即同一个试验序列的均值只要时间够久也能收敛到  。其他的统计特性同理，比如WSS的自相关函数我们可以根据下式计算：

以下有一些别的回答和wikipedia供参考：

5. Theory of Signal Processing 信号处理理论

信号处理(Signal Processing)作为一门基础课，属于还比较难的。我们挑选一点概念在这里讲讲，我会给出一些简洁易懂的reference，便于读者扩展阅读。

接触过信号处理的话，你上来可能就听说过两个词: 功率信号(power signal)和能量信号(energy signal)。上来我们可以直接把这两个词的定义给背一遍：

energy signal就是指信号具有有限的能量，在无穷时间中其平均功率为0。

power signal是功率有限的信号，在无穷时间中的积累表明其具有无限的能量。

要理解上述定义，我们首先定义signal processing中信号的能量(energy)：

这与物理学中的能量并不一样，但是却有联系。如果是电压信号，那么(24)计算的能量量纲是  ，而电路理论中能量的单位是  。

有了能量的概念，我们可以顺势定义一个信号的功率，大概想想是能量与时间的比值。问题是(23)中定义的能量是在无穷时域中定义的，这时候我们要问，是否有些信号的能量根据(23)计算是有限的，或者是无限的。如果根据(24)我们发现一个信号在无穷时域中的  ，那么这个信号就是energy signal。对于一个连续时域信号，在无穷时间内的平均功率为：

对于energy signal，显然无穷时间内的平均功率为0。那么如果一个信号的能量理论上是无限的，(24)的分子是无穷的，分母也趋向于无穷，最后平均功率又会什么呢？如果分子的发散速度比分母快，那么其平均功率会无穷大时；如果分母发散更快，则平均功率为0；如果发散速度在无穷时域内基本都能保持的差不多，最后平均功率会有界。如果一个信号在无穷时域上的能量理论上是无穷的，并且其平均功率是有限的，我们就称这个为功率信号,power signal。问题来了，哪些信号是功率信号呢？

周期信号是功率信号。假设时间为  ，  是周期信号的周期，那么(25)就成为了：

现实中的周期信号，在周期区间上分母都是有界的，很明显(26)最后的结果一定是有界的，所以一般周期信号是功率信号无误。

宽平稳随机信号也是功率信号。一般的随机信号是不一定满足能量无限且(24)有界的。我们这里考虑满足各态历经假说的宽平稳随机信号。如前所述，它的统计量是可以通过单一信号在无穷时域中的平均值来逼近的，如同(22)的WSS process那样。在各态历经假说成立的情况下，我们知道宽平稳随机信号的二阶矩存在，均值为常数，并且可以通过时间均值来计算：

由于  是一个常值，所以我们可以断定  是有界的，我们把这个一个信号的  叫做均方值(mean squared value)。一般宽平稳随机信号满足ergodic hypothesis，我们就有均方值： 很明显这就是平均功率的定义，所以我们说此满足WSS过程定义的信号是一个功率信号。而均方值的平方根，正是RMS，工程上常称之为有效值(算交流电的有效值时我们碰到过这个概念)。如果WSS信号均值为0，那么信号的平均功率根据(27)就是其方差。

我们关注功率信号，因为我们通常把采集到的随机信号认为是功率信号。根据帕塞瓦尔定理(Parseval theorem)，时域信号的能量与频域内该信号的能量相等：

对于能量信号，我们可以定义  为能量谱密度(energy power density)来描述信号能量在各频率上的分布。对于功率信号，我们要采用功率谱密度(power spectral density, PSD)，或者自功率谱、自谱，来描述其平均功率的在频域上的分布。我们把平均功率转换到频域中：

这里的  就是自谱。至于说到底频率的单位是Hertz还是radian，这个看单位，并不关键。随机过程有很多个可能的实现，它的统计平均功率谱密度是  。根据Wiener–Khinchin theorem, 我们知道宽平稳随机过程的PSD与其自相关函数是互为傅里叶变换的：

实际中自相关函数是可以获取的，所以可以通过这层关系来估算WSS过程的自谱。实际中PSD只能通过一段截短的信号来估算，在MATLAB中有一些函数可以提供估算结果，叫periodogram，有专门的算法。最常见的估计PSD的方法是Welch's method，见MATLAB参考。以下是一点额外的参考资料：

白噪声(white noise)一种理想的随机信号，其功率谱在所有频率中是一个非零常数。如果功率谱不是一个常值，却也在全频率分布，被认为是噪声的信号，我们称之为有色噪音(colored noise)。白噪音是  的power spectral density定义为常数：

由于自相关函数的Fourier变换是功率谱密度函数，所以我们知道白噪音的autocorrelation function  为：

其中  是Dirac函数。因为Dirac函数在原点处无穷大，我们就知道白噪声的幅值只有当  时才与自身相关，而其他任何时候各时刻幅值均不相关。由于功率谱无限宽，其带宽也是无限宽的，现实中无法实现，但是现实中常会把一些信号近似为白噪声去研究。所谓“白”色，也是由于白光含有所有频率的不同单色光得名。

注意，在这个白噪声的定义中，我们没有给白噪声的幅值赋予任何的概率分布。如果我们认为白噪音是independent，identically distributed(iid)，那么白噪声是一个理想的平稳过程。很多定义默认白噪音是一个平稳过程，我曾经也为定义的问题而困惑。不过后来觉得纠结定义什么的并不重要，从实际角度看，我们最终要处理都要把实际信号当作宽平稳状态过程，即WSS process。有很多定义方面的东西，如果你仔细去思考，你会有很多疑问。很多版本的定义并不能完全把一个东西与另外一个东西区别开来。但死磕这类有工程背景学科的定义会浪费很多时间，相比于严谨科学-数学，我们要从更实际的角度去理解这些定义。

当白噪声通过一个线性系统后，输出便成了有色噪声，即其功率谱不是一个常数，而是随着频率改变发生衰减。对应输出的autocorrelation function也成了一个指数函数，随着  的增加而衰减[5,p50]。这再次表明了一个实际线性系统相当于一个low-pass filter。

白噪声本身并没有暗示任何概率分布。现实中噪音的概率分布是不容易得到的。假设一个环境中各个噪音源是独立分布，且来自同一个分布，并且噪音源数量很大，根据中心极限定理(central limit theorem)，噪音源的总和也是一个随机变量，并且服从正态分布(Gaussian distribution, or normal distribution)。那么现实中在信号处理的问题中，热噪声(thermal noise, or Johnson–Nyquist noise) 是一种基本的噪音，是由于电子热运动造成的。考虑到电子数量众多，它们共同作用下产生的噪声的概率分布可以认为是Gaussian distribution，而且其功率谱密度不随频率变化而变化，这就是为什么我们可以假设一般噪音是白噪声，并且服从Gaussian distribution的原因之一，这也是处理复杂问题的一种简单有效的方法。如果一个白噪声幅值服从Gaussian distribution，假设其满足各态历经性，那么我们就把它称为高斯白噪声(Gaussian white noise,or additive white Gaussian noise, AWGN)。理想的AWGN是一种平稳的随机噪声(分布不随时间改变)，其均值  ，方差为  。由于均值为0，我们根据方差的定义：

此时方差就是均方值。由于是各态历经的，我们考虑(28)得知，一个均值为0的信号的均方值就是其平均功率，由此推知AWGN的平均功率是无穷大的，即方差无穷大，理想的AWGN根本无法实现（power spectral density仍然是常值，代表的是单位频率上的功率值）。那么为了实现所谓的AWGN，我们必须使其的带宽是有限的，即只有在一段频率上功率谱密度保持常值，这样其自相关函数在  处的取值便为有限值，即平均功率为有限值，实际的正态分布方差是有限的:

根据(35)的带限白噪声(bandlimited white noise)，我们根据自谱与自相关函数的关系：

(36)在  时的极限值是一个有限值。根据(34)，我们便知bandlimited gaussian white noise的二阶矩（此处即方差，或者平均功率）是一个有限值，均值为常数0，并且其自相关函数仅与时间  有关，这符合我们工程中常处理的宽平稳过程，即WSS信号的定义。回过头去看，理想的高斯白噪声由于平均功率无限大，即二阶矩不存在，并不符合WSS的定义。

一个随机过程可以认为有无数个随机变量组成，如果其中任取任意数量的随机变量组成向量，它们的联合概率分布都满足Gaussian distribution，那么这个过程就是高斯过程(Gaussian process)。上面的高斯白噪声，我们假设的是所有噪声源都是独立同分布的(independent and identically distributed)，根据中心极限定理，随机变量的和  最后是呈正态分布的。由于是平稳信号，在每一个时刻  ，  也服从同一个Gaussian distribution的，我们说高斯白噪声就是一种高斯过程。如同一维正态分布只取决于均值  和方差  ，高维正态分布取决于均值向量和协方差矩阵。

关于高斯白噪声的均值，我看了很多定义，我认为均值为0是人们给出的，也符合现实中噪音的统计规律。在[5,p53]中这位作者的一些推导让我产生了困惑。我们知道理想的AWGN的自相关函数只有在  时是无穷大的，其余处均为0，因而：

随后这位作者表明  因为白噪音的自相关函数表明2个时刻的噪声不相关。但是  是根据协方差  得出的，只有  我们才能说这两个变量是“不相关的”，这样才有  ，从而表明高斯白噪声的  ，即均值为0。不过另外一种理解是，我们主观上已经认定  就是独立的，或者弱点说就是不相关的，无需公式去证明，那么在这个假定下，我们自然就能推知高斯白噪声的均值为0。无论是哪一种思路，均值为0都是我们事先给定假设的结果。这一点请读者思考，如果有想法请告诉我。

以下是一点知乎上的参考资料，可供参考：

一阶Markov过程  的下一时刻的概率分布只与上一个时刻的概率分布有关，而与过去的其他时刻的概率分布无关，或者说现在的概率分布和过去所有的概率分布对下一时刻的影响与现在的概率分布对其影响等效。一阶Markov process可以由一阶微分方程，且输入为white noise表示[3,p42][5,p53]：

如果白噪声是AWGN，那么输出  为Gauss-Markov Process. 一阶Gauss-Markov process有指数型autocorrelation function [see 5,p53]  ，其中系数  的值趋向于0，相当于截断频率越来越低，输出会趋向于随机常数；随着  增加，一阶系统带宽增加，所以输出的频率也变宽，越来越接近白噪声。同理我们可以定义二阶Gauss-Markov Process，详细请参考[3,p42-p45]和[5,p53]。需要用到时，我们再细说。

随机游走(random walk)是将白噪声通过积分器后得到的随机过程：

随机游走的期望  根据定义为0，自相关函数是与起始时间有关的[5,p56]，输出非平稳过程。

6. 小结

基础理论这篇文章就先讲到这里，我们回顾了随机变量，随机过程和信号处理的一些重要概念，前面也提到了Kalman filter的一些常识。Kalman filter最重要的功能就是状态估计，在控制中我们也都碰到过状态估计问题。上面这些基础知识，一定要反复学习，多查权威资料，多读多思考，理解它们的含义。概率论和信号处理，绝对是两门相当难学的课程，我想经历过学习的朋友都应该深有体会。但是无奈Kalman filter相关的知识就必须要精通很多概念。

基础还远远没完，下一篇我会继续把线性系统中一些关键部分以及最小二乘法和其它最优算法做一个回顾总结。争取第三篇我们开始讲Kalman filter的时候，诸位都能看明白。

Reference

[1] Grewal, M. S., & Andrews, A. P. (2015).Kalman filtering: Theory and Practice with MATLAB Fourth Edition. John Wiley & Sons.

[2] Anderson, B. D., & Moore, J. B. (1979).Optimal filtering. Prentice-Hall, Englewood Cliffs, New Jersey.

[3] Gelb, A. (1974).Applied optimal estimation. MIT press.

[4] Musoff, H., & Zarchan, P. (2009).Fundamentals of Kalman filtering: a practical approach. American Institute of Aeronautics and Astronautics.

[5] 王可东(2019).Kalman滤波基础及MATLAB仿真，北京航空航天大学出版社.