1. 引言

  前面文章已经介绍了机器人动力学基础以及牛顿欧拉法推导机器人动力学。这篇文章介绍拉格朗日法推导动力学的过程。
  牛顿欧拉法和拉格朗日法求解动力学方程出发点是不同的。在牛顿欧拉法中因为我们曾经熟知牛顿第一和第二定律，因此它的难点主要在于各个连杆的速度，加速度等如何在连杆坐标系中表达出来。反观拉格朗日法，这种方法思路十分的直观和简单，它的难点在于我们难以接受其中的数学概念，比如广义坐标，广义力。再比如为什么拉格朗日方程是合理的等等。这篇文章将给出一种简单直观的解释。

2. 拉格朗日方程

2.1 直观理解

  对拉个朗日方程进行严格的证明是十分困难的一件事情，同时这种事情意义也不大。对于工科生而言最关键的还是对公式建立直观地认知。所以我们可以从一个简单的例子出发推导一下拉个朗日方程与牛顿第二定律的等价性。如下图1所示平面上放有一高度为h的桌子，桌子上表面光滑，小滑块在桌面上滑动，所受合外力为f，当前速度为v。我们可以根据以上提供的条件列出小滑块的拉格朗日方程。

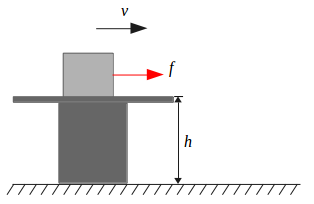
图1 小滑块的运动

  先来看滑块动能，根据动能定理小滑块的动能为：

E=\frac{1}{2}mv^2

以水平面为零势能面（向上和向右为正方向），重力加速度向下因此为-g，其中g=9.8m/s^2。因此滑块重力势能为：

U=mgh

则拉格朗日函数为：

L=E-U=\frac{1}{2}mv^2-mgh

由于小滑块只沿着水平方向运动，因此只需要一个坐标x(水平方向位移)就能描述它的运动，广义坐标的个数为1，f就是滑块所受广义力。因此小滑块的拉格朗日方程为：

\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{x}}\right)^T - \left(\frac{\partial L}{\partial x}\right)^T=f

由于这里都是一维运算因此转置符号可以去掉，将上面的式子展开可以得到：

\frac{d}{dt}\left(\frac{\partial L}{\partial v}\right) - \left(\frac{\partial L}{\partial x}\right)=f

先来看\frac{\partial L}{\partial v}，拉格朗日函数中只有动能部分和v有关，势能部分偏导后为0，因此：

\frac{\partial L}{\partial v} = mv

因此\frac{d}{dt}\left(\frac{\partial L}{\partial v}\right) =\frac{d}{dt}\left(mv\right)=ma。由于拉格朗日函数中的所有项都和广义坐标x无关，因此\frac{\partial L}{\partial x}=0。综上所述，小滑块的拉格朗日方程为：

\frac{d}{dt}\left(\frac{\partial L}{\partial v}\right) - \left(\frac{\partial L}{\partial x}\right)=ma=f

因此对于小滑块来说所谓拉格朗日方程就是牛顿第二定律！

2.2 小结

  上面推导了拉格朗日方程和牛顿第二定律是等价的，其实是从不同的角度出发来解决相同的问题，就像高中时候我们求解立体几何问题可以用几何法也可以用解析法一样。

3. 二连杆平面臂拉格朗日方程

3.1 任意刚体的动能和势能

  在介绍二连杆平面臂的动能和势能之前我觉得有必要介绍一下给我们任意一个刚体应该怎样求取刚体的动能和势能。如下图2所示是任意一个刚体，坐标系{O}为基坐标系（参考坐标系），图中所有的变量都是在这个坐标系中表达的。我们可以先来求刚体的动能。可以把刚体划分为一个个体积微元，先求解每一个体积微元的动能，再把他们加起来就是整个刚体的动能了。

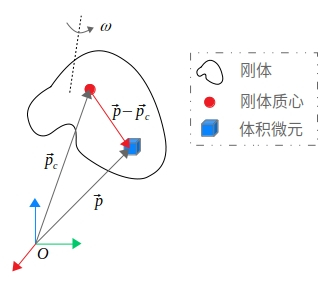
图2 任意刚体动能和势能

  以图2中任意一个体积微元为例，它的位置矢量为\vec{p}。\vec{p}_c为刚体质心位置矢量。设\vec{r}=\vec{p}-\vec{p}_c(为了方便，后面的公式中省去箭头)。那么体积微元的速度可以表达为：

\dot{p}=\dot{p}_c+\dot{r}=\dot{p}_c + \omega \times r

因此刚体的动能可以表达为如下积分形式：

E=\int_V \frac{1}{2}\dot{p}^T\dot{p}\ \rho dV=\frac{1}{2}\int_V \left(\dot{p}_c + \dot r\right)^T\left(\dot{p}_c + \dot r\right)\ \rho dV

把以上式子展开可以得到：

E=\frac{1}{2}\int_V \left(\dot{p}_c^T\dot{p}_c + 2\dot{r}^T\dot{p}_c + \dot{r}^T\dot{r} \right)\rho dV

由于\dot{r}=\omega \times r上式进一步展开得到：

E=\frac{1}{2}\int_V \left(\dot{p}_c^T\dot{p}_c + 2\left(\omega \times r\right)^T\dot{p}_c + \left(\omega \times r\right)^T\left(\omega \times r\right) \right)\rho dV

分开来看被积函数的三项\dot{p}_c本身对于积分变量dV来说是定值，因此：

\int_V \left(\dot{p}_c^T\dot{p}_c\right)\rho dV=\dot{p}_c^T\dot{p}_c\int_V\rho dV=m\dot{p}_c^T\dot{p}_c（质量乘以质心速度的平方）

角速度\omega对于积分变量来说也是定值（刚体任意位置角速度相等），因此：

\int_V2\left(\omega \times r\right)^T\dot{p}_c=2\left(\omega\times\int_V r\ \rho dV\right)^T\dot{p}_c=2\left(\omega\times0\right)\dot{p}_c=0

这个地方跨度有点大，用到的原理：
1.叉乘是满足分配律的，积分本质上是求和运算，因此角速度\omega可以提到积分符号外面。
2.向量r体积分为0原因是向量r起点为质心，而质心的定义为
p_c=\frac{1}{m}\int_V \left(p_c+r\right) \rho dV=\frac{1}{m}\int_V p_c \rho dV+\frac{1}{m}\int_Vr \rho dV=p_c+\frac{1}{m}\int_Vr \rho dV

根据叉乘的定义\omega\times r=S\left(\omega\right)\cdot r-r\times\omega=-S\left(r\right)\cdot \omega，因此：

\int_V \left(\omega \times r\right)^T\left(\omega \times r\right)\rho dV=\int_V \left(\omega^TS^T\left(r\right)S\left(r\right)\omega\right)\rho dV=\omega^T\int_V S^T\left(r\right)S\left(r\right)\rho dV \omega

令I=\int_V S^T\left(r\right)S\left(r\right)\rho dV则：

\int_V \left(\omega \times r\right)^T\left(\omega \times r\right)\rho dV=\omega^TI\omega

因此任意刚体动能可以表示为：

E=\frac{1}{2}m\dot{p}_c^T \dot{p}_c\left(质心平移\right) + \frac{1}{2}\omega^T I \omega\left(绕质心的旋转\right)

机器人学中的势能通常指的是重力势能，高中的时候我们学过小滑块的重力势能为U=mgh，这是一种重力势能的标量简化表达式，实际重力势能的矢量定义可以从作功的角度出发（重力作正功，重力势能减小；重力作负功，重力势能增加）因此，质点的重力势能可以表达为U=-mg^Tp（力和位移的点积即为功）。那么对于刚体来说它的重力势能也可以从质量微元的角度出发进行推导：

U=-\int_V g^Tp\ \rho dV=-g^T\int_V p\ \rho dV=-mg^Tp_c

可见刚体重力势能与质点重力势能定义相同。

3.2 二连杆平面臂的动能和势能

  上一节我们定义了任意刚体的动能和重力势能。同样的，刚体的动能和重力势能如果能在质心坐标系下定义将带来同样的好处（牛顿欧拉法中提到的，转动惯量变为常量等）。因此二连杆平面臂的动能和重力势能计算关键依然是求取连杆质心坐标系下的线速度和角速度。由于所有惯性系平权，我们可以把任意刚体的动能和重力势能在刚体质心坐标系下计算（所谓在质心坐标系下计算是指将刚体的速度，角速度，惯量等都在质心坐标系下表达）。同样因为惯性系平权不管我们在哪个坐标系下计算所得连杆的动能和势能都是相等的（我们选择的坐标系都是相对基坐标系静止的）。
动能可以表达为：

E=\frac{1}{2}m\dot{p}_c^T \dot{p}_c + \frac{1}{2}\omega^T I \omega=\frac{1}{2}m\left(R^T\dot{p}_c\right)^T\left(R^T\dot{p}_c\right) + \frac{1}{2}\left(R^T\omega\right)^TI_c\left(R^T\omega\right)=\frac{1}{2}m\left(\dot{p}_c^{i}\right)^T\dot{p}_c^i+\frac{1}{2}\left(\omega^i\right)^T I_c \omega^i

其中I代表的是在基坐标系下表达的（注意这里所说的基坐标系原点是和连杆质心重合的，看一看I与向量r的关系以及向量r在图2中对应的是哪一部分你就清楚了，这一点很重要）连杆惯性张量，I_c代表的是连杆质心坐标系下表达的惯性张量（质心坐标系与连杆坐标系方向相同只是原点位置不同），这也是我们在进行机器人动力学参数辨识时，待辨识的参数。
  从E的表达式可以看出若要求解连杆的动能需要知道连杆质心的线速度、角速度在质心坐标系下的表达。
势能可以表达为：

U=-m\left(R^Tg\right)^T \left(R^Tp_c\right)=-m\left(g^i\right)^T p_c^i

其中R表示的是连杆i的质心坐标系在基坐标系中的姿态表达。
  从U的表达式可以看出若要求解连杆的势能需要知道连杆质心的位置矢量、重力加速度矢量在连杆质心坐标系下的表达。
  总结一下，拉格朗日法中我们可以借助牛顿欧拉法前向递推的思想得到每个连杆的质心速度、连杆角速度等在连杆质心坐标系下的表示，进而计算每个连杆的动能和势能。其实不这样做也可以，只需要求出所有连杆质心速度、连杆角速度在基坐标系下的表达也是可以的。比如势能表达：

U=-m\left(R^Tg\right)^T \left(R^Tp_c\right)=-m\left(g^i\right)^T p_c^i(连杆质心坐标系下形式)=-mg^TRR^Tp_c=\color{red}{-mg^Tp_c(基坐标系下形式)}

形式上（和数值上）两者是完全相同的。
动能的表达：

E=\frac{1}{2}m\dot{p}_c^T \dot{p}_c + \frac{1}{2}\omega^T I \omega=\frac{1}{2}m\left(R^T\dot{p}_c\right)^T\left(R^T\dot{p}_c\right) + \frac{1}{2}\left(R^T\omega\right)^TI_c\left(R^T\omega\right)=\frac{1}{2}m\left(\dot{p}_c^{i}\right)^T\dot{p}_c^i+\frac{1}{2}\left(\omega^i\right)^T I_c \omega^i=\color{red}{\frac{1}{2}m\dot{p}_c^T \dot{p}_c + \frac{1}{2}\omega^T R I_c R^T \omega}

通过推导我们发现尽管基坐标系下表达的惯性张量不是定值，但是他与连杆的质心坐标系下惯性张量参数有着确定的关系：

I=RI_cR^T

因此在基坐标系下计算动能也并不复杂。
  也就是说二连杆平面臂的总能量既可以在各个连杆的质心坐标系下去计算，也可以在基坐标系下去计算。这里我们选择在基坐标系下去计算连杆的总能量。

3.2.1 建立坐标系

  还是用改进（修改）DH法建立连杆坐标系，如下图3所示。

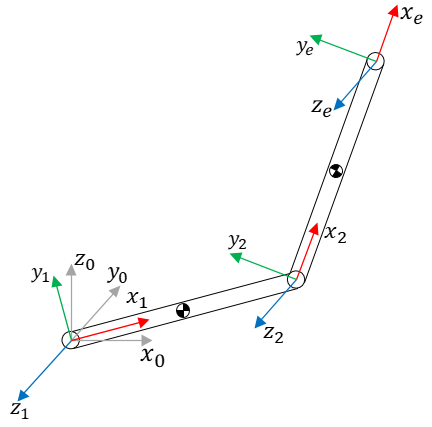
图3 二连杆平面臂建系

符号约定：
x_0y_0z_0：基坐标系
x_1y_1z_1：连杆1坐标系（link 1 frame）
x_2y_2z_2：连杆2坐标系（link 2 frame）
x_ey_ez_e：末端工具坐标系（end effector frame），末端执行器坐标系是固定在连杆2的末端的
l_1：连杆1的长度
l_2：连杆2的长度
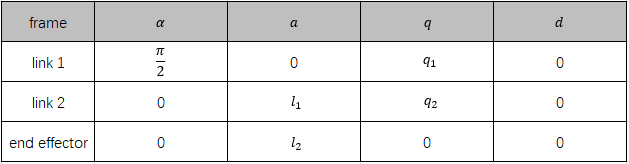
建系完成后对应的改进DH参数表如下表1所示。

表1 二连杆平面臂改进DH参数

T_1=\begin{pmatrix}
R_1& p_1\\
0 &1
\end{pmatrix}基坐标系和连杆1坐标系之间的变换关系

T_2=\begin{pmatrix}
R_2& p_2\\
0 &1
\end{pmatrix}连杆1坐标系和连杆2坐标系之间的变换关系

3.2.2 动能和势能的计算过程

  由易到难先说连杆1质心位置矢量，理解一下3.2.1小节T_1的含义，它描述的就是连杆1坐标系相对于基坐标系的位置及姿态。利用DH变换的公式可以得到：

T_1=rot_x\left(\frac{\pi}{2}\right)\cdot transl_x\left(0\right)\cdot rot_z\left(q_1\right)\cdot transl_z(0)=\begin{pmatrix}
cos(q_1)&-sin(q_1)&0&0\\
0&0&-1&0\\
sin(q_1)&cos(q_1)&0&0\\
0&0&0&1
\end{pmatrix}

从图3中可以看到，在连杆1坐标系下，连杆1质心可以表达为p_{c1}^1=\begin{pmatrix}\frac{l_1}{2}&0&0\end{pmatrix}^T，因此连杆1质心在基坐标系下可以表达为：

p_{c1}=T_1\cdot \begin{pmatrix}p_{c1}^1\\1\end{pmatrix}=\begin{pmatrix}\frac{l_1cos\left(q_1\right)}{2}&0&\frac{l_1sin\left(q_1\right)}{2}&1\end{pmatrix}^T

  基坐标系下重力加速度可以表达为g=\begin{pmatrix}0&0&-9.81\end{pmatrix}^T，连杆1的质量为m_1，因此连杆1的重力势能为：

U_1=-m_1g^Tp_{c1}

  接下来看连杆2质心位置矢量，同样看一下3.2.1小节T_2的含义，它描述的就是连杆2坐标系相对于连杆1坐标系的位置及姿态。利用DH变换公式可以得到：

T_2=rot_x\left(0\right)\cdot transl_x\left(l_1\right)\cdot rot_z\left(q_2\right)\cdot transl_z\left(0\right)=\begin{pmatrix}cos\left(q_2\right)&-sin\left(q_2\right)&0&l_1\\
sin\left(q_2\right)&cos\left(q_2\right)&0&0\\
0&0&1&0\\
0&0&0&1
\end{pmatrix}

从图3中可以看到，在连杆2坐标系下，连杆2质心可以表达为p_{c2}^2=\begin{pmatrix}\frac{l_2}{2}&0&0\end{pmatrix}^T，因此连杆2质心在基坐标系下可以表达为：

p_{c2}=T_1\cdot T_2 \cdot \begin{pmatrix}p_{c2}^2\\1\end{pmatrix}=\begin{pmatrix}\frac{l_2cos\left(q_1+q_2\right) }{2}+ l_1cos\left(q_1\right)\\0\\\frac{l_2sin\left(q_1+q_2\right)}{2}+l_1sin\left(q_1\right)\\1\end{pmatrix}

连杆2的质量为m_2，因此连杆2的重力势能为：

U_2=-m_2g^Tp_{c2}

  以上我们完成了二连杆平面臂重力势能的计算，接下来我们介绍两个连杆动能的计算，这个过程相对于重力势能的计算要复杂一些。根据前面的介绍，刚体的动能在基坐标系下可以表达为：

E=\frac{1}{2}m\dot{p}_c^T \dot{p}_c + \frac{1}{2}\omega^T R I_c R^T \omega

因此想要求得某个连杆的动能，需要得到的物理量有：
1.连杆质心线速度在基坐标系下的表达（\dot{p}_c）
2.连杆角速度在基坐标系下的表达（\omega）
3.连杆质心坐标系相对于基坐标系的旋转矩阵（R）

需要说明的是这里面I_c表达的是质心坐标系下的连杆惯性张量，也正是我们在动力学参数辨识中待辨识的量。由于前面我们已经求出了T_1和T_2，因此两个连杆质心坐标系相对于基坐标系的旋转矩阵R_1和R_2就相应的确定下来了，因此这里不再讨论，我们重点看一下如何求两个连杆角速度和质心线速度。

  在5. 机器人动力学—-串联机构牛顿欧拉方程中我们提到在牛顿欧拉法中有两个递推的过程，前向递推用于求取各个连杆角速度、角加速度、质心线速度；反向递推用于求取各个关节的力和力矩。你会发现前向递推求得的连杆角速度和连杆质心线速度正是我们这里需要的。因此利用前向递推法是求解各连杆角速度和质心线速度的一种思路。
  在13. 机器人正运动学—-雅可比矩阵(1)中我们介绍了雅可比矩阵。回忆一下雅可比矩阵描述的是机器人上某个坐标系（如末端执行器坐标系）的位姿变化率与机器人各个关节的角速度之间的关系。因此对于机器人上的任何一个坐标系都可以找到雅可比矩阵！按照这个思路如果我们能够得到连杆1及连杆质心坐标系处的雅可比矩阵，那么一旦我们知道各个关节的角速度就可以得到对应坐标系在笛卡尔空间下的线速度和角速度。最直观的雅可比矩阵求解方法当然是几何法。相比于前向递推方法，使用这种雅可比的方法要更加直接一些。因此这里我们使用雅可比矩阵的方法来求解各个连杆角速度和质心线速度。
  先来看连杆1质心坐标系对应的雅可比矩阵，从图3中你可以看到关节2的旋转并不会导致连杆1坐标系在空间中运动，因此雅可比矩阵的第二列为全零列。再来看关节1是旋转关节，根据前面文章的介绍连杆1质心坐标系速度和角速度与关节1角速度之间的关系可以表达为：

\begin{pmatrix}v\\\omega\end{pmatrix}=\begin{pmatrix}z_1\times\overrightarrow{O_1O_{c1}}\\z_1\end{pmatrix}\dot{q}_1

z_1是连杆1坐标系的z轴，也就是齐次变换矩阵T_1的第三列z_1=\begin{pmatrix}0 & -1& 0\end{pmatrix}^T。连杆1坐标系原点O_1与基坐标系原点重合，因此O_1=\begin{pmatrix}0&0&0\end{pmatrix}^T，因此\overrightarrow{O_1O_{c1}}实际上就是连杆1质心矢量p_{c_1}。因此连杆1质心坐标系处的雅克比矩阵表达为：

\begin{pmatrix}v_1\\omega_1\end{pmatrix}=\begin{pmatrix}\frac{-l1sin\left(q_1\right)}{2}&0\\
0&0\\
\frac{l1cos\left(q_1\right)}{2}&0\\
0&0\\
-1&0\\
0&0\end{pmatrix}\begin{pmatrix}\dot{q}_1\\dot{q_2}\end{pmatrix}

其中v_1代表的是连杆1质心线速度在基坐标系下的表达，\omega_1代表的是连杆1质心角速度在基坐标系下的表达。
  再来看连杆2，根据前面雅克比矩阵相关文章的介绍我们很容易得到连杆2质心坐标系处的雅克比矩阵表达为：

\begin{pmatrix}v_2\\\omega_2\end{pmatrix}=\begin{pmatrix}z1\times\overrightarrow{O_1O_{c2}}&z_2\times\overrightarrow{O_2O_{c2}}\\
z_1&z_2\end{pmatrix}\begin{pmatrix}\dot{q}_1\\\dot{q}_2\end{pmatrix}

其中z_1=\begin{pmatrix}0 & -1& 0\end{pmatrix}^T，O_1=\begin{pmatrix}0&0&0\end{pmatrix}^T，O_{c2}描述的是连杆2质心坐标系原点也就是p_{c2}，因此\overrightarrow{O_1O_{c2}}实际就是连杆2质心处的位置矢量。O_2代表的是连杆2坐标系原点，也就是T_1\cdot T_2对应的第四列，故：

O_2=\begin{pmatrix}l_1cos\left(q_1\right)&0&l_1sin\left(q_1\right)\end{pmatrix}^T

因此：

\overrightarrow{O_2O_{c2}}=O_{c2}-O_2=\begin{pmatrix}\frac{l_2cos\left(q_1+q_2\right) }{2}+ l_1cos\left(q_1\right)\\0\\\frac{l_2sin\left(q_1+q_2\right)}{2}+l_1sin\left(q_1\right)\end{pmatrix}-\begin{pmatrix}l_1cos\left(q_1\right)\\0\\l_1sin\left(q_1\right)\end{pmatrix}=\begin{pmatrix}\frac{l_2cos\left(q_1+q_2\right) }{2}\\0\\\frac{l_2sin\left(q_1+q_2\right)}{2}\end{pmatrix}

z_2描述的是连杆2坐标系的z轴，也就是齐次变换矩阵T_1\cdot T_2对应的第三列，故z_2=\begin{pmatrix}0&-1&0\end{pmatrix}^T。（其实对于这种二连杆平面臂来说z_1和z_2直接就可以从图3中观察出来，因为他们都和基坐标系的y轴重合，只是方向相反。）。这样所有的变量就都求解出来了，因此连杆2的雅克比矩阵表达为：

\begin{pmatrix}v_2\\omega_2\end{pmatrix}=\begin{pmatrix}\frac{-l_2sin\left(q_1+q_2\right)}{2}-l_1sin\left(q_1\right)&\frac{-l_2sin\left(q_1+q_2\right)}{2}\\
0&0\\
\frac{l_2cos\left(q_1+q_2\right)}{2}+l_1cos\left(q_1\right)&\frac{l_2cos\left(q_1+q_2\right)}{2}\\
0&0\\
-1&-1\\
0&0\end{pmatrix}\begin{pmatrix}\dot{q}_1\\dot{q}_2\end{pmatrix}

3.3 动力学拉格朗日推导

   前面的3.2节我们已经得到了所有用于求解连杆动能和势能的物理量，接下来就可以通过编程来求解二连杆平面臂的动能和势能了。机械臂能量求解完成之后通过matlab提供的diff函数求解牛顿欧拉方程就非常容易了。二连杆平面臂拉格朗日法动力学推导代码如下：

syms l1 l2 m1 m2 g real;
% declare symbolic function of time, so we can compute the derivative of 
% the symbolic function(such as q1(t)) with respect to t.
syms q1(t) q2(t) dq1(t) dq2(t);

syms L_1xx L_1xy L_1xz L_1yy L_1yz L_1zz real;
syms L_2xx L_2xy L_2xz L_2yy L_2yz L_2zz real;
syms l_1x l_1y l_1z l_2x l_2y l_2z real;
l_1x = l1/2;
l_1y = 0;
l_1z = 0;
l_2x = l2/2;
l_2y = 0;
l_2z = 0;
% declare that the symbolic function is a real(not imaginary) function 
% see also:
% https://www.mathworks.com/matlabcentral/answers/457466-issue-with-reality-assumption-of-an-implicit-function
% https://www.mathworks.com/matlabcentral/answers/78614-how-do-you-declare-a-symbolic-function-of-time-as-a-real-variable
assumeAlso(q1(t), 'real');
assumeAlso(q2(t), 'real');
assumeAlso(dq1(t), 'real');
assumeAlso(dq2(t), 'real');

G = [0; 0; g];
% formula is a function to get the body of the symbolic function using
% which you can do slicing operation just like the matrix(such as T1(1:3, 1:3))
% see also:
% https://www.mathworks.com/help/symbolic/sym.formula.html
% https://www.mathworks.com/matlabcentral/answers/260444-use-a-symfun-as-index-of-a-matrix
T1 = formula([cos(q1) -sin(q1) 0 0; 0 0 -1 0; sin(q1) cos(q1) 0 0;0 0 0 1]);
T2 = formula([cos(q2) -sin(q2) 0 l1; sin(q2) cos(q2) 0 0; 0 0 1 0; 0 0 0 1]);
T20 = T1*T2;
pc1 = formula(simplify(T1 * [l_1x; 0; 0; 1]));
pc1 = pc1(1:3);
pc2 = formula(simplify(T1 * T2 * [l_2x; 0; 0; 1]));
pc2 = pc2(1:3);
U1 = -m1 * G' * pc1;
U2 = -m2 * G' * pc2;

z1 = T1(1:3,3);
o1 = [0; 0; 0];
oc1 = pc1;
o1oc1 = pc1 - o1;
J1c = [cross(z1, o1oc1) zeros(3,1); z1 zeros(3,1)];
vw1 = formula(J1c * [dq1; dq2]);
v1 = formula(vw1(1:3));
w1 = formula(vw1(4:6));
R1 = T1(1:3, 1:3);
I1 = [L_1xx L_1xy L_1xz; L_1xy L_1yy L_1yz; L_1xz L_1yz L_1zz];
E1 = 1/2 * m1 * v1' * v1 + 1/2 * w1' * R1 * I1 * R1' * w1;

o2 = T20(:,4);
o2 = o2(1:3);
oc2 = pc2;
o1oc2 = oc2 - o1;
o2oc2 = oc2 - o2;
z2 = T20(1:3, 3);
J2c = [cross(z1, o1oc2) cross(z2, o2oc2); z1 z2];
vw2 = formula(J2c * [dq1; dq2]);
v2 = vw2(1:3);
w2 = vw2(4:6);
R2 = T20(1:3, 1:3);
I2 = [L_2xx L_2xy L_2xz; L_2xy L_2yy L_2yz; L_2xz L_2yz L_2zz];
E2 = 1/2 * m2 * v2' * v2 + 1/2 * w2' * R2 * I2 * R2' * w2;

L = simplify(E1 + E2 - U1 - U2);

% lagrange equation
tau1 = formula(diff(diff(L, dq1), t) - diff(L, q1));
tau2 = formula(diff(diff(L, dq2), t) - diff(L, q2));

syms q1(t) q2(t) dq1(t) dq2(t);
assumeAlso(q1(t), 'real');
assumeAlso(q2(t), 'real');
assumeAlso(dq1(t), 'real');
assumeAlso(dq2(t), 'real');
syms ddq1 ddq2;
tau1 = subs(tau1, diff(dq1(t), t), ddq1);
tau1 = subs(tau1, diff(dq2(t), t), ddq2);
tau1 = subs(tau1, diff(q1(t), t), dq1);
tau1 = subs(tau1, diff(q2(t), t), dq2);
tau1 = simplify(tau1);


tau2 = subs(tau2, diff(dq1(t), t), ddq1);
tau2 = subs(tau2, diff(dq2(t), t), ddq2);
tau2 = subs(tau2, diff(q1(t), t), dq1);
tau2 = subs(tau2, diff(q2(t), t), dq2);
tau2 = simplify(tau2);

  整个代码实现还是非常简单的，很多地方与3.2节的公式是一一对应的，这里简单提一下matlab里面比较实用的几个技巧：
1.符号推导时可以通过定义syms q(t)这样的方式定义一个可以对时间t求导的符号函数
2.assumeAlso告知matlab对应的符号函数具备怎样的特性，这里用它说明符号函数是实函数
3.formula用于提取符号函数的定义，否在我们在使用切片操作（如T1(1:3, 1:3)）会发生错误
4.subs用于求值，将符号表达式的匹配项修改为其他自定义项，用于进行符号表达的简化
你可以仿照7. 机器人动力学—-二连杆平面臂动力学仿真验证验证这里推导的结果或者可以与6. 机器人动力学—-二连杆平面臂牛顿欧拉推导牛顿欧拉法的结果进行对比会发现两个计算结果是完全一致的。

4. 总结

  这篇文章主要介绍了二连杆平面臂动力学推导的拉格朗日法。后续文章暂时岔开动力学部分，介绍一下机械臂的逆解问题。之后我们再回到动力学这个话题介绍更加通用的动力学推导方法，动力学参数辨识等内容。
  由于个人能力有限，所述内容难免存在疏漏，欢迎指出，欢迎讨论。

5. 参考文献

[1]. 机器人学 建模、规划与控制 西西里安诺