———— 陟彼高岗，我马玄黄；我姑酌彼兕觥，维以不永伤。

稀疏核机 (Sparse Kernel Machine)

前⼀章中讨论的核方法在训练阶段需要对所有训练点进行两两计算核函数，由于时间复杂度过高在数据集较大时几乎是不可⾏的，并且在预测时也会花费过多的时间。本章我们会讨论具有稀疏 (sparse) 解的核算法，一种对新数据的预测只依赖于训练数据的⼀个⼦集上计算的核函数，这通常被称为稀疏核机 (sparse kernel machine)。本章重点讨论⽀持向量机 (support vector machine, SVM)，这就是一种稀疏核机，下面会通过一个例子解释它的名称以及稀疏性来源。这是一种很流行的算法，常常被用来解决分类和回归问题。⽀持向量机的⼀个重要性质是模型参数的确定对应于⼀个凸优化问题，因此许多局部解也是全局最优解。

支持向量机 (Support Vector Machine)

我们首先通过一个二分类问题引出支持向量机，然后再讨论其与核函数的关系。假设线性基函数模型为

训练数据集  由  个输入向量  组成，对应目标值为  ，其中  。假设训练数据集在特征空间中是线性可分的，即对于所有的训练数据都有  。这与感知器一节中的定义相同，在感知器算法中，我们通过在有限步骤内不断迭代寻找出一个解，但是这种解实际上可能有多个，感知器算法最终寻找到哪个解依赖于参数的初始化，对于可能存在的多个解，我们应该寻找泛化误差最小的那个，在支持向量机中，就引入了边缘 (margin) 的概念，即决策边界与任意样本之间的最⼩距离，如下图所示

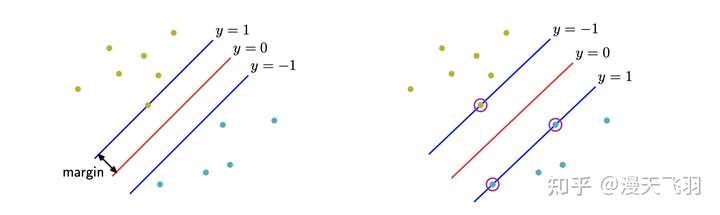
在⽀持向量机中，决策边界被选为使边缘最⼤化的那个边界。已有相关高斯核方法证明了最优超平⾯是有着最⼤边缘的超平⾯，距离超平⾯较近的点对超平⾯的影响⼤于距离较远的点，在高斯核参数取极限的情况下，超平⾯会变得与那些距离较远的点无关，也就是在核方法不再考虑这些点，这就是支持向量机稀疏性的来源，对于那些有决定意义的点，我们就称之为支持向量，因此这种方法就叫做支持向量机。

在第三章线性分类中，我们提过点  距离由  定义的超平⾯的垂直距离为  ，我们需要考虑的是那些能够被正确分类的数据点，即  ，因此点  距离决策⾯的距离为

边缘由数据集⾥垂直距离最近的点  给出，我们希望最优化参数  和  ，使得这个距离最大化，通过下式得到

优化上式的关键是找出最近的点  ，这就需要对  进行一些限制同时不影响到决策面的距离，由于对参数  和  进行同比例缩放并不会改变任意点  到决策面的距离  ，可以利用这个性质，假设有一组参数恰好使距离决策面最近的点  有

这时所有的点都会满足

根据公式 (5) 定义及上图不难看出，当找到这个最大化的边缘后，至少存在两个  使公式 (5) 取等号。这样最优化问题就简化为最⼤化  ，这里做一些小小的变换，将问题转换为最⼩化  ，这是为了变成一个二次规划 (quadratic programming) 问题，即在⼀组线性不等式的限制条件下最⼩化⼆次函数，之所以这样做是因为二次型是一个凸函数且易于优化分析。因此我们要在限制条件 (4) 下，求解最优化问题

为了解决这个限制的最优化问题，我们引⼊拉格朗⽇乘数  。由于并不知道最近的点是哪个，我们考虑所有数据，令公式 (5) 中的每个限制条件都对应⼀个乘数  ，从⽽可得下⾯的拉格朗⽇函数

其中  ，对于公式 (7)，我们要做关于  和  的最小化，关于  的最大化。首先令  关于  和  的导数为零，可得

公式 (8) 恰好就是上一章对偶表示中参数的表示方法，使⽤这两个条件从  中消去  和  ，就得到了最⼤化边缘问题的对偶表示，于是再转换为关于  的最大化

其中  。公式 (10) 右侧第二项让核函数  正定这⼀限制条件存在的原因变得很显然，因为必须确保拉格朗⽇函数  有上界，从⽽使最优化问题有良好的定义。关于公式 (10) 的求解在后文会提及，我们直接看对新输入数据  的预测，将公式 (8) 替换公式 (1) 中的参数项，可得

第六章学习理论一节有介绍拉格朗日乘数法，拉格朗日乘数法的最优化函数成立需要满足 Karush-Kuhn-Tucker 条件，即假设拉格朗日函数形式为

要利用这个函数最大化  ，需要同时满足  ，对于公式 (7)，我们还需要满足

任何使得  的数据点都不会出现在公式 (11) 的求和式中，因此对新数据点的预测没⽤，剩下的数据点才能被称为⽀持向量 (support vector)。由于这些⽀持向量满⾜  ，因此它们对应于特征空间中位于最⼤边缘超平⾯上的点。这个性质是⽀持向量机在实际应⽤中的核⼼，⼀旦模型被训练完毕，相当多的数据点都可以被丢弃，只有⽀持向量被保留。

在解决二次规划并找到  之后，根据  ，代入公式 (11)，即可确定参数  的值

其中  是  中支持向量的下标集合，虽然我们能⽤任意⽀持向量  解这个关于  的⽅程，但通过下⾯的⽅式可以得到⼀个在数值计算上更加稳定的解。⾸先乘以  ，使⽤  的性质，然后对所有⽀持向量整理⽅程，解出  ，可得

其中  是⽀持向量的总数。

接下来我们可以将最⼤边缘分类器⽤带有简单⼆次正则化项的最⼩化误差函数表示，形式为

其中  是一个函数，当  时，函数值为零，其他情况下函数值为  。这就确保了限制条件 (5) 成⽴，只要正则化参数满⾜  ，那么它的精确值就没有作⽤，这样就将模型参数优化为了最⼤化边缘。

1. 重叠类分布

上述讨论中我们假设训练数据点在特征空间  中是线性可分的，解得的⽀持向量机在原 始输⼊空间  中会对训练数据进⾏精确划分，虽然对应的决策边界是⾮线性的。然⽽实际中类条件分布可能重叠，这种情况下对训练数据的精确划分会导致较差的泛化能⼒。

这时我们可以通过修改公式 (16) 误差函数，使得数据点允许在决策边界的错误分类的一侧，但需要增加⼀个惩罚项，这个惩罚项随着与决策边界的距离的增⼤⽽增⼤，令这个惩罚项是距离的线性函数⽐较⽅便。为了完成这⼀点，我们引⼊松弛变量 (slack variable)  ，其中  ，每个训练数据点都有⼀个松弛变量。对于位于正确的边缘边界内部的点或者边界上的点有  ，对于其他点有  ，而对于决策边界  上的点有  ，  就是错误分类的点，这样公式 (5) 的限制条件就变为

 的数据点是位于边缘或边缘正确一侧的正确分类的点，  的点是位于边缘内部，但是在决策边界正确⼀侧的点，  的点是位于决策边界的错误⼀侧的点。这就允许⼀些训练数据点被错误分类。虽然松弛变量允许类分布的重叠，但这个框架对于异常点很敏感，因此误分类的惩罚随着  线性增加。

现在⽬标是最⼤化边缘，同时以⼀种⽐较柔和的⽅式惩罚位于边界错误⼀侧的点。于是，改为最⼩化

其中参数  类似于一个正则化系数，控制两个惩罚项的折中关系。在极限  情况下就是线性可分的支持向量机，现在在公式 (17) 以及  的条件下最⼩化公式 (18)。对应拉格朗⽇函数为

其中  和  是拉格朗日乘数，公式 (19) 对应的 (12) 中的 KKL 条件分别为  ，现在对  进⾏优化，使公式 (19) 对其导数为 0

代入公式 (19) 消除  可得拉格朗日函数

这与公式 (10) 形式上完全相同，唯⼀的区别就是限制条件有些差异。由于拉格朗日乘数  及  ，根据公式 (22) 可知关于对偶变量  最大化公式 (23) 需要满足的限制为  ，  ，这同样又是一个二次规划问题，对新数据的预测同样为公式 (11)，同样我们不关心那些使  的训练数据点，所有支持向量都应该满足

再考虑这些数据点中，如果  ，那么根据限制条件 (22) 有  ，再根据拉格朗日函数 (19) 的 KKL 条件，可得  ，表明这些点位于边缘上，而对于  的点，可根据  是否大于 1 判断是否在错误分类的一边。

为了确定参数  ，因为  的支持向量满足  即  ，所以也可以推导出公式 (14) 和 (15) 的表达式，唯一不同的是，  的解的形式为

其中  表示  的集合，这是因为确定参数  时我们只考虑了  的点，这些事位于边缘上的点，而利用  得出公式 (14) 这样的表达式时我们考虑的是  这些点。

2. 回归问题的 SVM

现在将支持向量机推广到回归模型，假设一个简单的线性回归模型，我们最小化误差函数

为了保持支持向量机的稀疏性，⼆次误差函数会被替换为⼀个  不敏感误差函数，如果预测  和⽬标  的差绝对值⼩于  ，那么这个误差函数给出的误差等于零，其中  。  不敏感误差函数的⼀个简单例⼦是

在不敏感区域之外，会有⼀个与误差相关联的线性代价，如下图所示，绿色代表原平方和误差函数，红色代表支持向量机的  不敏感误差函数

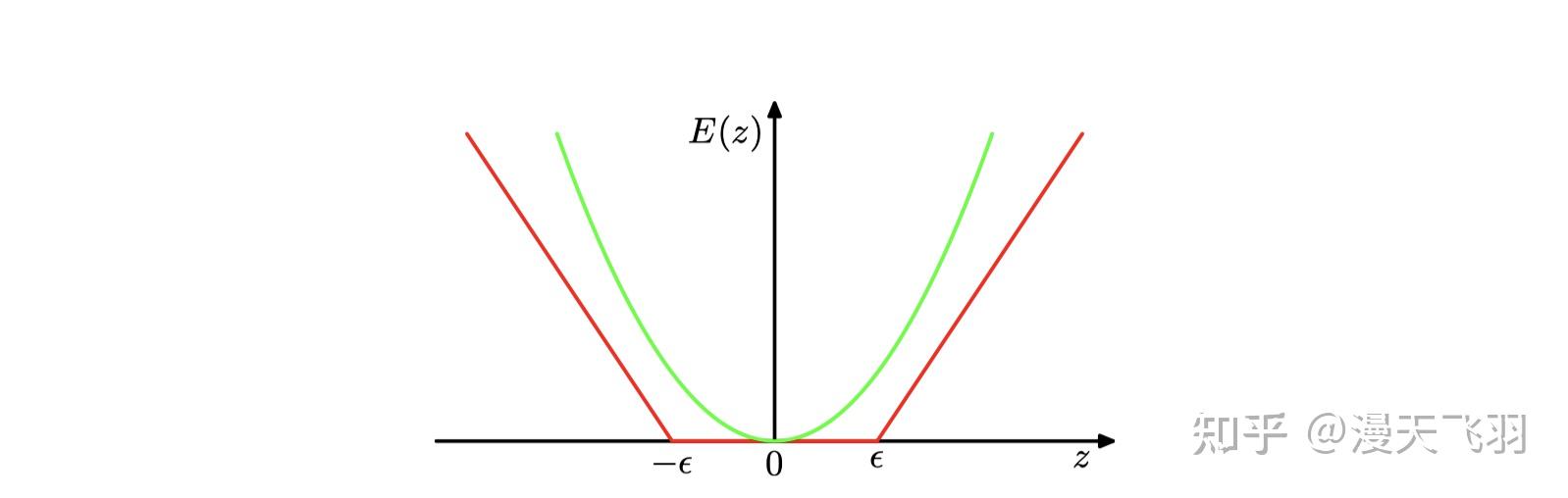
最小化正则化的  不敏感误差函数，同样引入一个正则化系数  ，形式为

与之前一样，我们引入松弛变量最优化表达式，但不同的是，我们需要引入两个松弛变量  ，其中  对应于  的数据点，而  对应于  的数据点，如下图所示

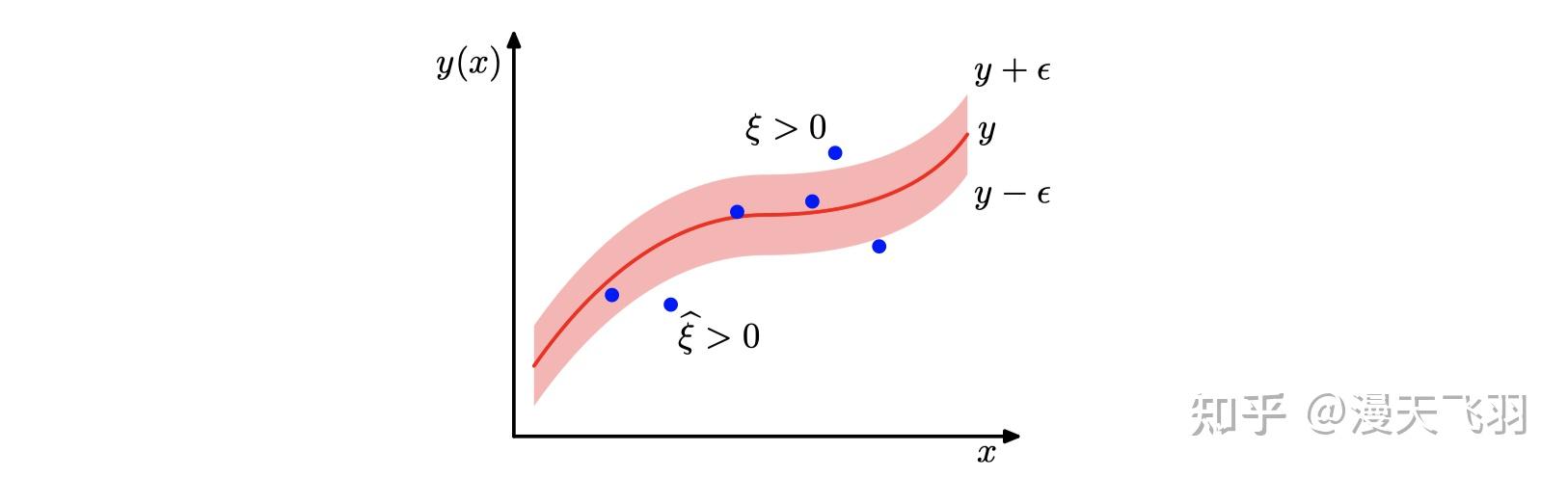
⽬标点位于  管道内的条件是  。引⼊松弛变量使得数据点能够位于管道之外，只要松弛变量不为零即可，对应的条件变为

于是线性回归的支持向量机误差函数变为

对公式 (30) 做限制条件 (29) 以及  下的拉格朗日函数，引入拉格朗日乘数  ，然后最优化

同样使用公式 (1) （此时将公式 (1) 看做线性回归模型）替换  ，然后令拉格朗⽇函数关于  的导数为零，有

使⽤这些结果代换拉格朗⽇函数中对应的变量，可以转换为对偶问题到关于  最⼤化

同样根据公式 (34) 和 (35)，我们可以得出限制条件  ，然后将公式 (32) 代入公式 (1)，对于新的预测变量，就变成了

再次根据拉格朗日函数 (31) 的 KKT 条件，让系数与限制的乘积为零，有

逐一分析，首先看公式 (38)，当  时，数据点要么位于  管道的上边界上  ，要么位于上边界的下⽅  ，类似地，公式 (39) 也可以这样推导，得出数据点位于下边界上或下边界上方的结论。此外两个限制  和  不兼容，通过将两式相加，由于  非负，所以  至少一个为零或都为零。

同样地，支持向量应该是那些对预测有贡献，在参数中可以出现的点，这些点需要满足  或  ，位于  管道边界上或管道外部，我们再次得到了⼀个稀疏解。

关于参数  ，考虑⼀个数据点，满⾜  。根据公式 (40) (38)，⼀定有  ，  ，使⽤公式 (1) 求解  ，有

可以看出，支持向量机的线性回归和线性分类解法思路相差不大，通过对这个过程的推导，我们都可以证明支持向量机的稀疏性，支持向量机也得以广泛应用。