常用的姿态表示方法有欧拉角、方向余弦矩阵、四元数这几种

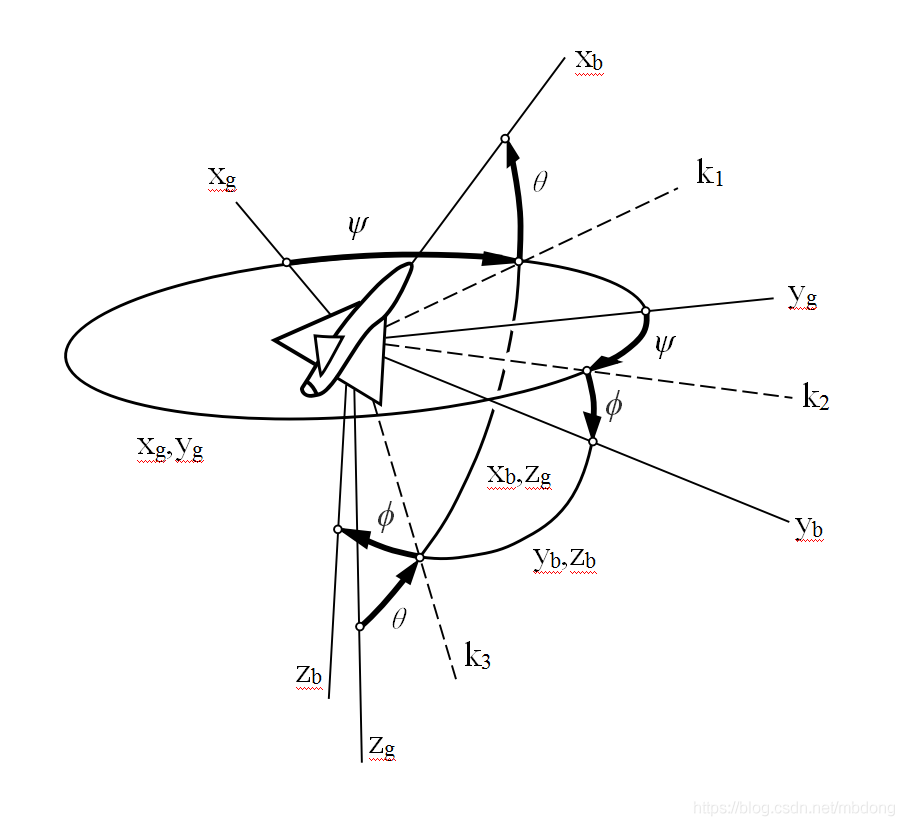
欧拉角表示方法采用(\phi,\theta,\psi)来表示飞行器的姿态，其中\phi为滚转角，\theta为俯仰角和\psi为航向角，表示飞行器首先航向偏转角度，再俯仰角度\psi，然后机体滚转角度\theta得到的姿态

方向余弦矩阵通过机体坐标和地面坐标的转换矩阵（DCM, Directional Cosine Matrix）来表示机体的姿态

四元数通过四个元数(q_0,q_1,q_2,q_3)来表示飞行器全方位的姿态，它的特点是表征方式简洁，并且没有奇异点

欧拉角->方向余弦矩阵

C_{b}^{g}=\begin{bmatrix} \mathrm{cos}\theta\mathrm{cos}\psi & \mathrm{sin}\phi\mathrm{sin}\theta\mathrm{cos}\psi-\mathrm{cos}\phi\mathrm{sin}\psi & \mathrm{cos}\phi\mathrm{sin}\theta\mathrm{cos}\psi+\mathrm{sin}\phi\mathrm{sin}\psi\\ \mathrm{cos}\theta\mathrm{sin}\psi & \mathrm{sin}\phi\mathrm{sin}\theta\mathrm{sin}\psi+\mathrm{cos}\phi\mathrm{cos}\psi &\mathrm{cos}\phi\mathrm{sin}\theta\mathrm{sin}\psi-\mathrm{sin}\phi\mathrm{cos}\psi\\ -\mathrm{sin}\theta & \mathrm{sin}\phi\mathrm{cos}\theta & \mathrm{cos}\phi\mathrm{cos}\theta \end{bmatrix}

其中，C_{b}^{g}表示从机体坐标转换到地面坐标的变换矩阵，C_{g}^{b}为地面坐标到机体坐标的转换矩阵，为C_{b}^{g}的转置

    C_{g}^{b}=(C_{b}^{g})^{T}

欧拉角->四元数

    \\ q_0=\pm \left ( \mathrm{cos}\frac{\phi}{2} \mathrm{cos}\frac{\theta}{2} \mathrm{cos}\frac{\psi}{2}+\mathrm{sin}\frac{\phi}{2} \mathrm{sin}\frac{\theta}{2} \mathrm{sin}\frac{\psi}{2} \right ) \\ q_1=\pm \left ( \mathrm{sin}\frac{\phi}{2} \mathrm{cos}\frac{\theta}{2} \mathrm{cos}\frac{\psi}{2}-\mathrm{cos}\frac{\phi}{2} \mathrm{sin}\frac{\theta}{2} \mathrm{sin}\frac{\psi}{2} \right )\\ q_2=\pm \left ( \mathrm{cos}\frac{\phi}{2} \mathrm{sin}\frac{\theta}{2} \mathrm{cos}\frac{\psi}{2}+\mathrm{sin}\frac{\phi}{2} \mathrm{cos}\frac{\theta}{2} \mathrm{sin}\frac{\psi}{2} \right )\\ q_3=\pm \left ( \mathrm{cos}\frac{\phi}{2} \mathrm{cos}\frac{\theta}{2} \mathrm{sin}\frac{\psi}{2}-\mathrm{sin}\frac{\phi}{2} \mathrm{sin}\frac{\theta}{2} \mathrm{cos}\frac{\psi}{2} \right )

方向余弦矩阵->欧拉角

通过前面的欧拉角到方向余弦矩阵的变换公式，可以逆变换得到从发现余弦矩阵到欧拉角的变换，方便起见记C=C_b^g，则

    \\\phi=\mathrm{atan}(C_{32}/C_{33}) \\\theta=-\mathrm{asin}(C_{31}) \\\psi=\mathrm{atan}(C_{21}/C_{11})

其中，C_{ij}表示方向余弦矩阵的第i行第j列元素

四元数->方向余弦矩阵

    C_{b}^{g}=\begin{bmatrix} q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) &2(q_1q_3+q_0q_2)\\ 2(q_1q_2+q_0q_3) & q_0^2-q_1^2+q_2^2-q_3^2&2(q_2q_3-q_0q_1)\\2(q_1q_3-q_0q_2) &2(q_2q_3+q_0q_1) &q_0^2-q_1^2-q_2^2+q_3^2 \end{bmatrix}

方向余弦矩阵->四元数

根据四元数定义

    q_0^2+q_1^2+q_2^2+q_3^2=1

由四元数和方向余弦矩阵转换矩阵可得

    \\4q_0^2=1+C_{11}+C_{22}+C_{33}\\4q_1^2=1+C_{11}-C_{22}-C_{33}\\ 4q_2^2=1-C_{11}+C_{22}-C_{33}\\ 4q_3^2=1-C_{11}-C_{22}+C_{33}\\

有

    \\q_0=\pm\frac{1}{2}\sqrt{1+C_{11}+C_{22}+C_{33}} \\q_1=\pm\frac{1}{2}\sqrt{1+C_{11}-C_{22}-C_{33}} \\q_2=\pm\frac{1}{2}\sqrt{1-C_{11}+C_{22}-C_{33}} \\q_3=\pm\frac{1}{2}\sqrt{1-C_{11}-C_{22}+C_{33}}

四元数->欧拉角

    利用上面的方向余弦矩阵与欧拉角和四元数的转换关系得到

\\\phi=\mathrm{atan2}(2(q_2q_3+q_0q_1),q_0^2-q_1^2-q_2^2+q_3^2) \\\theta=-\mathrm{asin}(2(q_1q_3-q_0q_2)) \\\psi=\mathrm{atan2}(2(q_1q_2+q_0q_3),q_0^2+q_1^2-q_2^2-q_3^2)

    

    其中

欧拉角、四元数、方向余弦矩阵、姿态表示方法的特点

姿态表示方法里面，欧拉角是比较直观的方法，用三个角度来衡量机体坐标和地面坐标之间的姿态倾转，在小角度时，基本上姿态角就等于倾角，但是它的缺点是非线性特点，在俯仰角接近90度的时候，欧拉角变量会呈现较大的非线性，在90度具有奇异点，不利于计算，它的特点是意义直观，所以欧拉角通常用于向用户表示姿态，而在内部计算和程序实现中，则通常采用四元数或方向余弦矩阵方法。

四元数和方向余弦矩阵的表示方法，都没有奇异点的问题，能够性能一致的表示360度全方位的姿态，在计算过程中，直接对四元数或者方向余弦矩阵数值进行迭代，相比之下四元数的表示更加简洁，计算量更小，而方向余弦矩阵则多一些冗余度和计算值，但是在无人机涉及的坐标转换计算方面更加便利直接，两者都有应用。

参考

https://wenku.baidu.com/view/60696a60647d27284a735129.html