本文主要基于以下参考:
[1] John T. Betts. Survey of Numerical Methods for Trajectory Optimization.
[2] Anil V. Rao. A Survey of Numerical Methods For Optimal Control.
[3] John T. Betts. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming 2nd.
[4] A E. Bryson. Applied Optimal Control.
[5] KIRK. Optimal Control Theory: An Introduction.
[6] Matthew Kelly. An Introduction to Trajectory Optimization: How to Do Your Own Direct Collocation.
第一部分介绍变分法原理:
在 [4] 2.3节中,介绍了连续系统,无终端约束,固定终端时间下的变分法原理。
考虑非线性微分方程:
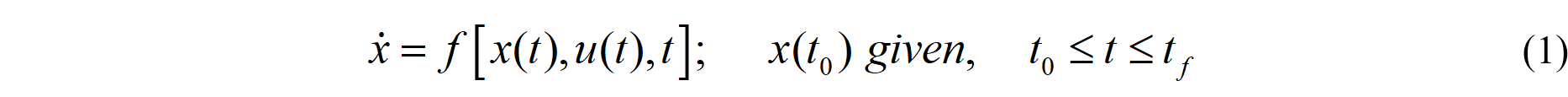
其中, x(t) 为状态, u(t) 为控制,考虑优化指标如下:
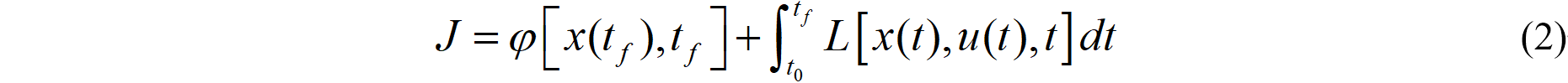
最优控制即是寻找最优控制曲线u(t)来使得优化指标最小。这部分内容与书上完全相同,为了完整性重新抄录在这里。
考虑引入乘子函数 λ(t) ,通过该函数将系统微分方程引入到优化指标中,得到如下:
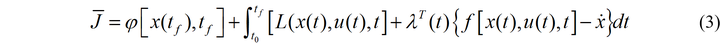
定义标量函数 H 为:

此时,公式(3)变为:
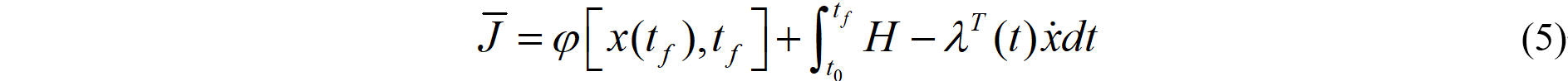
对上式最后一项作分部积分,可以得到:
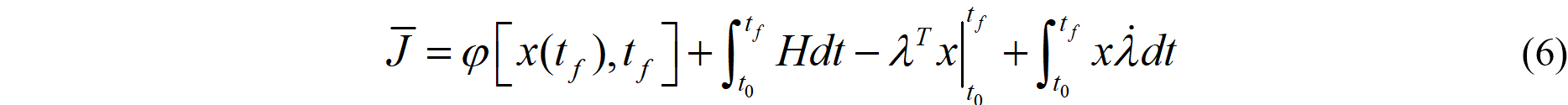
考虑由于控制变量的变分在固定初末时间条件下导致的优化指标函数的变分如下:
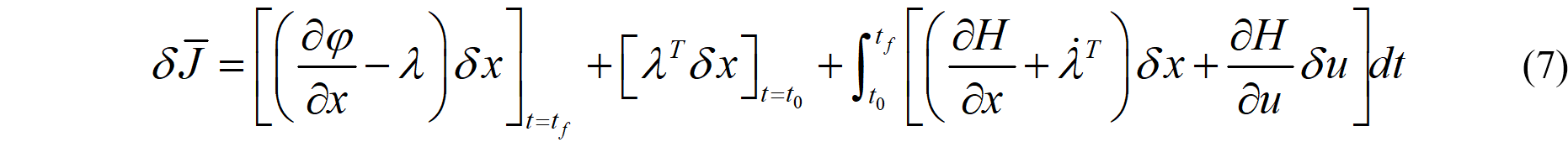
上式中,由于状态变量与控制变量满足系统微分方程,因此控制变量的变化会导致状态的变化。由于上述原因,控制变量的变分与状态变分之间满足某些关系,确定这种关系比较复杂。

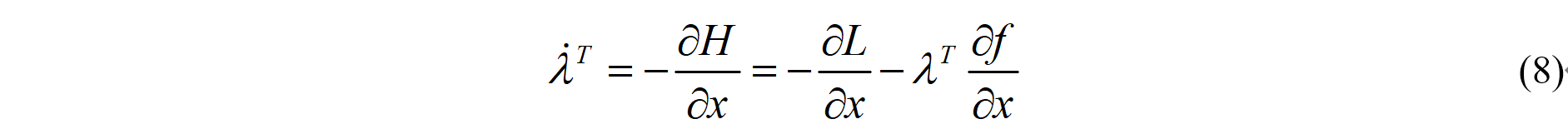
以及边界关系:
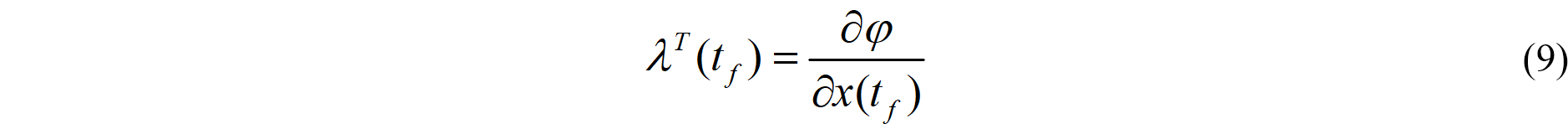
此时,公式(7)变为:
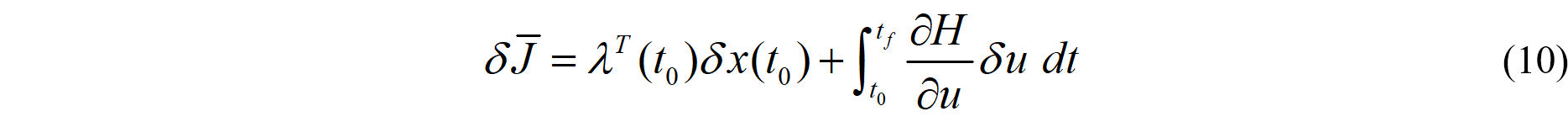
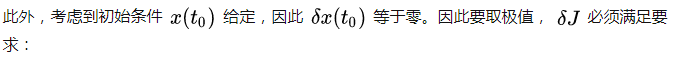
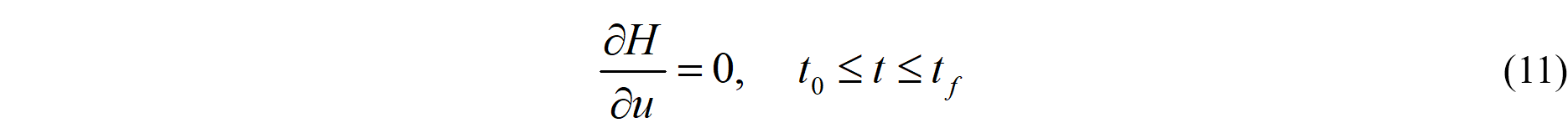
其中,关系式(8)(9)(11)称为变分法中的欧拉—拉格朗日方程。
最优控制问题:
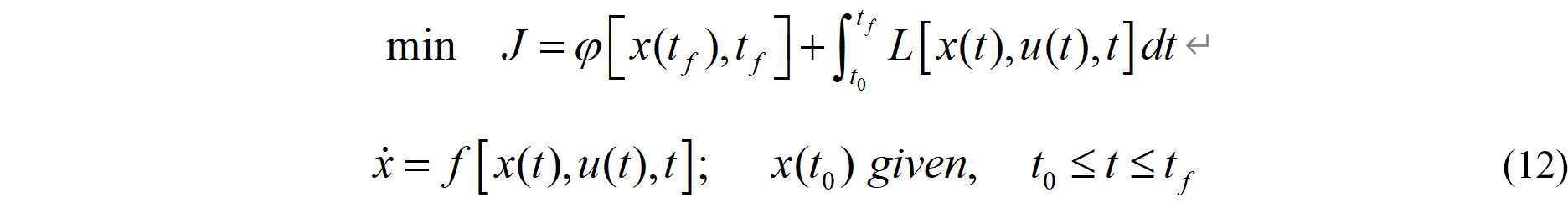
总结,最优控制的最优条件如下:

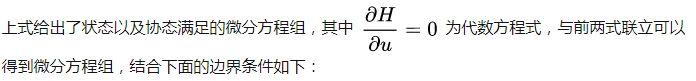
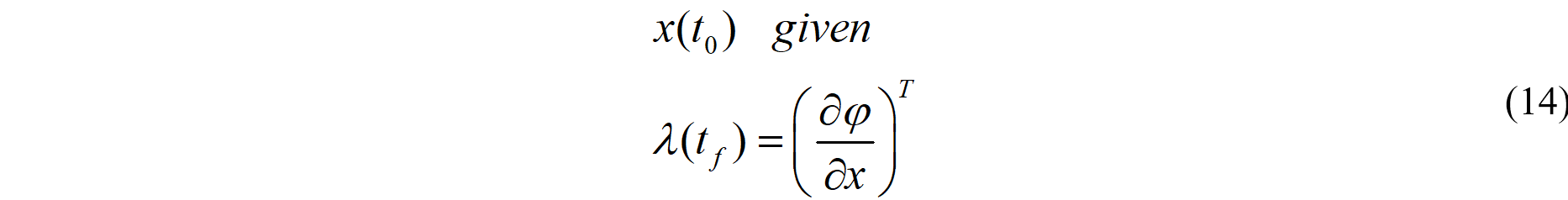
因此,我们得到了最简单最优控制问题的必要性条件,即两点边值问题。
书中还提到了当 L 和 f 不显式依赖于时间 t 时,边值问题的一次积分可以求得:
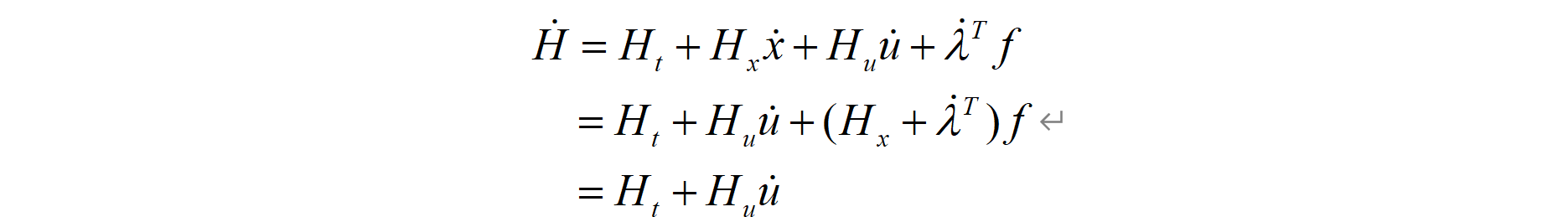
那么,如果当 L 和 f 不显式依赖于时间 t 时,结合前面必要条件,可以得到:
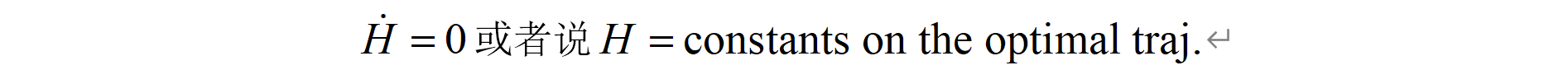
下面举一个简单的最优控制的例子:

最优控制问题:
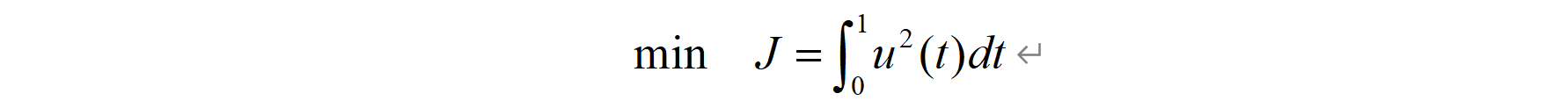
系统动力学为:
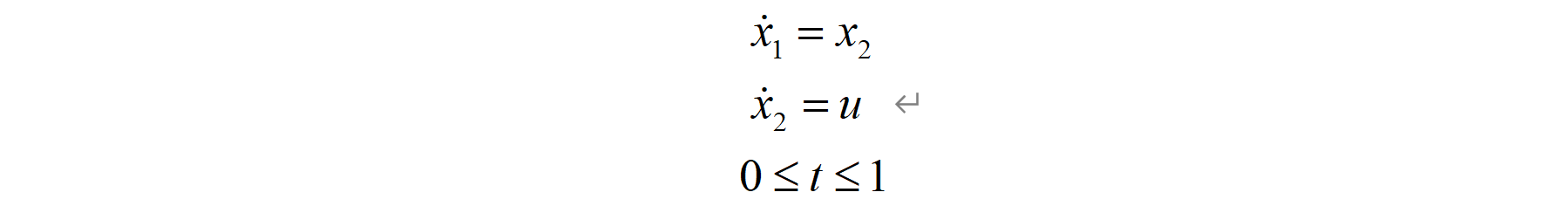
初始终端条件:
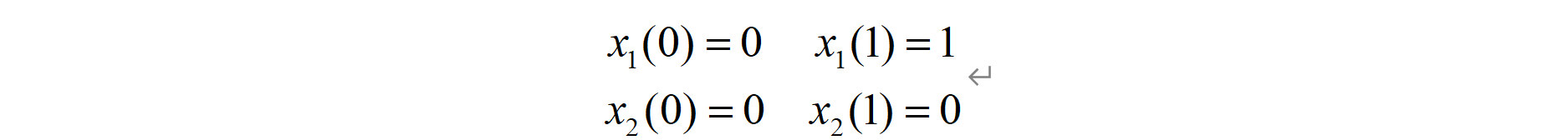
按照上述必要条件对该最优控制问题写出必要条件如下:

联立以后式子可以得到状态和协态的微分方程如下:
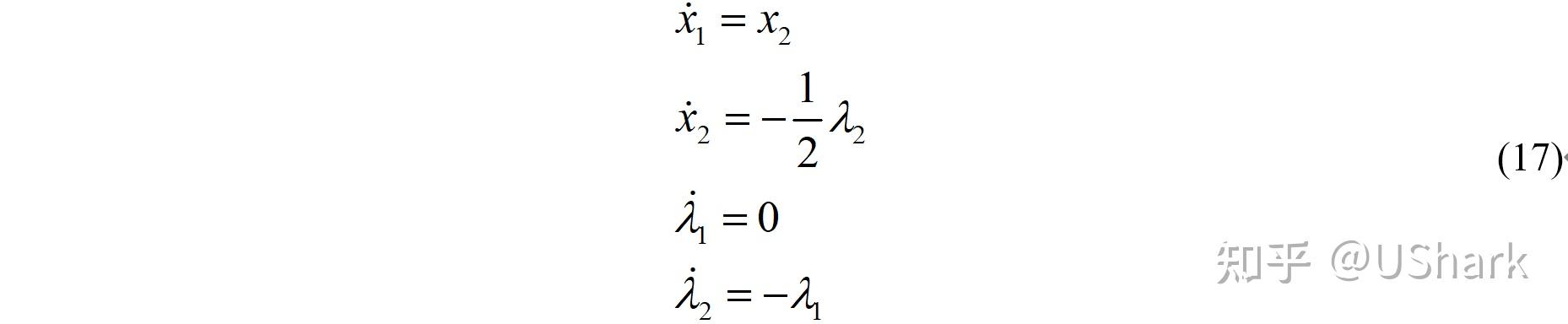
边界条件如下:
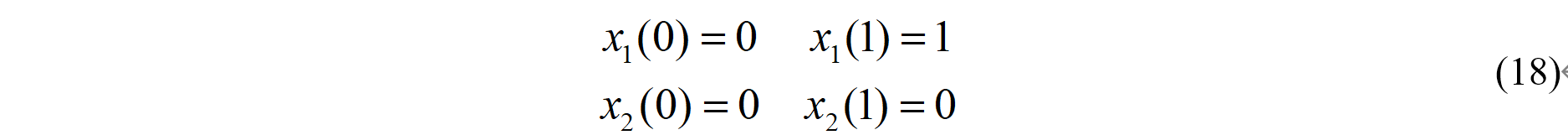
该最优控制解析解如下:
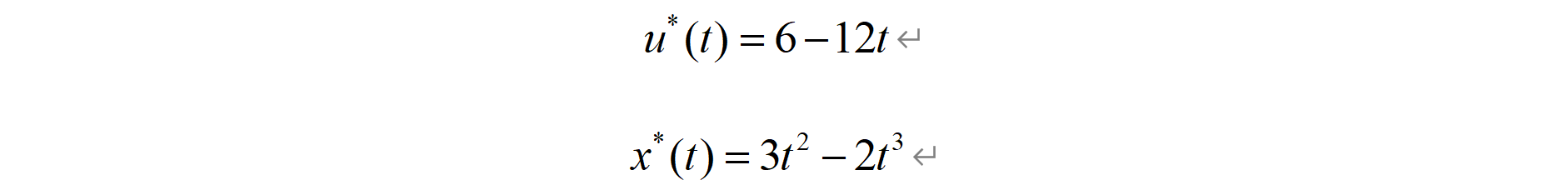
下面首先采用Matlab自带的函数bvp4c来对两点边值问题进行求解:
% given the initial guess
solinit = bvpinit(linspace(0,1,10),[1 0 0 0]);
% solve the problem
sol = bvp4c(@sysdyn,@sysbc,solinit);
% eval points
t = linspace(0, 1, 50);
% eval
y = deval(sol,t);
% plot states
figure(1);
plot(t, y(1,:), 'o-', t, y(2,:),'o-');
grid;
xlabel('time/s');
legend('state 1', 'state 2');
% plot costates
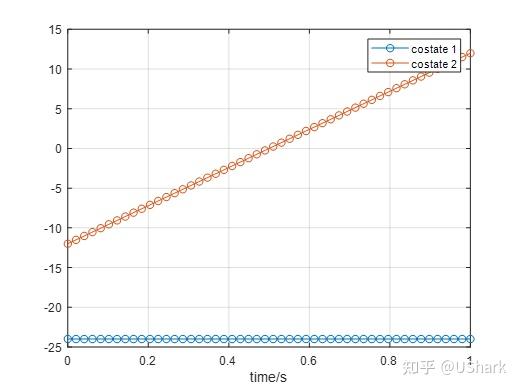
figure(2);
plot(t, y(3,:), 'o-',t, y(4,:),'o-');
grid;
xlabel('time/s');
legend('costate 1', 'costate 2');
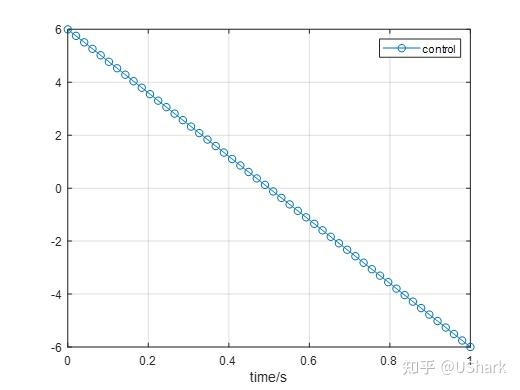
% plot control
figure(3);
plot(t, -0.5*y(4,:),'o-');
grid;
xlabel('time/s');
legend('control');
% 状态依次: x1,x2,lambda1,lambda2
function dydx = sysdyn(t,y)
dydx = [ y(2); -0.5*y(4); 0; -y(3)];
end
function res = sysbc(y0,y1)
res = [ y0(1);y0(2);y1(1)-1; y1(2) ];
end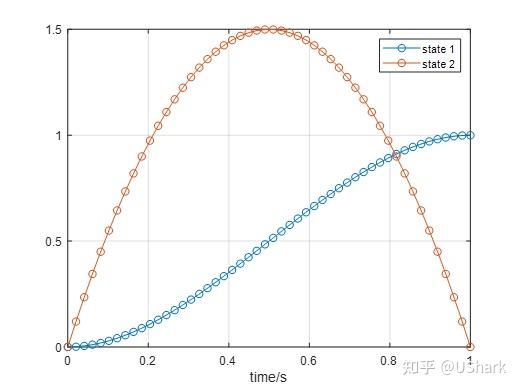






评论(0)
您还未登录,请登录后发表或查看评论