连续LQR理论

LQR (linear quadratic regulator)即线性二次型调节器，是现代控制理论中发展最早也最为成熟的一种状态空间设计法。特别可贵的是，LQR可得到状态线性反馈的最优控制规律，易于构成闭环最优控制。
我们不必现在深度研究最优控制的求极值技巧(极大值原理，古典变分法与动态规划)。除去求最优控制的技巧，优化控制技术的逻辑很简单：给一个系统，给一个性能函数(performance index, 也叫cost function)，求出一个控制序列，使得系统稳定并且性能函数取到极值。至于是取极小值还是极大值，这个取决于求解的问题和性能函数的定义。
LQR的实质与状态反馈没有什么差别，只不过通过了优化性能函数得到一组最优增益矩阵，实现零极点配置（Pole-Placement）。以下是LQR实现的步骤：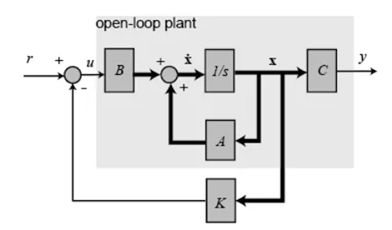
考虑未校正的单输入单输出系统，x可以是状态向量也可以是误差状态向量：

\dot{x}=Ax+Bu
y=Cx

线性状态反馈控制信号为:

u=-Kx=-\left[k_1,k_2,\ldots k_n\right]x

定义综合性能指标为:

J=\int_{0}^{\infty}\left(x^TQx+Ru^2\right)dt

{L_1=x}^TQx,Q是权重矩阵，定义Q的特征值为非负，即x^TQx\geq0。当x为误差状态向量时，L_1自然表示误差的大小；当x为状态向量时，也可以认为是x与0向量之间的误差。故L_1衡量误差的大小。当综合性能指标最小时，这一项也会要求尽量小。Q一般是对角矩阵，对角线上的元素取大于等于0的常量或时变量，对角线上每个元素的大小，表示可x的各元素在最优化时的权重，该数越大，则期望该状态分量误差越小。从效果来看，大权重的Q矩阵，能让状态量收敛更快。当某些元素取0，则表示对某些状态不做要求。
L_2=Ru^2中，R也是权重矩阵，u是控制输入。L_2衡量了控制付出的代价。
当K=R^{-1}B^TP时，性能指标J达到最小值。其中，P为n×n维的矩阵，满足

A^TP+PA-PBR^{-1}B^TP+Q=0

上式通常称为里卡蒂（Riccati）方程，适用于利用计算机编程的方式求得其数值解。

离散LQR实现步骤

离散化处理

\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)
y=Cx\left(t\right)+Du\left(t\right)

离散化为

x_{k+1}=A_dx_k+B_du_k
y_k=C_dx_k+D_du_k

状态空间系统离散化公式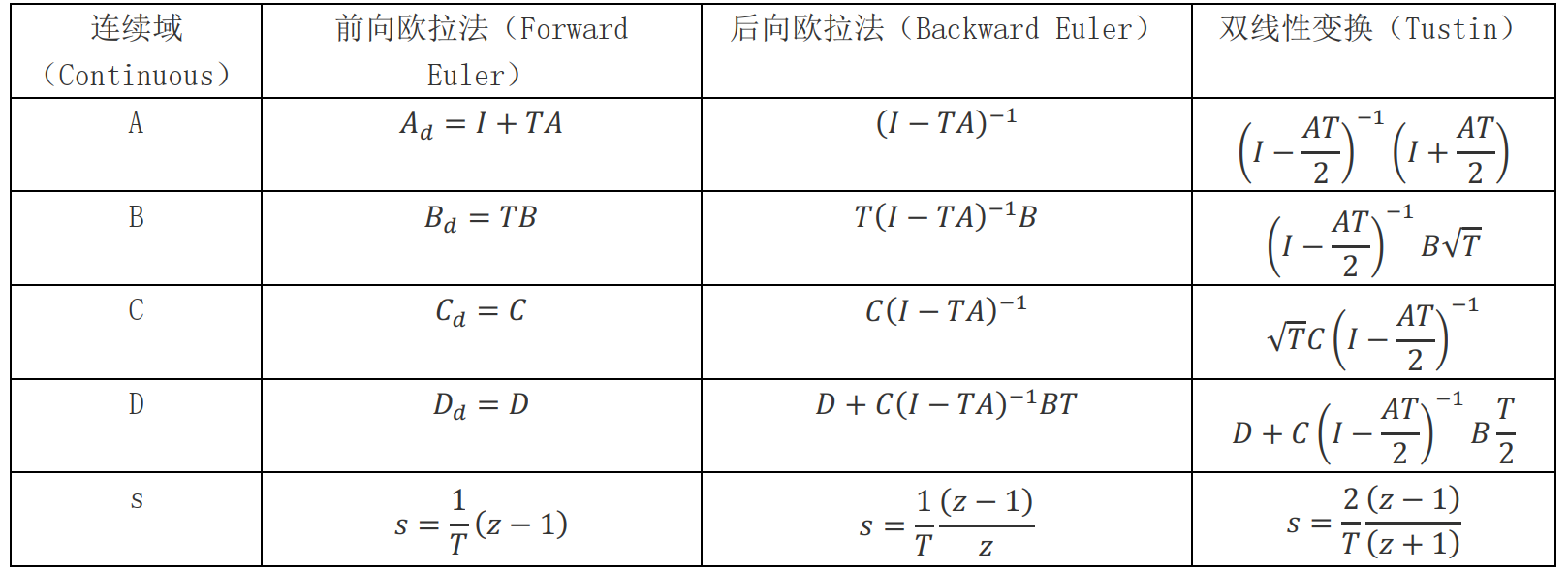
例：Apollo离散化采用前向欧拉法和双线性变换法两种方法。
离散后的，当K=\left(R+B_d^TPB_d\right)^{-1}B_d^TPA_d时，性能指标J最小。其中矩阵P需要满足里卡蒂方程：

P=A_d^TPA_d-A_d^TPB_t\left(R+B_d^TPB_d\right)^{-1}B_t^TPA_d

所以设计离散LQR控制器需要求取反馈矩阵K，计算过程十分工程化：
选择参数矩阵Q和R；
根据Riccati方程求解矩阵P, 在Matlab和代码实现中均有成熟的计算方法，不必深究其原理
计算反馈矩阵K=\left(R+B_d^TPB_d\right)^{-1}B_d^TPA_d

参考《现代控制理论 第三版》第六章 最优控制