按照我们的初级进阶之路，位置搞定了，下一步该是速度了。

速度可以表示为位置的微分形式，所以对机器人的微分运动分析就可以进行速度分析。

雅可比矩阵

首先我们求速度，一般指的是机械臂端部的速度。所以对端部位姿求微分，可写为  。其中  为末端沿xyz轴的微分运动，  为末端绕xyz的微分旋转。而我们也已经知道端部位姿矩阵关于关节变量的方程，例如

对其求时间微分，等式右边对关节变量  求导，可得到

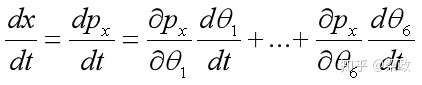
去掉dt，可得

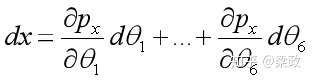
那么，用同样的方式计算  ，可得相同形式，总结为如下

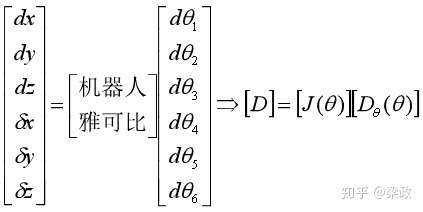
其中矩阵  为机器人的雅可比矩阵（Jacobian）。它描述了一种关系，可以将转动关节的微分运动表示成末端关节的微分运动。注意，雅可比矩阵不是常数矩阵，他随着关节角变化而变化。

像正逆运动学一样，知道了转动关节，也就是电机的角速度，我们就可以求出末端关节的位姿变化速度；另一方面，有了对位姿变化速度的要求，就可以对电机角速度进行设计。

这次就不手撕雅可比了，直接上代码吧。假设我们的  ，看看雅可比矩阵和位姿增量为多少。

用rbt的话直接robot.jacob0(theta_d)。

L(1)=Link('d',105.03,'a',0,'alpha',pi/2,'standard'); 
L(2)=Link('d',0,'a',-174.42,'alpha',0,'offset',-pi/2,'standard');
L(3)=Link('d',0,'a',-174.42,'alpha',0,'standard');
L(4)=Link('d',75.66,'a',0,'alpha',pi/2,'offset',-pi/2,'standard');
L(5)=Link('d',80.09,'a',0,'alpha',-pi/2,'standard');
L(6)=Link('d',44.36,'a',0,'alpha',0,'standard');  
robot=SerialLink(L(1:6),'name','Gluon_6L3', 'manufacturer','innfos')
theta=deg2rad(15*ones(6,1));
T=robot.fkine(theta).T;
D_theta = deg2rad(0.1*ones(6,1));
J = robot.jacob0(theta)  %Jacob Matrix
D = J*D_theta

结果为

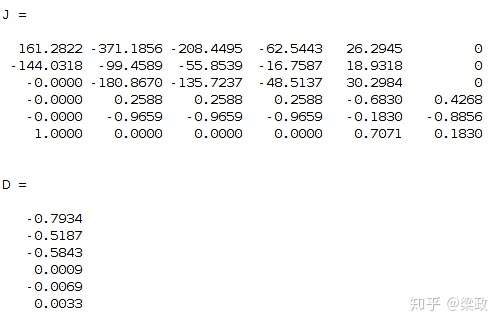
这里  表示的6自由度位姿的增量。

微分变换

在得到位姿的增量后，我们还应该求得位姿T矩阵的增量  和变换后的位姿T矩阵  。

按照基础T矩阵坐标变换，位姿矩阵增量应该是根据位姿得坐标变换得来的。我们的位姿增量[D]为微分形式，所以叫微分变换。

微分平移， ；

微分旋转，

因为是微分项，所以求可近似。近似后旋转顺序可忽略，这样旋转可认为是绕k轴旋转d_theta角，再将高阶项省略。由微分旋转可得变换后的矩阵

I为单位阵，我们称  为微分算子。

归纳一下，微分算子为

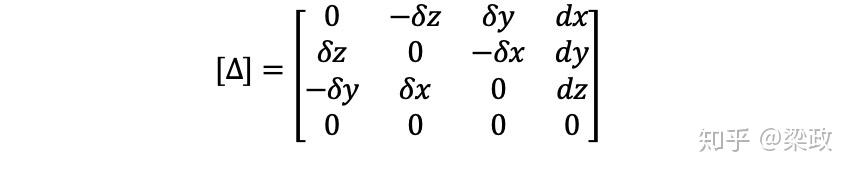
然而，此处的  表示的是相对于固定参考坐标系的微分算子。还有其他微分算子，比如相对于当前坐标系的微分算子  。这个之后要用到，所以要求一下。

相对于固定的左乘，相对于当前的就要右乘。结果应该是一样的，以为描述的相同的变化。所以

归纳一下，相对于当前坐标系的微分算子为

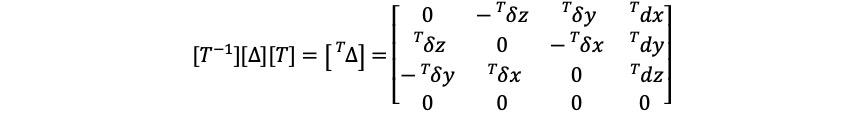
其中

 ，，  ，

，  ， 。

这样我们就可以利用关节转角微分->雅可比矩阵->位姿微分->微分算子->末端微分运动位姿矩阵dT->末端位姿矩阵

我们利用matlab求一下

% 接上部分
delta = [0   -D(6)  D(5) D(1);
         D(6) 0    -D(4) D(2);
        -D(5) D(4)  0    D(3);
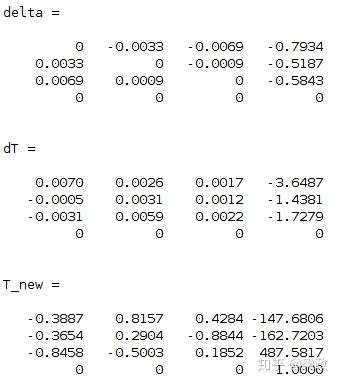
         0    0     0    0]    %微分算子
dT = delta*T      
T_new = dT+T

结果如下