主要记录一下，概率公式，先验、后验、似然等概念，并记录对贝叶斯滤波、离散贝叶斯滤波、静态二值贝叶斯滤波、粒子滤波的理解过程。

一、条件概率，条件独立联合概率

1.1 条件概率与联合概率的概念

条件概率是指事件A在事件B已经发生的条件下发生的概率。条件概率表示为：P(A|B)，读作“A在B发生的条件下发生的概率”。
联合概率是指在多元的概率分布中多个随机变量分别满足各自条件的概率。表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者 P(A,B),或者 P(A∩B)。

1.2 独立与相关、贝叶斯准则

A与B两个事件独立时，情况比较简单，这个时候条件概率 P(A|B) = P(A), 联合概率 P(A,B) = P(A)*P(B)

我们主要研究A与B两个事件相关的情况。
此时条件概率：P(A|B) = P(A,B)/P(B)
联合概率：P(A,B) = P(A|B)_P(B)，P(B,A) = P(B|A)_P(A)

由 P(A,B) = P(B,A)可以得到： P(A|B)_P(B) = P(B|A)_P(A)
即： P(A|B) = P(B|A)*P(A)/P(B)
就得到了贝叶斯准则的公式。

1.3 为贝叶斯准则带入全概率公式

全概率的意义在于，直接求 P(B) 十分困难，所以我们记录每一次事件 A 发生而导致 B 发生的概率，并全部加起来就是全概率公式。
注意每一次，也就是说我们假想的是一个完整的覆盖所有情况的样本空间，对应下面的完备事件组
若事件 A1，A2，…An 构成一个完备事件组且都有正概率，则对任意一个事件 B，有如下公式成立：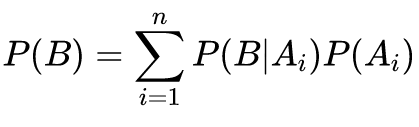

在全概率公式的总结下，贝叶斯准则公式可以表示为：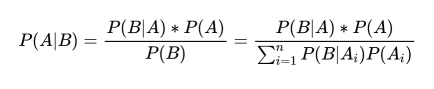

在应用中，A是一个希望通过B推测出来的数值（事件），这里有几个名词。

1. 后验概率：P(A|B)
2. 似然概率：P(B|A)
3. 先验概率：P(A)

观察全概率公式下的贝叶斯准则，其意义就是：利用“逆”条件概率（似然概率P(B|A)）和先验概率P(A)一起计算得到后验概率P(A|B)。
抽象上理解，把B看做传感器数据，A看做机器人状态，我们可以理解为：
P(A|B)表示要从传感器数值B推断得到机器人状态A，P(A)表示上一次（或者从上一次估计）得到机器人的状态，P(B|A)表示机器人状态为A时得到数据B的概率。
在机器人学中，概率P(B|A)经常被称为生成模型，因为在一定的抽象层面上，它表示状态变量如何引起了检测数据的变化。（—-概率机器人）

需要注意的是：

1. 分母的下标n表示一个完备事件组，与在什么时刻无关，理想的 n 即代表样本空间的所有划分。通俗点讲就是说P(B)不依赖A，公式里的1/P(B)对任何A的后验P(A|B)都是相同的，通常由 η 表示。
2. η是一个归一化因子，它表示所有可能的概率之和等于1，比如硬币的正反面，若在某一时刻得到正面置信度为0.3η、反面置信度为0.1η，那么η可以通过0.3η+0.1η=1得到。
   贝叶斯准则公式可进一步被表示为：P(A|B) = η_P(B|A)_P(A)

综合以上描述，贝叶斯法则可以表示为：后验概率 = (似然概率 * 先验概率)/标准化常量

1.4 最大后验（MAP）与最大似然（MLE）

参考：https://blog.csdn.net/u011508640/article/details/72815981/

最大似然估计（Maximum likelihood estimation, 简称MLE）：
假设有一个造币厂生产某种硬币，现在我们拿到了一枚这种硬币，想试试这硬币是不是均匀的。即想知道抛这枚硬币，正反面出现的概率（记为 θ）各是多少？
于是我们拿这枚硬币抛了10次，得到的数据是：反正正正正反正正正反。我们想求的正面概率 θ 是模型参数，而抛硬币模型我们可以假设是二项分布。在这七次测量里，f(θ) = θ^7 . (1−θ)^3
然后我们把 f(θ) = θ^7 . (1−θ)^3 当做模型，画出其 f(θ) 的图像：

f = zeros(10, 1);
n = zeros(10, 1);
for t = 1:10
    n(t) = t/10;
    f(t) = n(t)^7 * (1-n(t))^3;
end
plot(n, f);
xlabel('θ');
ylabel('likelihood value');

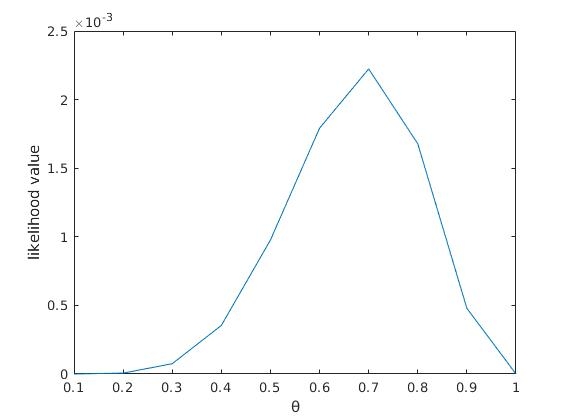
可以看出，在 θ = 0.7时，似然函数取得最大值。

这样，我们已经完成了对 θ 的最大似然估计。即，抛10次硬币，发现7次硬币正面向上，最大似然估计认为正面向上的概率是0.7。

最大后验概率估计（Maximum a posteriori estimation, 简称MAP）：
接着刚刚的抛硬币问题：一些人可能会说，硬币一般都是均匀的啊！ 就算你做实验发现结果是“反正正正正反正正正反”，我也不信 θ = 0.7 。
这里就包含了贝叶斯学派的思想了——要考虑先验概率。 为此，引入了最大后验概率估计。

对于投硬币的例子来看，我们认为“先验地知道” θ取0.5的概率很大，取其他值的概率小一些。然后开始套贝叶斯准则……

二、条件独立， 概率生成法则

2.1 条件独立

以上推导都是两个事件条件，接下来添加任意变量（事件）Z
需要注意的是：

1. 在做P(X,Y|Z)、P(X|Y,Z)这类概率的理解和运算时，先求联合再做条件概率（这个说法可能不准确）。
   条件概率里面形如的“B|A”这样的表示，根本就不是一个事件，它无法被当作一个事件来定义。
2. P(X,Y|Z)表示：在Z发生时，X、Y同时发生的概率。
3. P(X|Y,Z)表示：在Y和Z同时发生时，X发生的概率。

条件独立定义：
定义：如果 P(X,Y|Z)=P(X|Z)P(Y|Z)，或等价地 P(X|Y,Z)= P(X|Z），则称事件X,Y对于给定事件Z是条件独立的，也就是说，当Z发生时，X发生与否与Y发生与否是无关的。
注意，这并不意味着X与Y是独立的，相反它的意义就是：事件Z的发生，使本来可能不独立的事件X和事件Y变得独立起来。
总结来看就是P(X|Z)、P(Y|Z)满足相互独立，而P(X)、P(Y)并不确定是否满足相互独立
关于条件独立的抽象理解以及证明，我们可以参照百度百科：https://baike.baidu.com/item/%E6%9D%A1%E4%BB%B6%E7%8B%AC%E7%AB%8B%E6%80%A7/22368188?fr=aladdin

2.2 概率生成法则

我们假设机器人首先执行一个动作 u ，然后得到一个测量 z ，机器人的实际状态为 x
并且是一个满足一阶马尔可夫性的过程：t 时刻的状态概率只取决于 t-1 时刻，意味着时刻 t 状态足以代表过去的总结，来预测未来状态。
假设 x 是完整的，那么它是所有以前时刻发生的状态的充分总结，用 x(t-1) 可以代表从开始一直到 t-1 时刻的控制和测量的总和。
也就是说 x(t) 只关注 x(t-1)，而不会关注z(0:t-1)、u(0:t-1)、x(0:t-2)。
时刻t的状态随机地依赖t-1时刻的状态和控制u(t)；测量z(t)随机地依赖时刻t的状态，这样子的时间生成模型也称为隐马尔科夫模型（Hidden Markov Model，HMM） 或 动态贝叶斯网络（Dynamic Bayes Network，DBN）。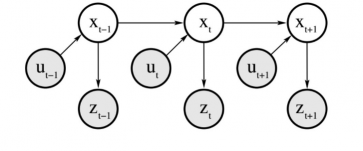

对于状态 x，机器人在 t 时刻的状态转移概率(State Transition Probability)为：P(x(t)) = P(x(t)|x(t-1),u(t))
对于测量 z，机器人在 t 时刻的测量概率(Measurement Probability)为：P(z(t)|x(0:t),z(1:t-1),u(1:t)) = P(z(t)|x(t))
注意这里的z和u都是从1时刻才开始有的，而不是0时刻。但x则是从0时刻就有的。所以确定初始的先验也比较重要，我们一般给定初始先验。

这里x(0:t-1),z(1:t-1),u(1:t)变为x(t-1),u(t)这种变换，其实是反映了条件独立的概念的，表示加入一个条件变量后，原有的条件变量独立于其它变量。
P(x(t)|x(t-1),u(t))表明可以通过 上一时间的状态量 和 当前时间的控制量 得到 当前时间的状态量。也就是控制量 u 是如何影响状态量 x 的。状态转移概率(State Transition Probability)
P(z(t)|x(t))表明可以通过 当前时间的的状态量 得到 当前时间的观测量。将观测 z 看做是状态 x 的有噪声的预测。测量概率(Measurement Probability)

在概率机器人中，机器人及其环境的动态以两种概率法则，即状态分布和测量分布的形式为特点。
状态转移分布描述状态如何随时间变化的特征可能作为机器人控制的效果。
测量分布描述测量如何由状态控制的特征。
两者都是概率性的，从而导致了状态演变和检测的固有不变性。—-《概率机器人》
贝叶斯滤波的推导过程这里不做叙述。

2.3 置信度

通过概率生成法则里的动态贝叶斯网络，可以知道：当前状态仅与控制量和上一状态有关，而与观测无关。
理所当然地，我们会想到通过观测来估计状态，置信度就是用来建立状态与观测的关系的，置信度的意思就是当前观测相比较于状态的可信程度。
置信度分布是以观测数据为条件的关于状态变量的后验概率，这个后验是 t 时刻状态 x 的概率分布，以所有过去测量z(1:t)和过去控制u(1:t)为条件。
x(t)的置信度（后验概率）表示为：bel(x(t)) = P(x(t)|z(1:t),u(1:t))
以上是综合了从 1 时刻到 t 时刻，得到 t 时刻观测 z(t) 之后的置信度（后验概率）
对于真实的状态，置信分布为每一个可能的假设分配一个概率。

而有时候在 t 时刻刚刚执行了控制 u(t) 后，综合观测 z(t) 之前（此时还没有得到z(t)）的置信度（后验概率），认为这个计算是有用处的：
其表示为 _bel(x(t)) = P(x(t)|z(1:t-1),u(1:t)) （_bel(x(t))的横线应该在上边，为了打字方便给挪左边去了）
计算_bel(x(t))的过程常常被称为预测，是基于以前状态的后验估计
在综合 t 时刻的测观测之前，预测了 t 时刻的状态。再由_bel(x(t))得到bel(x(t))的过程称为修正，或者测量更新(measurement update)

此即为贝叶斯滤波的基础。可以看到我们实际是求得 以观测数据为条件的关于状态变量的后验概率，所以在此基础上的贝叶斯滤波等算法，属于最大后验估计这一类问题。

2.4 非参数滤波概念

非参数滤波是高斯滤波的一种替代选择，非参数滤波不依赖于确定的后验函数，它是通过有限的数据来近似后验。近似的质量主要取决于表示后验数据的量，当数据量足够大的时候，往往会一致收敛于真实的后验值。
非参数滤波：直方图滤波（离散贝叶斯滤波）、粒子滤波。
高斯滤波：卡尔曼滤波系列。

三、 贝叶斯滤波

3.1 基本贝叶斯滤波算法

大多数计算置信度的方式都是通过贝叶斯滤波（Bayes filter）算法给出的。
推导过程这里不细述，具体可以去看《概率机器人》，或者其它地方的推导方式。
直接给出其算法程序，记住贝叶斯滤波的两步：

1. 预测prrediction（或者叫控制更新control update）：这个步骤的公式与全概率定理公式相呼应
   机器人分配状态x(t)的置信度_bel(x(t))，由分配给x(t-1)的置信度bel(x(t-1)) 和 由控制器u(t)引起的从t-1到t时刻的状态转移概率 的 积分得到。
2. 测量更新measurement update：这个步骤与贝叶斯准则公式相呼应
   用已经观测到的测量z(t)的概率（似然概率） 乘以 置信度_bel(x(t))（先验概率）得到最后的置信度（先验概率）bel(x(t))

这里有几个可能不是很准确的描述，将贝叶斯准则与贝叶斯滤波里的概率联系起来。
在贝叶斯滤波中，测量概率和似然概率都描述了观测（或测量）和状态之间的关系。 测量概率 实际表示的是观测数据和系统状态之间的似然关系，所以有时会被直接叫做 似然 。
在贝叶斯滤波的预测步骤中，上一时刻的置信度将会作为后续更新步骤中置信度bel(x(t))后验状态的先验。所以 上一时刻的置信度bel(x(t-1)) 有时会被直接叫做 先验 。有时我们也会把预测置信度叫做先验。
置信度分布是以观测数据为条件的关于状态变量的后验概率，所以测量更新得到的 置信度 有时会被直接叫做 后验 。
贴一下，我所理解的基本贝叶斯滤波公式里的各个名词位置：

对于以上程序：

1. 需要已知初始置信度bel(x(0))，因为贝叶斯滤波算法算法是递归进行的：t 时刻的置信度bel(x(t))是由 t-1 时刻的置信度bel(x(t-1))计算得到的。
   贝叶斯滤波算法分为两步：对每一时刻的状态量 x 都做一次预测得到 _bel(x(t))，然后再做一次测量更新得到 bel(x(t))。
2. η是一个归一化因子，它表示所有可能的概率之和等于1，比如硬币的正反面，若在贝叶斯滤波某一时刻得到正面置信度为0.3η、反面置信度为0.1η，那么η可以通过0.3η+0.1η=1得到。
3. 上式∫(…)d(…) 里的dx(t-1)，表示对上一时刻的所有状态进行积分，这就带来了问题。

贝叶斯滤波比较适用于有限状态空间的问题。

1. 对于有限状态空间的问题，贝叶斯滤波是一种非常有效的方法，并且相对容易转换为代码实现。由于状态空间是有限的，我们可以使用离散的概率分布或概率矩阵来表示状态和观测之间的转移概率，其应用方式如接下来要介绍的 离散贝叶斯滤波、静态二值贝叶斯滤波 和 粒子滤波器。例：判断门是开的还是关的，其状态空间只有两种情况，开和关。
2. 对于无限状态空间问题，则不适合用贝叶斯来估计，在无限状态空间中，由于状态的数量是无穷的。对对上一时刻的所有状态进行积分是办不到的事情，通常会考虑使用其他类型的滤波器或估计方法，如 KF、EKF、UKF、IF、EIF这类高斯滤波器。例：判断某一个变量的值，这个值可以是任意的数，其状态空间就是无限的。

四、离散贝叶斯滤波算法

4.1 算法理解

1. 对于有限（少量）状态空间的问题，贝叶斯滤波是一种非常有效的方法。

2. 输入：上一时刻的置信度(先验)bel(x(t-1))、测量概率(似然)p(z(t)|x(t))、状态转移概率P(x(t)|x(t-1),u(t))，输出：当前时刻的置信度(后验)bel(x(t))。

3. 需要确定初始置信度。

4. 要注意状态空间的维度。

4.2 实例：机器人开门问题

以经典的机器人开门问题为例，来源于《概率机器人》：

1. 假设门只有两种状态，开和关，且只有机器人能够改变门的状态；

2. 机器人不知道门的初始状态，用相同的先验概率作为初始置信度，bel(X0 = open)=0.5，bel(X0 = close)=0.5;

3. 机器人通过传感器观测门的状态，传感器具有噪声，传感器在门打开的情况下有0.6的概率得到正确结果、在门关闭时传感器有0.8的概率得到正确结果。
   也就是说，噪声特性下的观测概率表示为：
   P(Z=sense_open | X=open) = 0.6
   P(Z=sense_open | X=closed) = 0.2
   P(Z=sense_closed| X=open) = 0.4
   P(Z=sense_closed| X=closed) = 0.8

4. 只有机器人能改变门的状态，机器人通过传感器观测推断门的状态。
   push操作的意思是：若门是开着的则保持门开着（不施加控制量）、若门是关着的则施加一个控制量开门。
   那么状态转移概率可以表示为：
   第一种情况，Ut=nothing：
   p(Xt=open | Ut=nothing, X(t-1)=open) = 1 // 在门打开的情况下，不进行任何操作，门变为打开的概率为1
   p(Xt=open | Ut=nothing, X(t-1)=closed) = 0 // 在门关闭的情况下，不进行任何操作，门变为打开的概率为0
   p(Xt=closed | Ut=nothing, X(t-1)=open) = 0 // 在门打开的情况下，不进行任何操作，门变为关闭的概率为0
   p(Xt=closed | Ut=nothing, X(t-1)=closed) = 1 // 在门关闭的情况下，不进行任何操作，门变为打开的概率为1
   第二种情况，Ut=push：
   p(Xt=open | Ut=push, X(t-1)=open) = 1 // 在门打开的情况下，进行push操作，门变为打开的概率为1
   p(Xt=closed | Ut=push, X(t-1)=open) = 0 // 在门打开的情况下，进行push操作，门变为关闭的概率为0
   p(Xt=open | Ut=push, X(t-1)=closed) = 0.8 // 在门关闭的情况下，进行push操作，门变为打开的概率为0.8（传感器有0.8的概率判断正确，然后打开门）
   p(Xt=closed | Ut=push, X(t-1)=closed) = 0.2 // 在门关闭的情况下，进行push操作，门变为关闭的概率为0.2（传感器有0.2的概率判断错误，没有打开门）

5. 观测结果从0时刻到n时刻表示为observations = [1, 1, 2, 1, 1]; % 1表示门是开的，2表示门是关的

6. 该问题的目标是，根据观测结果，实时推断门的状态（或者说处于开或关的概率）

4.3 手动的求解过程：

1. t0时刻：
   初始置信度：bel(X0 = open)=0.5，bel(X0 = close)=0.5。

2. t1时刻：机器人不使用操作器，检测到门的状态是开着的。Z1=sense_open，U1=nothing
   1).上一时刻的置信度为：bel(X0 = open)=0.5，bel(X0 = close)=0.5
   2).状态转移概率（第一种情况，Ut=nothing）：

    p(X1=open   | U1=nothing, X0=open)   = 1
    p(X1=open   | U1=nothing, X0=closed) = 0
    p(X1=closed | U1=nothing, X0=open)   = 0
    p(X1=closed | U1=nothing, X0=closed) = 1
   

   3).预测prrediction：

    _bel(X1=open)   = p(X1=open   | U1=nothing, X0=open) * bel(X0=open) + p(X1=open   | U1=nothing, X0=closed) * bel(X0=closed) = 1*0.5+0*0.5 = 0.5
    _bel(X1=closed) = p(X1=closed | U1=nothing, X0=open) * bel(X0=open) + p(X1=closed | U1=nothing, X0=closed) * bel(X0=closed) = 0*0.5+1*0.5 = 0.5
   

   4).测量更新measurement update

    bel(X1=open)   = η * p(Z1=sense_open | X1=open)   * _bel(X1=open)   = η*0.6*0.5 = 0.3η
    bel(X1=closed) = η * p(Z1=sense_open | X1=closed) * _bel(X1=closed) = η*0.2*0.5 = 0.1η
    0.3η + 0.1η = 1
    bel(X1=open)   = 0.75
    bel(X1=closed) = 0.25
   

3. t2时刻：机器人使用操作器把门拉开，检测到门是开着的。U2=push，Z2=sense_open
   1).上一时刻的置信度为：bel(X1 = open)=0.75，bel(X1 = close)=0.25
   2).状态转移概率（第二种情况，Ut=push）：

    p(X2=open   | U2=push, X1=open)   = 1
    p(X2=closed | U2=push, X1=open)   = 0
    p(X2=open   | U2=push, X1=closed) = 0.8
    p(X2=closed | U2=push, X1=closed) = 0.2
   

   3).预测prrediction：

    _bel(X2=open)   = p(X2=open   | U2=push, X1=open) * bel(X1=open) + p(X2=open   | U2=push, X1=closed) * bel(X1=closed) = 1*0.75+0.8*0.25 = 0.95
    _bel(X2=closed) = p(X2=closed | U2=push, X1=open) * bel(X1=open) + p(X2=closed | U2=push, X1=closed) * bel(X1=closed) = 0*0.75+0.2*0.25 = 0.05
   

   4).测量更新measurement update

    bel(X2=open)   = η * p(Z2=sense_open | X2=open)   * _bel(X2=open)   = η*0.6*0.95 = 0.57η
    bel(X2=closed) = η * p(Z2=sense_open | X2=closed) * _bel(X2=closed) = η*0.2*0.05 = 0.01η
    0.57η + 0.01η = 1
    bel(X1=open)   = 0.983
    bel(X1=closed) = 0.017
   

   至此，求解过程已经走了两步，后面步骤类似，在问题一开始我们知道了 初始置信度 和 状态转移概率，然后在每一步的时候确定控制量U、观测量Z、上一时刻的置信度，从而更新当前置信度

4.4 matlab代码验证：

% 机器人开门的贝叶斯滤波器示例
% 初始化状态和观测参数
% 初始状态，门开和门关的概率均为0.5，对应：
% bel(X0 = open)=0.5，
% bel(X0 = close)=0.5;
initialState = [0.5; 
                0.5]; 

% Ut=nothing的状态转移矩阵，对应：
% p(Xt=open   | Ut=nothing, X(t-1)=open), p(Xt=open   | Ut=nothing, X(t-1)=closed);
% p(Xt=closed | Ut=nothing, X(t-1)=open), p(Xt=closed | Ut=nothing, X(t-1)=closed)   
transitionMatrix_no = [1.0, 0.0; 
                       0.0, 1.0];

% Ut=push的状态转移矩阵，对应：
% p(Xt=open   | Ut=push, X(t-1)=open), p(Xt=open   | Ut=push, X(t-1)=closed);
% p(Xt=closed | Ut=push, X(t-1)=open), p(Xt=closed | Ut=push, X(t-1)=closed)  
transitionMatrix_pu = [1.0, 0.8; 
                       0.0, 0.2];

% Z1=sense_open的观测矩阵，对应：
% P(Z=sense_open  | X=open) = 0.6
% P(Z=sense_open  | X=closed) = 0.2
observation_open = [0.6;
                    0.2];

% Z1=sense_closed的观测矩阵，对应：
% P(Z=sense_closed| X=open) = 0.4
% P(Z=sense_closed| X=closed) = 0.8
observation_clos = [0.2;
                    0.8];  

% 不同时刻传感器的观测结果
% 1表示门是开的，0表示门是关的
observations = [1, 1, 0, 0, 0];

% 不同时刻的控制方式
% 1表示push，0表示nothing
pushcontrol = [0, 1, 1, 1, 1];


% 初始化滤波器
filterState = initialState;

% 预先分配用于存储滤波结果的变量
filteredStates = zeros(2, length(observations)+1);
filteredStates(:, 1) = filterState;

% 贝叶斯滤波循环
for i = 1:length(observations)
    % 在这个实例里面，t1时刻不使用操作器，U1=nothing
    if pushcontrol(i) == 0
        % 预测步骤prrediction
        predictedState = transitionMatrix_no * filterState;

        % 更新步骤measurement update
        observation = observations(i);% 取出此时刻的观测结果
        if observation == 1
            likelihood = observation_open;
        elseif observation == 0
            likelihood = observation_clos;
        end


        filterState = likelihood .* predictedState;
        filterState = filterState / sum(filterState);  % 归一化

        % 存储滤波结果
        filteredStates(:, i+1) = filterState;

    % 在这个实例里面，除开t1时刻外，都使用操作器，U(t)=push
    else
        % 预测步骤prrediction
        predictedState = transitionMatrix_pu * filterState;

        % 更新步骤measurement update
        observation = observations(i);% 取出此时刻的观测结果
        if observation == 1
            likelihood = observation_open;
        elseif observation == 0
            likelihood = observation_clos;
        end


        filterState = likelihood .* predictedState;
        filterState = filterState / sum(filterState);  % 归一化

        % 存储滤波结果
        filteredStates(:, i+1) = filterState;
    end
end

% 绘制滤波结果
timeSteps = 1:length(observations)+1;
plot(timeSteps, filteredStates(1, :), 'ro-', timeSteps, filteredStates(2, :), 'bo-');
legend('门开的概率', '门关的概率');
xlabel('时间步');
ylabel('概率');
title('机器人开门的贝叶斯滤波结果');

4.5 结果分析：

通过matlab得到的结果为：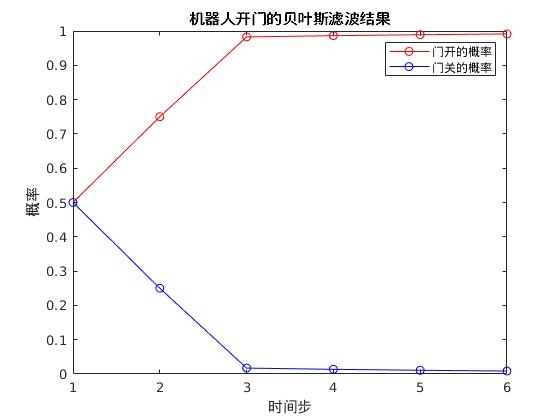

由于我们在除第一步后都有push动作，所以后面的门的状态会越来越趋向与开着。
我们可以改变observations = [1, 1, 0, 0, 0];和pushcontrol = [0, 1, 1, 1, 1];会得到不同的结果。

五、静态二值贝叶斯滤波算法

5.1 算法理解

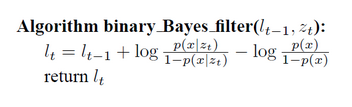
log()表示以e为底的对数

1. 静态二值贝叶斯滤波显然有两个关键词，一个是静态，一个是二值：
   静态就是状态的后验概率与控制数据无关，也就是没有控制量 u ；二值就是后验是一个二值数，也就是状态 x 只有两种情况，且先验概率和为1，即: p(x) + p(~x) = 1。

2. 由于状态是二值的，某个状态发生的概率与某个状态不发生的概率是互为相反数的，所以一般只更新一种状态的概率表示
   例如栅格地图算法里，栅格状态只有空闲x=0和占据x=1，若它非常趋近于占据，则说明它非常不趋近于空闲。
   所以，我们只更新占据x=1状态的后验表示即可，这样子就把状态空间从2维降到1维了，这也是此算法的优点。
   如果不理解，参考下面的例子里，我们只讨论占据状态的各种概率，p(x|z=free)就是p(x=1|z=free)，p(x)就是p(x=1)，而不考虑p(x=0|z=free)、p(x=0)什么的

3. 输入：一次观测的后验概率p(x(t)|z(t))、先验概率p(x(t))、上一时刻置信度l(t-1)；输出：若干次观测后的置信度l(t)；置信度初值(t0)由先验得到
   它的置信度输出不在是一个[0,1]的概率了，其值域实数域，越大表示越趋向该状态，我们用符号 l 来表示
   l(t)在0时刻的初始值，一般取先验计算，l(t0)=log(p(x)/(1-p(x)))

4. 静态二值贝叶斯滤波利用一个反向测量模型 (实际上就是这次观测的后验概率) p(x|z) ，代替熟悉的前向测量模型(实际上就是似然概率) p(z|x)：
   反向测量模型经常用于测量比二值状态更复杂的情况，比如说根据相机图片判定门的开关状态，状态十分简单，但是测量空间却十分庞大。 相比于已知门的状态来估计所有图像出现的概率，我们更容易找到一个函数来根据图像判定门是否开着，在这种情况下反向测量模型要比前向测量模型更容易实现。

5. 所以此算法神奇之处在于认为我们可以轻易得到每次观测的后验，但是要从从若干次的观测后验里，得到一个最终认为可信的、某一状态的置信度：
   在离散贝叶斯里，后验就是置信度，但是这里不一样，当然这个置信度也是由后验所表示的，只不过取了对数。
   比如栅格地图算法里，观测扫到为占据的表达为 z = occupyde，观测扫到为空闲的表达为 z = free（这里只是举例，总之从z我们可以明显知道栅格是否被占据就对了）。z = occupyde 就表示它大概率占据（后验：p(x|z=occupyde)=0.7）,z = free 就表示它大概率空闲（这次观测的后验：p(x|z=free)=0.3 ）

5.2 实例：简单栅格地图更新问题

参考《概率机器人》第九章第二节：占用栅格地图构建算法

1. 假设有10*10大小的二维栅格地图，栅格地图的状态是二值形式：占据x=1、空闲x=0
2. 每个栅格的初始状态为，一半概率占据一半概率空闲，也就是先验概率：p(x)=0.5。这个实例还挺特殊，当然我们也可以设置为其它的先验。
3. 对地图的所有栅格我们有许多组观测到的数据，为了方便这里把 z = occupyde 表示为 z = 10，此时大概率占据；把 z = free 表示为 z = -10此时大概率空闲。其反向测量模型（这次观测的后验概率）： p(x|z=10)=0.7，p(x=0|z=10)=0.3 , p(x|z=-10)=0.4，p(x=0|z=-10)=0.6
4. 需要结合这许多组的不同观测数据，更新栅格地图内每个栅格的占据情况

5.3 手动的求解过程：

若某个栅格t1时刻第一次观测为10，t1时刻第二次观测为-10，t1时刻第三次观测为10，t1时刻第四次观测为10

1. 首先每个栅格的先验概率：p(x)=0.5、p(x=0)=1-p(x)=0.5。
   那么有log(p(x)/(1-p(x))) = 0
2. 然后确定反向测量模型（每次观测的后验概率）： p(x|z=10)=0.7，p(x|z=-10)=0.4
3. t0初始时刻，l(t0)=log(p(x)/(1-p(x))) = 0
4. t1时刻，观测为10，则l(t1)=l(t0) + log(p(x|z=10)/(1-p(x|z=10))) - 0 = 0+log(7/3)+0 = log(7/3) = 0.8473
5. t2时刻，观测为-10，则l(t2)=l(t1) + log(p(x|z=-10)/(1-p(x|z=10))) - 0 = log(7/3)+log(4/6)+0 = log(14/9)= 0.4418
6. t3时刻，观测为10，则l(t3)=l(t4) + log(p(x|z=10)/(1-p(x|z=10))) - 0 = log(14/9)+log(7/3)+0 = log(98/27)= 1.2891
7. t4时刻，观测为10，则l(t4)=l(t3) + log(p(x|z=10)/(1-p(x|z=10))) - 0 = log(98/27)+log(7/3)+0 = log(686/81)= 2.1364
8. 后面步骤类似。

5.4 matlab代码验证：

% 创建地图
mapSize = [10, 10];  % 地图尺寸（栅格数量）
occupancyMap = zeros(mapSize);

% 先验概率
p_x=0.5;

% 初始状态
log_prior = log(p_x/(1-p_x));

% 根据初始状态更新地图
occupancyMap = ones(size(occupancyMap)) * log_prior;


% 反向测量模型（每次观测的后验概率）
observation_occu = 0.7;  % z = occupyde 表示为 z = 10，此时大概率占据 p(x|z=10)=0.7，p(x=0|z=10)=0.3
observation_free = 0.4;  % z = occupyde 表示为 z = -10，此时大概率空闲 p(x|z=-10)=0.4，p(x=0|z=-10)=0.6
% 取log(p(x|z)/(1-p(x|z)))
log_obs_occu = log(observation_occu/(1-observation_occu));
log_obs_free = log(observation_free/(1-observation_free));


% 定义多组观测数据（每组观测数据为一个二维数组，0表示空闲，1表示占用）
observations = {
    [ 10, -10, -10, -10,  10,  10,  10, -10, -10, -10;
     -10, -10, -10, -10,  10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10, -10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10, -10,  10,  10,  10,  10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;];

    [-10, -10, -10, -10, -10,  10, -10,  10, -10, -10;
     -10, -10, -10, -10,  10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10,  10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10, -10,  10,  10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;];

    [ 10, -10, -10, -10, -10, -10,  10, -10, -10, -10;
     -10, -10, -10, -10,  10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10,  10,  10,  10, -10,  10, -10;
     -10, -10, -10, -10,  10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10,  10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;];

    [ 10, -10, -10, -10, -10,  10, -10,  10, -10, -10;
     -10, -10, -10, -10,  10, -10,  10,  10, -10, -10;
     -10, -10, -10, -10,  10,  10, -10,  10,  10, -10;
     -10, -10, -10, -10,  10,  10,  10, -10, -10, -10;
     -10, -10, -10, -10, -10,  10,  10,  10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;
     -10, -10, -10, -10, -10, -10, -10, -10, -10, -10;]
};


% 静态贝叶斯滤波更新地图
% 在栅格地图更新中，常常使用取对数的方式来处理占用概率，以便进行更方便的计算和表示。
% 通过取对数，可以将乘法运算转换为加法运算，简化了贝叶斯滤波算法中的更新步骤。
for k = 1:numel(observations)
    observationData = observations{k};
    for row = 1:mapSize(1)
        for col = 1:mapSize(2)
            % 获取当前栅格的对数概率
            lastBelief = occupancyMap(row, col);

            % 根据观测数据进行更新
            observation = observationData(row, col);
            if observation > 0
                log_posterior = log_obs_occu;
            else
                log_posterior = log_obs_free;
            end
            updatedBelief = lastBelief + log_posterior + log_prior;

            % 更新栅格的对数概率
            occupancyMap(row, col) = updatedBelief;
        end
    end
end



% 显示生成的占用栅格地图
figure;
heatmap(occupancyMap);
title('Occupancy Grid Map');


% % 显示生成的占用栅格地图
% figure;
% colormap('gray');
% imagesc(occupancyMap);
% colorbar;
% title('Occupancy Grid Map');
% % 在每个栅格上显示对应的值
% for row = 1:mapSize(1)
%     for col = 1:mapSize(2)
%         text(col, row, sprintf('%.2f', occupancyMap(row, col)), 'Color', 'r', 'FontSize', 8, 'HorizontalAlignment', 'center');
%     end
% end

5.5 结果分析：

通过matlab得到的结果为：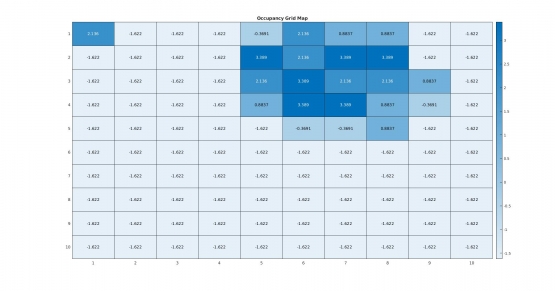

可以看到第一个栅格对应刚刚手动解算的部分。
我们可以尝试改变先验概率p_x=0.5;、反向测量模型（每次观测的后验概率）observation_occu = 0.7; observation_free = 0.4;、观测数据observations = {}，改变这些内容，会得到不同的结果。

六、 粒子滤波算法

6.1 算法理解

1. 粒子滤波的主要思想是，用一系列从后验得到的随机状态采样，表示后验。
   这些后验分布的样本叫做粒子（particles），一个粒子就是根据真实世界状态在时刻t的一种状态 x 的假设。

2. 输入：上一时刻的粒子集X(t-1)、测量概率(似然)p(z(t)|x(t))、状态转移概率P(x(t)|x(t-1),u(t))，这里其实是每个粒子的测量概率、状态转移概率。输出：当前时刻的粒子集X(t)。

3. 上图伪代码里，M表示总的粒子数，m表示某一粒子的序号；大写的X表示某一时刻的粒子集X(t)，小写的x表示某一粒子集里的粒子x(t)^m，有X(t): = x(t)^1, x(t)^2, x(t)^3, x(t)^4 …… x(t)^M ；
   理想状态下，某一粒子对应的状态假设x(t)^m包含在粒子集X(t)中的可能性与其贝叶斯滤波的后验成比例，即：x(t)^m ~ p(x(t)|z(t), u(t), x(t-1) )
   上图伪代码里第2行，先构建一个假想的粒子集，又叫暂时粒子集_X(t)。同时将最终粒子集X(t)一并初始化了。
   这一步相当于为贝叶斯滤波提供先验

4. 上图伪代码里第4行，基于粒子x(t-1)^m和控制u(t)产生时刻t的假想状态x(t)^m。所得样本用m标注，表示它是由X(t-1)中的第m个粒子产生的。这一步包括从状态转移概率p(x(t)|u(t), x(t-1))中采样，得到的粒子集就是_bel(x(t))。
   这一步与贝叶斯滤波的预测步骤（得到预测置信度_bel(x(t))）类似

5. 上图伪代码里第5行、第6行，为每个粒子x(t)^m计算所谓的重要因子（important factor），也就是粒子的权重，用w(t)^m表示。重要性是测量z(t)在粒子x(t)^m下的概率，用 w(t)^m = p(z(t)|x(t)^m) 给定。这个权重其实就是似然。
   然后对粒子集每个粒子更新其权重。如果将w(t)^m解释为每个粒子的权值，那么加权后的粒子集就近似代表了后验bel(x(t))。
   这步与贝叶斯滤波的测量更新步骤（得到后验置信度bel(x(t))）类似

6. 这个权重的计算方式，需要我们自己定义。常见的计算权重（Weight Calculation）方法有以下两种：
   1). 概率密度函数（PDF）计算： 假设观测数据服从某种概率分布，可以通过计算粒子预测状态在该分布下的概率密度函数值作为权重。常见的概率分布有高斯分布、均匀分布等。
   2). 残差计算： 通过计算粒子预测状态与观测数据之间的残差（预测值与实际值之间的差异），并根据残差的大小来确定权重。一般情况下，较小的残差对应较高的权重，可以使用欧氏距离或其他相似度度量来计算残差。
   3). 归一化权重（Weight Normalization）:为了确保权重的总和为1，需要对权重进行归一化处理。将所有粒子的权重除以所有粒子权重的总和，得到归一化后的权重。

7. 上图伪代码里第8-11行，，实现了重采样（resampling）或者叫重要性采样（importance sampling）。
   算法从暂时粒子集_X(t)里抽取替换M个粒子，抽取某个粒子的概率由其权重（重要因子）给定，重采样将M个粒子的粒子集变换成同样大小的粒子集。
   通过将重要性权重合并到采样过程，粒子的分布会发生变化：在重采样前，他们按照预测置信度_bel(x(t))分布；在重采样后，他们近似按照后验bel(x(t)) = η . p(z(t)|x(t)) . _bel(x(t))分布。
   注意这里说的是粒子的分布，是不考虑粒子其权重的，我们正是通过权重，将粒子进行重新分布，可以理解为这个过程就是尽量保留权重大的剔除权重小的粒子。
   事实上，得到的样本集通常有许多重复，因为粒子是替换得到的，不包含在最终粒子集X(t)中的粒子往往就是具有较低权重的粒子。

8. 重采样对迫使粒子回归后验分布有重要作用，说白了就是让粒子分布在其更可能出现的地方，粒子滤波也可以不进行重采样。
   粒子滤波也可以不进行重采样，而是为每一个粒子维护一个权重，权重初始化为1，并按照 w(t)^m = p(z(t)|x(t)^m) . w(t)^m 进行更新。这样子算法仍然能够近似后验，但其中的粒子没有被更新，有一些粒子最终的后验概率会非常低，我们最终取其权重最高的粒子作为状态判断依据。为了提高准确程度，就需要更多的粒子以确保粒子可以覆盖到状态空间的更多、更精细的可能。
   而重采样过程是基于达尔文适者生存（survival of the fittest）思想的概率实现：它将粒子集重新聚集在状态空间中具有高后验概率的区域。这样就将滤波算法的计算资源集中在状态空间最重要的区域。

9. 常见的重采样方法有两种：
   1). 直接重采样（Resampling with Replacement）：根据粒子的权重进行有放回的抽样。每个粒子的抽样概率与其权重成正比，权重越高的粒子被选中的概率越大。
   这种方法会产生重复的粒子，即同一个粒子在新的粒子集中出现多次。
   2). 系统重采样（Systematic Resampling）：使用均匀分布来选择粒子，以保证重采样过程中的多样性。首先，根据粒子的权重计算累积概率分布，然后使用一个均匀分布的随机数作为起始点，以固定的步长选择粒子。
   这种方法不会产生重复的粒子，同时保持了原始粒子的分布。
   通常情况下，我们使用系统重采样，其具体实现方式，见实例里的操作。

6.2 实例：简单的粒子滤波定位问题

粒子滤波广泛的应用于目标跟踪，比较出名的算法有，追踪问题上的 Rob Hess 算法、定位问题上的 amcl 算法。
参考《概率机器人》第八章第三节：蒙特卡洛定位

1. 二维地图场景，100*100大小，以x、y、θ描述位置和方向。
2. 粒子在地图中做随机移动，状态转移模型为高斯分布: x’ = x + noise_x, y’ = y + noise_y, θ’ = θ + noise_θ
3. 地图的顶点位置设置三个地标，当做观测。我们可以观测到路标
4. 权重更新方式。参考的是距离和方向：√(∆x^2 + ∆y^2)、∆θ
   这里我们认为我们可以观测到路标，并直接通过当前实际位置生成观测值。而在其它情况下，实际上观测值会带有误差和噪声。
   根据路标点和粒子位置，计算粒子预期的距离和方向。

6.3 手动的求解过程：

略……
看代码注释吧。

6.4 matlab代码验证：

mapSize = 100;

% 初始的真实位置，在地图中央
realPose = [50, 50, 0]; % x, y, θ

% 粒子数
N = 1000;

% 初始化粒子，rand(N, M)表示生成N*M矩阵大小的0-1随机数
% 这里rand(N, 1) * mapSize，表示散布在地图里粒子的 x 或 y 坐标（取值范围0~100）
% rand(N, 1) * 2 * pi，表示散布在地图里粒子的角度 θ（取值范围-pi~pi）
particles = [rand(N, 1) * mapSize, rand(N, 1) * mapSize, rand(N, 1) * 2 * pi - pi]; % x, y, θ
plot(particles(:, 1), particles(:, 2), 'r.');
pause(1);

% 地标（特征）位置，在地图的顶点位置设置三个地标
landmarks = [0, 0; mapSize, 0; mapSize, mapSize];

% 进行50次迭代
for t = 1:50
    % 实现粒子滤波第一步：构建一个假想的粒子集
    % 真实位置随机移动,粒子也随机移动
    realPose = realPose + [randn(1, 1), randn(1, 1), rand * 2 * pi - pi];
    particles = particles + [randn(N, 1), randn(N, 1), rand(N, 1) * 2 * pi - pi];

    % 粒子滤波第二步：状态转移概率中采样得到预测粒子集。
    % 此步在这里可以被省略
    % 若操作该步骤，可以参考以下
    % 假设状态转移模型为高斯分布: x' = x + noise_x, y' = y + noise_y, θ' = θ + noise_θ
    noise_x = randn(N, 1);
    noise_y = randn(N, 1);
    noise_theta = randn(N, 1);
    % 根据状态转移模型，采样预测粒子集
    particles = particles + [noise_x, noise_y, noise_theta];


    % 实现粒子滤波第三步：重要因子、也就是粒子的权重计算
    % 初始化权重参数，其维度与粒子数量一样，每个维度对应一个粒子的后验
    weights = zeros(N, 1);

    % 残差计算
    for i = 1:size(landmarks, 1)
        % 计算得到测量距离和方向
        % 这里我们认为我们可以观测到路标，并直接通过当前实际位置生成观测值。（实际上观测值会带有误差和噪声）
        realRangeBearings = [sqrt(sum((landmarks(i, :) - realPose(1:2)).^2, 2)), ...    % √(∆x^2 + ∆y^2)
                            atan2(landmarks(i, 2) - realPose(2), landmarks(i, 1) - realPose(1)) - realPose(3)]; % ∆θ
        % 根据测量得到的位置和方向，计算粒子预期的距离和方向
        particleRangeBearings = [sqrt(sum((particles(:, 1:2) - repmat(landmarks(i, :), N, 1)).^2, 2)), ...
                                atan2(landmarks(i, 2) - particles(:, 2), landmarks(i, 1) - particles(:, 1)) - particles(:, 3)];
        % 根据测量的距离和方向以及预期的距离和方向，计算粒子的权重。有三个路标，所以这里是累加
        % exp(n): e的n次方(指数函数)。
        % .^2: 矩阵中的每个元素都求平方。
        % sum(a, 2): 矩阵按行求和，输出一个列向量。sum(a, 2):矩阵按列求和。
        weights = weights + exp(-0.5 * sum((particleRangeBearings - realRangeBearings).^2, 2));
    end
    % 归一化权重
    weights = weights / sum(weights);


    % 实现粒子滤波第四步：根据权重重采样
    % indices = randsample(1:N, N, true, weights); 
    % 以下是手动实现系统重采样参考
    % 计算累积权重,按列顺序进行累积计算
    cumulativeWeights = cumsum(weights);
    % 生成 N 个随机数，范围为 [0, 1)
    randNums = rand(N, 1);
    % 初始化索引向量
    indices = zeros(N, 1);
    % 进行系统重采样
    for i = 1:N
        % 根据随机数值找到对应的粒子索引
        % find(x,n）函数默认查询非零元素的位置，即对x矩阵查询前n个非零元素的位置
        % 以下表示在 cumulativeWeights 数组中查找第一个大于等于 randNums(i) 的元素，并返回其索引。
        index = find(cumulativeWeights >= randNums(i), 1);
        indices(i) = index;
    end
    % 得到回归后验分布的粒子集
    particles = particles(indices, :);


    % 画出粒子和真实位置
    plot(particles(:, 1), particles(:, 2), 'r.');
    hold on;
    plot(realPose(1), realPose(2), 'b*');
    plot(landmarks(:,1), landmarks(:,2), 'go', 'MarkerSize',10, 'LineWidth', 2);
    hold off;
    axis([0 mapSize 0 mapSize]);
    drawnow;
    % 为方便观察，每次显示延迟0.5s
    pause(0.5);
end

6.5 结果分析：

通过matlab得到的结果为：


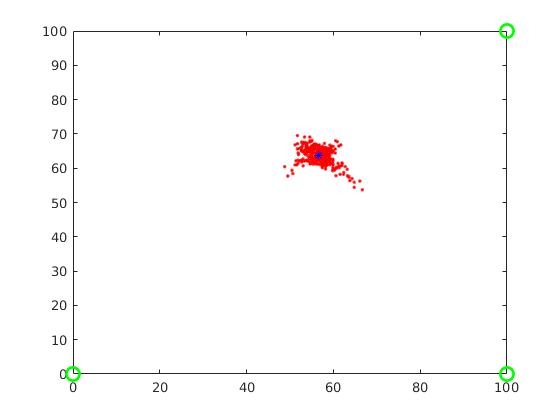
可以看到粒子集逐渐收敛到了真实位置附近。

over~

十月