前言

本文教程均来自b站【小白也能听懂的人工智能原理】，感兴趣的可自行到b站观看。

本文【原文】章节来自课程的对白，由于缺少图片可能无法理解，故放到了最后，建议直接看代码（代码放到了前面）。

代码实现

dataset.py内容如下

import numpy as np

def get_beans(counts):
	xs = np.random.rand(counts)
	xs = np.sort(xs)
	ys = [1.2*x+np.random.rand()/10 for x in xs]
	return xs,ys

Rosenblatt感知器代码如下

import utils.dataset as dataset
from matplotlib import pyplot as plt

## Create a dataset
n=100
xs,ys=dataset.get_beans(n)
plt.title('Size-Toxicity Function',fontsize=12)
plt.xlabel('Bean Size',fontsize=12)
plt.ylabel('Toxicity')
plt.scatter(xs,ys)


## Roseblatt
w=0.5
alpha=0.05
for _ in range(100):
    for i in range(n):
        x=xs[i]
        y=ys[i]
        y_pre=w*x
        e=y-y_pre
        w=w+alpha*e*xs

## Visualization
y_pre=w*xs
plt.scatter(xs,ys)
plt.plot(xs,y_pre,'r')
plt.show()

实验结果

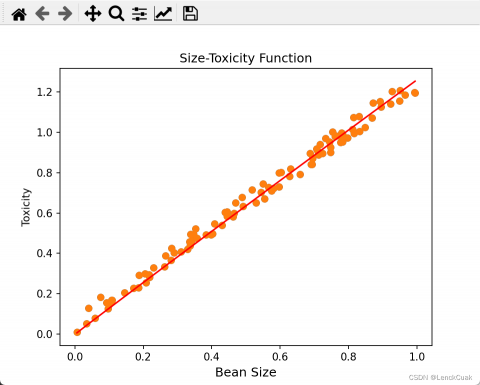
原文

有人说我们是上帝的作品，也有人说我们自己就是上帝，但我认为把人作为中心讨论却大可不必，因为地球上有那么多的生物，智能又何必是人，不如让我们看看那些更加原始和简单的生物遇到的问题和它们具有的智能。

在很深很深很深的海底住着一个简简单单的生物小蓝，他的世界很简单，去寻找周围能够吃到了一种叫做豆豆的植物，并靠此生存。但是这些豆豆在漫长的演化历史中，通过和小蓝的反复博弈，为了保护自己逐渐进化出了毒性，毒性的强弱和豆豆的大小有关系，而小蓝也进化出了一个能够检测豆豆大小的器官，那么问题来了，小蓝如何根据豆豆的大小判断它到底有多毒呢？​

没错，它还缺一个思考的器官，也就是我们常说的脑子，但我们又如何去描述思考或者说认知？**认知以前当然就是一无所知，这种情况下认知事物唯一的方法就是依靠直觉。那我们又该如何去描述直觉呢？很明显是函数。**为什么是函数？仔细想想，我们本来一直就在用函数认识这个世界，在物理中一个质量为m的物体，在不同的受力f下产生加速度a，这是一个以f为自变量，m为产生a为因变量的函数。在经济学中我们把消费投资、政府购买和进出口作为自变量，也可以形成一个关于GDP的函数。

实际上除了这些严格的领域，在很多不那么严格的事情上，如果你愿意，其实也可以用函数去描述认知，比如气温对人心情的影响可能是这样的一个函数，一只小狗的眼睛大小和它可爱程度的关系，可能是这样的一个函数，而后者这种不严格人类更加擅长的问题，也就是我们人工智能要解决的问题，找到一个恰当的函数去描述它。

如此这般把智能体对世界认知的过程看作是在脑中不断形成各种函数，似乎也就好有道理，既然是直觉，那么就不需要太多的理由，豆豆的毒性和它的大小有关系，所以这里的直觉自然是一个一元一次函数，豆豆的大小x是自变量，毒性y是因变量，而w是一个确定的参数。就是我们常说的直线的斜率，一个简单的一元一次函数就可以描述一个直觉，建立一种思考的模型。当我们去类比生物神经元的时候，你就会发现用一个一元一次函数去描述认知，可不是乱用的，完全是有备而来。

这实际上就是早在1943年由神经学家McCulloch和数学家Pitts在他们合作的论文中提出了一种神经元模型，McCulloch-Pitts模型。这个模型是对生物神经元一种相当简化的模仿，通过树突进入神经元，再通过轴突输出结果，它们分别对应着函数中的自变量和因变量输出，一般来说有很多个输入端，如果只有一个输入，也就是一元函数。如果是两个，那就是二元函数，比如豆豆的毒性不仅和它的大小有关，也和颜色有关，三个输入就是三元函数等等。而至于参数w它实际上起着控制输出上输入信号的作用，换句话说控制着不同输入对输出的影响，我们也称之为权值。因为我们在判断一个东西的时候，不同因素对结果的重要性都不太一样，也正因为如此，我们会发现McCulloch-Pitts选择用一次函数，而不是其他函数来模仿神经元是一件很自然的事情，树突输入x被权值参数w扩大或缩小，然后轴突输出简单且有效。

当然完整的 McCulloch-Pitts 模型中还有一个偏置项b而在一次函数后还会加上一个激活函数用来激活行进元的输出，我们会在后面讨论这些东西，简单起见暂且不表，还是回到这个树突，只有一个输入端的神经元上面来，为了理解方便，我们用简化的图形来表示，那么小蓝靠这个神经元可以存活下去吗？看得出来随着w取不同的值，这个值距函数往往会产生很多的错误，当然也不排除小蓝的直觉很准，就像这样，那么我们现在面临的问题就是这个一元一次直线函数中的参数w设置为多少，小蓝才能很好的进行预测。

也就是说如何从偏离现实的直觉过渡到符合现实的认知，比如小蓝，大脑中神经元的权重值w一开始是0.1，看见一个大小为0.59的豆豆，经过神经元的计算认为毒性是0.059，于是一口吃进去。糟糕，其实它的毒性是0.68，具有极高的毒性，很明显小蓝现在的神经元很草率，作为早已具有智能的人类，我们知道把w调大一点再大一点这样就好了。但是机器又怎么知道呢？

最开始McCulloch-Pitts模型中的权重值确实需要手工调整，并没有自动的学习方法，这未免有点太不智能了，于是在1958年一名叫做Rosenblatt​的心理学家在麦卡罗和皮斯模型上指出了，Rosenblatt​感知器模型，他让神经元有了自己调整参数的能力。​

Rosenblatt感知器是第一个从算法上完整描述的神经元，在此之后受到他的启发，工程界、物理学界、数学界就开始纷纷投入神经网络的研究，人工智能也开始了蓬勃的发展。我们来看一下Rosenblatt感知器是怎么做到让神经元能够改的。当然本着“如无必要，勿增新知”的理念，我们还是考虑只有一个输入的情况，其实很简单也很直观，输入通过McCulloch-Pitts神经元模型之后输出一个结果，用标准答案减去这个结果，这意味着预测和标准之间的误差，然后自然是根据这个误差去调整参数。

比如我们让w直接加上这个误差，再让结果作为新的w。看这样就做到了，预测过小的时候误差为正数，w加上误差之后向大调整，下次预测的时候结果就提升了，反过来当预测过大误差是负数的时候，w向小调整。

这就是罗森布拉特感知器的学习过程，通过误差修正参数。当然在Rosenblatt感知器模型中误差还有乘以输入x，这是为何呢？我们知道豆豆的大小只能是一个正值，小于0的豆豆，可谓让人匪夷所思，但是以后我们一定会遇到输入值是负数的情况，当输入数据是负数的时候，你会发现事情正好相反，预测过大的时候需要增加w而不是减少，而预测过小的时候需要减小w而不是增加。​​

所以我们让输入x乘以误差，事情就被巧妙的解决了：当x为正数的时候预测过大，误差为负数乘以x之后还是负数，w减小；预测过小，误差为正数乘以x之后还是正数，w增大；而当x为负数的时候，预测过大误差为负数乘以x之后变成正数，w增大，预测过小误差为正数乘以x之后变为负数，w减小。

当然误差除了乘以输入x之外，Rosenblatt感知器模型还让误差乘以了一个系数alpha，比如0.05，这意味着我们每次修正的时候幅度都降低了20倍，这个alpha也就是所谓的学习率，这又是为何呢根据奥卡姆的剃刀原理，我们不妨先拿掉这个学习率参数，看看会怎么样？

这时候参数调整的过程是这样子，不对劲，我们让阿尔法等于0.5，是这样的。还是不对劲，我们这样阿尔法等于0.1，是这样的。唉我们好像发现问题了，事实上阿尔法等于0.0935。好像卡bug了，当我们继续把阿尔法向小调整，我们终于发现参数调整的过程震荡越来越小。没错，让误差乘以学习率是为了防止调整幅度过大，错过最佳点，就好像一个人如果他每走一步得出固定的一米，而他一开始在距离远点0.5米的位置，那么不论他怎样都到达不了原点，当然学习率也不是越小越好，太小的学习率会让这个调整的过程磨磨唧唧让人心酸了。

这就是Rosenblatt感知器的全部工作原理了。

当然机器学习的本质是数学，一切设计必须有数学的支撑，比如这里通过误差修正参数，误差还乘以了输入和学习率，这个看起来就很玄乎的公式，虽然直观上很符合我们的感受，但是又能保证客观上通过这种方式就一定能够调整出一个合适的参数，而不是越来越远离正确值，也就是说如何从数学上证明这个模型中的w调整方法最后就一地收敛了。Rosenblatt感知器之所以拥有如此重要的历史地位，就像我们说的那样，他第一次完整的从算法上描述了一个神经元，这种描述当然也包括数学证明，但这个感知器收敛定理的证明过程有点冗长且繁琐，我们就不逐个解释了，有兴趣的同学可以自行推导，当然证明的事情只是一颗定心丸而已，让我们相信他在数学上是合理的，如果同学们去证明有困难，也不会影响后续内容的理解。

你只要相信这个感知器模型在数据上确实可以被证明w一定会收敛于某个值。在现代机器学习神经网络应用中，古老的Rosenblatt感知器的学习方法已经很少采用。接下来我们将看到一种目前比较常用的学习方式梯度下降和反向传播。