参考《数值最优化方法》、知乎专栏：https://www.zhihu.com/column/numerical-optimization

一、梯度（gradient）向量、雅克比（Jacobian）矩阵、海森（Hessian）矩阵

1.1 梯度（gradient）向量

目标函数f为单变量，是关于自变量x=(x1,x2,…,xn)T的函数，单变量函数f对向量x求梯度，结果为一个与向量x同维度的向量，称之为梯度向量。
梯度向量的方向是函数在该点上升最快的方向，其模长表示函数在该点的变化率。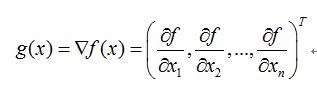

例如：

1.2 雅克比（Jacobian）矩阵

目标函数f为多变量f=(y1,y2,…,ym)T，是关于自变量x=(x1,x2,…,xn)T的函数，雅可比矩阵描述了函数每个输出分量对于每个输入分量的偏导数。
雅克比矩阵与梯度向量的区别就是，雅克矩阵比目标函数f为多变量 而 梯度向量目标函数f为单变量。目标函数f为单变量的情况下，雅克比矩阵就是梯度向量。
函数如下表达：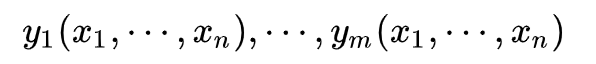

则其雅克比矩阵为：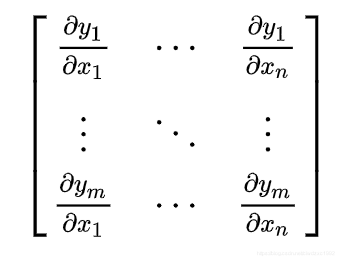

例如：

1.3 海森（Hessian）矩阵

目标函数f为多变量f=(y1,y2,…,ym)T，是关于自变量x=(x1,x2,…,xn)T的函数，雅可比矩阵描述了函数每个输出分量对于每个输入分量的二阶偏导数。
故，海森矩阵要求所有二阶导数都存在。
海森矩阵的特征值和特征向量可以提供函数在某一点的曲率和最速下降方向。
函数如下表达：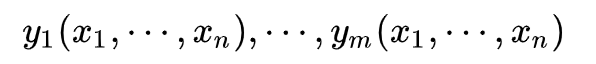

则其海森矩阵为：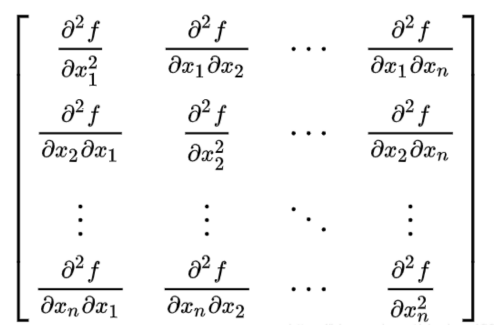

例如：

1.4 关于泰勒展开

雅克比矩阵和海森矩阵的真正意义是用来近似损失函数。
近似的方式就是泰勒展开。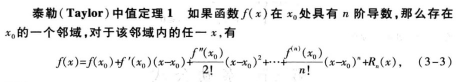

后面我们所说的一阶、二阶的意思就是，保留损失函数泰勒展开的一阶、二阶项去近似损失函数。
当然，这个世界远不止二阶这么简单……但我们通过传统方式也就算到这里了。
神经网络在某种程度上可以被视为一种高阶的函数逼近方法，与最优化方式很像。

二、最优性条件与算法

2.1 局部最优性条件

如上图，A 为局部极大值点；B 为局部极小值点；C 为全局极大值点；D 为全局极小值点。
在一般优化算法里，我们所讨论的都是局部最优解，尤其是局部极小值点的性质。
这里，符号约束， Θ 为参数变量； f(Θ) 为函数值； J(Θ) 为一阶导函数值，又叫一阶梯度值； H(Θ) 为二阶导函数值，又叫二阶梯度值；要寻找的局部最优点用 Θ* 表示。

1. 定理1：若 f(Θ) 存在一阶导，Θ_ 为 f(Θ) 一个局部极小点，则 J(Θ_)=0
   f(Θ) 局部极小点 的 一阶必要条件。
   连续不一定可导,可导一定连续……

2. 定理2：若 f(Θ) 存在二阶导，Θ_ 为 f(Θ) 一个局部极小点，则 H(Θ_) 半正定
   f(Θ) 局部极小点 的 二阶必要条件。
   设M是n阶方阵，如果对任何非零向量 z，都有 (zT)Mz> 0，其中 zT 表示 z 的转置，就称 M 为正定矩阵。
   若 >=0，则称为半正定。

3. 定理3：若 f(Θ) 存在二阶导，在 Θ_ 处有 J(Θ_)=0，则 H(Θ_) 正定时，则 Θ_ 是 f(Θ) 的严格局部极小值点
   f(x) 局部极小点 的 二阶充分条件。

4. 定理4：若 f(Θ) 存在一阶导，则 f(Θ) 在点 Θ 处沿方向 d （d!=0）的一阶方向导数可以表示为 图一 所示；若 f(Θ) 存在二阶导，则 f(Θ) 在点 Θ 处沿方向 d （d!=0）的二阶方向导数可以表示为 图二 所示
   f(Θ) 的 一、二阶方向导数的计算。
   图一：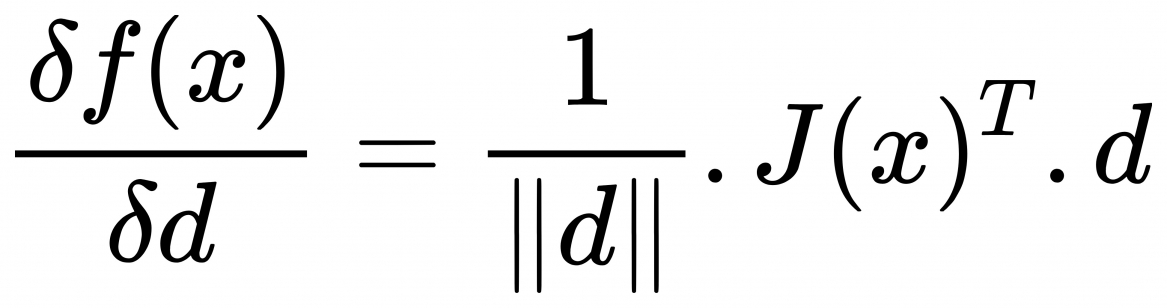
   
   图二：
   

5. 定理5：若 f(Θ) 存在一阶导，Θ_ 为 f(Θ) 一个局部极小点，则 f(Θ) 在 Θ_ 处沿任意方向的一阶方向导数为零
   f(Θ) 局部极小点 的 一阶必要条件。

6. 定理5：若 f(Θ) 存在二阶导，f(Θ) 在 Θ_ 处沿任意方向的一阶方向导数 为零，则当 f(Θ) 在点 Θ_ 处沿任意方向的二阶方向导数为正时，Θ* 是 f(Θ) 的严格局部极小值点
   f(Θ) 局部极小点 的 二阶充分条件。

2.2 优化方法

想象一个爬山的场景：首先我们需要选择一个出发点；然后向着山顶的方向一段一段地前进，其中在每一个转折点，我们要选择一个上山的方向，并根据山势选取在这一个方向前进的距离，去到下一个点，这样子依次进行，直至我们认为已经到达山顶。

这是一个极大值的例子，但极小值寻找也是同样的意思，我们有三步：确定方向、确定步长、确定是否终止。（这里的方向、步长都指的是自变量的方向、步长）
解决此类问题的算法被称为无约束最优化算法，算法的执行结构为：

1. 给定初始参数（初始点） Θ ，开始执行；
2. 若在 Θ(k) 处满足终止条件（收敛），则停止迭代、输出结果；终止条件一般与损失函数有关，我们实际就是找损失函数的局部最小值。
3. 确定 f(Θ(k)) 在 Θ(k) 处的下降方向（梯度） d(k)；
4. 确定步长 α(k) ，使得 f(Θ(k) + α(k).d(k)) 较之 f(Θ(k)) 有某种意义的下降，这里的 d(k) 为f(Θ(k))的梯度、α(k) 为 Θ(k) 变化的步长；
5. 令 Θ(k+1)=Θ(k)+α(k).d(k)，k++，转第2步。
6. 注意，为了表示的方便，我们常常会把 f(Θ(k))、 J(Θ(k))、 H(Θ(k)) 写成 f(k)、 J(k)、 H(k)，但需要切记，其自变量是 Θ 而不是 k

可以看到的是，构成一个最优化方法的基本要素有二：其一是下降的方向；其二是步长。也就是说，不同的方法可得到不同的下降方向和步长。在最优化方法中，下降的方向和步长的选取顺序不同，导致产生不同类型的方法。
线搜索方法是在 Θ(k) 处求得下降方向 d(k)，再沿 d(k) 确定步长 α(k)
信赖域方法是先限定步长的范围，再同时确定下降方向 d(k) 和步长 α(k)

平时我们使用的大多是线搜索方法，关于更详细介绍，可以看《数值最优化方法》里的内容，以后再论，这里不做更多介绍了。

2.3 终止准则

算法的另一个重要问题是迭代的终止条件。
一般情况下，我们使用梯度判断来作为终止准则：||J(Θ)|| < ε （ε为一个常数需要设置）
但是这个终止准则也有一定的局限，比如：在极小点邻域比较陡峭的函数，即使该邻域中的点已经相当接近极小点，但是其梯度值可能仍然比较大，从而使迭代难以停止。针对这种情况，我们的解决方法是设置一个最大迭代次数。

其它终止准则有： ||Θ(k) - Θ(k+1)|| < ε 或者 f(Θ(k)) - f(Θ(k+1)) < ε
但只能说明算法此时所进行的迭代对迭代点或迭代点处目标函数值的改善已经很小，并不能保证足够小，并不能充分表明处于极小点处，所以基本上不怎么用这种判断方式。

2.4 收敛性与收敛速度

对一个算法而言，其收敛性是首要问题，在此基础上，算法收敛速度的快慢也是评判一个算法优劣的重要标准。
收敛性的判断：

收敛速度分 线性收敛、超线性收敛、二阶收敛 三种情形。

最速下降法、牛顿法和拟牛顿法都能收敛，收敛速度分别是线性、二次、超线性。
更具体的论证参考：https://zhuanlan.zhihu.com/p/92768338

2.5 二次终止性

对于一个算法，如果它对任意正定二次函数，从任意初始点出发，可以经有限步迭代求得极小点，我们就说该算法具有二次终止性。
梯度下降法、牛顿法、拟牛顿法都具有这个性质，具体论证可以在网上查找，这里不做深入讨论。

三、一阶梯度：梯度下降法（Gradient Descent）

通过对损失函数进行一阶泰勒展开近似，并最小化损失函数。
所以被称为一阶梯度法。

3.1 算法介绍

梯度下降法（Gradient Descent）是优化算法中的一种基本方法，也被称为一阶梯度法，因为它只使用了函数的一阶导数（梯度）来进行参数优化。
它用于最小化一个损失函数（或成本函数），使其收敛到局部最优点或全局最优点。在梯度下降法中，每次更新参数都依赖于损失函数关于参数的梯度（即损失函数对参数的偏导数）。
他的直观意义很明显，只要按照梯度的反方向前进即可。

梯度下降法的基本步骤：

1. 定义损失函数：首先，我们需要定义一个损失函数，它度量模型预测与实际观测之间的差异。在优化问题中，我们希望最小化损失函数。一般损失函数被定义为误差的平方或最小二乘形式。
2. 初始化参数和学习率：初始化要优化的参数Θ(0)，初始化学习率 α(0)。
3. 根据损失函数的梯度计算 d(k)：计算损失函数关于参数的梯度 J(k)（Jacobian矩阵），并计算 d(k) = -J(Θ(k)) ，其告诉我们损失函数在当前参数值处的变化方向和速率。
4. 一维精确线搜索求学习率 α(k)（关于这一步以后再做详细讨论，目前就固定一个常值做学习率）。
5. 更新参数：通过沿着梯度方向调整参数值来更新参数：Θ(k+1) = Θ(k) + α(k).d(k)。这样做可以使损失函数逐渐减小。
6. 重复迭代：重复步骤3和步骤4，直到满足停止条件（例如达到一定的迭代次数或梯度变化足够小）。
7. 注意，为了表示的方便，我们常常会把 f(Θ(k))、 J(Θ(k))、 H(Θ(k)) 写成 f(k)、 J(k)、 H(k)，但需要切记，其自变量是 Θ 而不是 k

优点：

1. 简单易实现：梯度下降法相对于其他复杂的优化算法来说较为简单，易于实现和理解，是最常用的优化算法之一，被广泛应用于各种问题；
2. 收敛性：梯度下降法通常在适当的学习率下能够收敛到局部最优解，特别是在目标函数是凸函数的情况下，可以保证收敛到全局最优解；
3. 内存效率：相比于牛顿法等需要计算海森矩阵的优化算法，梯度下降法只需要存储目标函数的一阶导数（梯度），因此在内存使用上较为高效。

不足：

1. 收敛速度慢：梯度下降法通常具有较慢的收敛速度，特别是在目标函数具有复杂非线性特性的情况下，可能需要较多的迭代步骤才能收敛到最优解；
2. 依赖学习率：梯度下降法的收敛性和稳定性很大程度上依赖于学习率的选择。学习率太小会导致收敛速度缓慢，学习率太大可能导致发散；
3. 容易陷入局部最优解：梯度下降法只能保证收敛到局部最优解，对于非凸函数的情况，可能会陷入局部最优解而无法找到全局最优解。

关于梯度下降法的学习率：
在一阶梯度法中，学习率乘以梯度给出了下一步的步长和方向。梯度决定了应该往哪个方向移动，学习率决定了移动的步长。因此，梯度指示了移动的方向，学习率决定了步长。

1. 初始尝试： 通常可以从一个较小的学习率开始尝试，例如 0.1 或更小。这可以帮助确保算法在开始时不会跳过最优解。
2. 学习率调整： 如果发现算法收敛速度过慢，可以逐步增加学习率。然而，过大的学习率可能导致算法不稳定甚至发散。
3. 学习率衰减： 一种常用的策略是使用学习率衰减，即在训练的每个阶段逐渐减小学习率。这有助于在初始阶段更快地收敛，而后期可以更稳定地靠近最优解。
4. 自适应学习率方法： 还有许多自适应学习率方法，如 AdaGrad、RMSprop 和 Adam 等，它们会根据参数的历史梯度信息自动调整学习率，通常更能适应不同问题。
5. 交叉验证： 在实际应用中，可以尝试不同的学习率值，并使用交叉验证来选择效果最好的学习率。

关于损失函数的定义：
一般损失函数代表拟合值与真值之间的差值，并且取绝对值。
但是绝对值不方便求导，故一般定义为差值的平方。
有的地方会取对数什么的。
比较著名的是最小二乘问题，这个问题在这篇博客里还用不上，后续的高斯牛顿、LM算法都基于非线性最小二乘问题。
本文实例的损失函数都为拟合值与真值之间的差值的平方。

3.2 代码实例

注意不同的学习率、初值、损失函数对曲线拟合的结果影响较大。

clear;clc;

%% 真实值
a = 0.5;
b = -0.5;
c = 1.0;
% 横坐标取值：1-100每隔两个数取一个数，并除以100
x = (1:2:100)./100; 
% 产生待拟合数据 
nosie = 0.005*randn(1,size(x,2)); % size(x,1) 指矩阵的行数；size(x,2) 就是矩阵的列数；
y = a*x.^2 + b*x + c + nosie;
% 显示
% scatter(x,y,100,'black','.');


%% 梯度下降法（Gradient Descent）、一阶梯度法
% step0:定义最大迭代次数
max_iter = 10000;

% step1:定义损失函数，初始化loss值
loss_function = @(val) mean((val(1) * x.^2 + val(2) * x + val(3)) - y).^2;
loss = zeros(1, max_iter);

% step2:定义雅克比矩阵（一阶梯度、一阶偏导数）
Jacobian_function = @(val) [mean(2 * x.^2 .* (val(1) * x.^2 + val(2) * x + val(3) - y)); % 返回一个列向量（与优化参数theta对应）
                            mean(2 * x .* (val(1) * x.^2 + val(2)* x + val(3) - y));
                            mean(2 * (val(1) * x.^2 + val(2) * x + val(3) - y))];

% step3:初始化参数（theta）、学习率（alpha）、收敛容差（epsilon）
alpha = 0.25;
theta = [0.35; -0.25; 1.5]; % 列向量
epsilon = 1e-5;

% 使用梯度下降法拟合
for iter = 1:max_iter
    % step4:计算梯度
    gradient = Jacobian_function(theta);

    % step5:更新系数
    delta = -gradient;
    theta = theta + alpha * delta;

    % step6:计算损失函数的值
    loss(iter) = loss_function(theta);

    % step7:根据损失函数值以及迭代次数判断是否退出拟合
    if norm(Jacobian_function(theta)) < epsilon
        fprintf('结束时迭代次数： %d, 结束梯度值： %.8f \n', iter, norm(Jacobian_function(theta)));
        break;
    end
    % ...
end

% 输出拟合的参数
fprintf('拟合的参数：a = %.4f, b = %.4f, c = %.4f\n', theta(1), theta(2), theta(3));


%% 绘制原始数据点和拟合的曲线
figure;
scatter(x, y, 100, 'black', '.');
hold on;
plot(x, (theta(1) * x.^2 + theta(2) * x + theta(3)), 'r', 'LineWidth', 2);
xlabel('X');
ylabel('Y');
title('Gradient Descent: Curve Fitting');
legend(' raw data', ' Fit curve');
grid on;

% 绘制loss变化曲线，这里为了方便观察只看前200个loss数据
figure;
plot(loss(1:200))
axis([-inf, inf,0,0.1])
title('Gradient Descent: Loss');
grid on;

3.3 结果

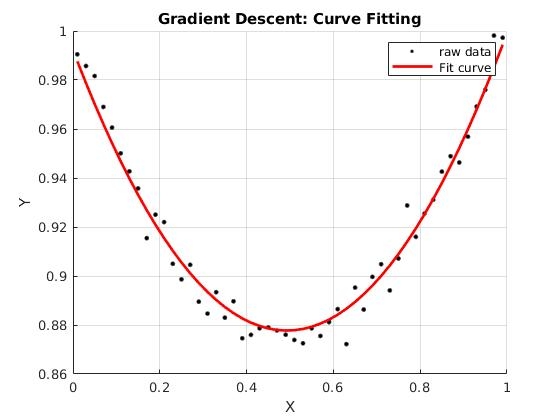
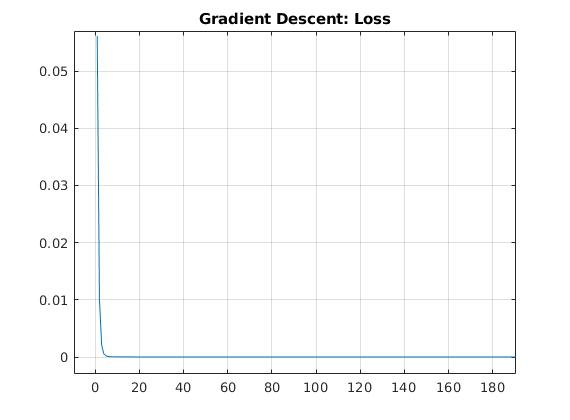
终端打印：

结束时迭代次数： 3584, 结束梯度值： 0.00000999 
拟合的参数：a = 0.5070, b = -0.5054, c = 1.0003

四、二阶梯度：牛顿法（Newton-Raphson）

通过对损失函数进行二阶泰勒展开近似，并最小化损失函数。
所以被称为二阶梯度法。

4.1 算法介绍

牛顿法（Newton-Raphson）是由数学家Isaac Newton提出的，也被称为二阶梯度法，通过使用目标函数的一阶和二阶导数信息来逐步逼近最优解，该方法在目标函数具有二阶连续导数的情况下收敛较快。

牛顿法的基本步骤：

1. 定义损失函数：首先，我们需要定义一个损失函数，它度量模型预测与实际观测之间的差异。在优化问题中，我们希望最小化损失函数。一般损失函数被定义为误差的平方或最小二乘形式。
2. 初始化参数：选择初始参数作为优化的起始点。
3. 根据计算损失函数的Jacobian矩阵和Hessian矩阵计算 d(k) ： d(k) = -inv(G(K)) * J(K)。梯度（Jacobian矩阵）告诉我们损失函数在当前参数点的变化方向和速率，而Hessian矩阵提供了更多关于目标函数曲率的信息。这一步是牛顿法与梯度下降法的主要区别，牛顿法使用了二阶导数信息，可以更快地收敛到最优解。
4. 更新参数：Θ(k+1) = Θ(k) + d(k)。
5. 重复迭代：重复步骤3和步骤4，直到满足停止条件（例如达到一定的迭代次数或梯度变化足够小）。
6. 注意，为了表示的方便，我们常常会把 f(Θ(k))、 J(Θ(k))、 H(Θ(k)) 写成 f(k)、 J(k)、 H(k)，但需要切记，其自变量是 Θ 而不是 k

优点：

1. 收敛速度快：牛顿法通常具有较快的收敛速度，特别是在目标函数局部具有良好的二次收敛性的情况下。它能够更快地逼近最优解，尤其对于复杂的非线性问题效果显著；
2. 更精确的逼近：相比梯度下降法等一阶优化算法，牛顿法利用目标函数的局部二次近似来进行参数更新，因此更能精确地逼近最优解；
3. 鲁棒性：在目标函数局部具有二次收敛性的情况下，牛顿法通常表现较稳健，能够较好地收敛到最优解。

不足：

1. 计算复杂度高：牛顿法需要计算目标函数的一阶导数（梯度）和二阶导数（海森矩阵），特别是在参数较多的情况下，计算海森矩阵的代价较高，导致计算复杂度增加。
2. 对初始点敏感：牛顿法对于初始参数的选择较为敏感，不同的初始点可能会导致不同的收敛结果，甚至可能发散。在应用中，需要进行仔细的初始点选择或采取一些初始化策略来提高稳定性。
3. 需要海森矩阵可逆：牛顿法需要计算海森矩阵的逆，因此海森矩阵必须是可逆的。在某些情况下，海森矩阵可能不可逆，导致无法应用牛顿法。
4. 受海森矩阵正定的影响：为确保快速收敛到局部最小，需要海森矩阵正定。下面会详细介绍其影响。

关于牛顿法的学习率和损失函数：
在牛顿法里，梯度（雅克比矩阵）与一阶梯度法里一样，依旧用来确定移动的方向。
但可以发现，牛顿法里我们并没有确定学习率，而是使用Hessian矩阵的逆来调整步长，注意是使用Hessian矩阵的逆来调整步长，而不是直接代替学习率确定步长。
在一阶梯度里，学习率决定步长、梯度决定方向；而在牛顿法里，不需要设置学习率这个参数，步长在迭代公式中通过 Hessian 矩阵的逆和梯度计算得到。
这种步长调整方式是牛顿法的独特特点，它利用了 Hessian 矩阵的信息来决定每次迭代的步长，从而更精确地逼近极小值点。
在牛顿法里，我们希望通过考虑二阶信息（Hessian矩阵）来调整步长，以便更智能的确定步长。
损失函数的定义与一阶梯度法一样，这里设置为误差的平方。

关于海森矩阵是否正定，对牛顿法的影响：

1. 如果海森矩阵是正定的，即所有特征值都大于零，那么牛顿法通常能够快速收敛到局部最小值。正定海森矩阵保证了损失函数在当前点附近是凸函数，因此牛顿法的迭代方向是下降最快的方向，能够快速趋近最优解；
2. 如果海森矩阵不是正定的，部分特征值为正，部分为负，这可能导致牛顿法在某些方向上朝着局部最小值迭代，而在其他方向上朝着局部最大值或鞍点迭代，从而导致收敛速度较慢或陷入局部最大值；
3. 如果海森矩阵不是正定的，存在零特征值，这可能导致牛顿法在某些方向上无法判断应该朝着何方迭代，从而导致收敛困难或失败；
4. 为了应对海森矩阵非正定的情况，进行正定性修正：在海森矩阵中加入正定修正项，使其变为正定。这可以通过加入单位矩阵的某个倍数来实现，从而确保海森矩阵的正定性，从而改善收敛性。也可以使用近似的海森矩阵实现，比如拟牛顿法就是这么做的。

4.2 代码实例

clear;clc;

%% 真实值
a = 0.5;
b = -0.5;
c = 1.0;
% 横坐标取值：1-100每隔两个数取一个数，并除以100
x = (1:2:100)./100; 
% 产生待拟合数据 
nosie = 0.005*randn(1,size(x,2)); % size(x,1) 指矩阵的行数；size(x,2) 就是矩阵的列数；
y = a*x.^2 + b*x + c + nosie;
% 显示
% scatter(x,y,100,'black','.');


%% 牛顿法（Newton-Raphson）、二阶梯度法
% step0:定义最大迭代次数
max_iter = 100;

% step1:定义损失函数，初始化loss值
loss_function = @(val) mean((val(1) * x.^2 + val(2) * x + val(3)) - y).^2;
loss = zeros(1, max_iter);

% step2:定义雅克比矩阵（一阶梯度）和海森矩阵（二阶梯度）
Jacobian_function = @(val) [mean(2 * x.^2 .* (val(1) * x.^2 + val(2) * x + val(3) - y)); % 返回一个列向量（与优化参数theta对应）
                            mean(2 * x .* (val(1) * x.^2 + val(2)* x + val(3) - y));
                            mean(2 * (val(1) * x.^2 + val(2) * x + val(3) - y))];

hessian_function = @(val) [ mean(2 * x.^4)  mean(2 * x.^3)  mean(2 * x.^2); % 返回一个矩阵（与优化参数theta对应）
                            mean(2 * x.^3)  mean(2 * x.^2)  mean(2 * x);
                            mean(2 * x.^2)  mean(2 * x)     2];

% step3:初始化参数（theta）、收敛容差（epsilon）
theta = [0.35; -0.25; 1.5]; % 列向量
epsilon = 1e-5;

% 使用牛顿法进行优化
for iter = 1:max_iter
    % step4:计算梯度和Hessian矩阵
    gradient = Jacobian_function(theta);
    hessian = hessian_function(theta);

    % step5:更新参数
    delta = - hessian\gradient; % inv(hessian) * gradient;
    theta = theta + delta;

    % step6:计算损失函数的值
    loss(iter) = loss_function(theta);

    % step7:根据损失函数值以及迭代次数判断是否退出拟合
    if norm(Jacobian_function(theta)) < epsilon
        fprintf('结束时迭代次数： %d, 结束梯度值： %.8f \n', iter, norm(Jacobian_function(theta)));
        break;
    end
    % ...
end

% 输出拟合的参数和损失函数的值
fprintf('拟合的参数：a = %.4f, b = %.4f, c = %.4f\n', theta(1), theta(2), theta(3));


%% 绘制原始数据点和拟合的曲线
figure;
scatter(x, y, 100, 'black', '.');
hold on;
plot(x, a * x.^2 + b * x + c, 'r', 'LineWidth', 2);
xlabel('X');
ylabel('Y');
title('Newton-Raphson: Curve Fitting');
legend(' raw data', ' Fit curve');
grid on;

% 绘制loss变化曲线，这里为了方便观察只看前50个loss数据
figure;
plot(loss(1:50));
axis([-inf, inf,0,0.1])
title('Newton-Raphson: Loss');
grid on;

4.3 结果

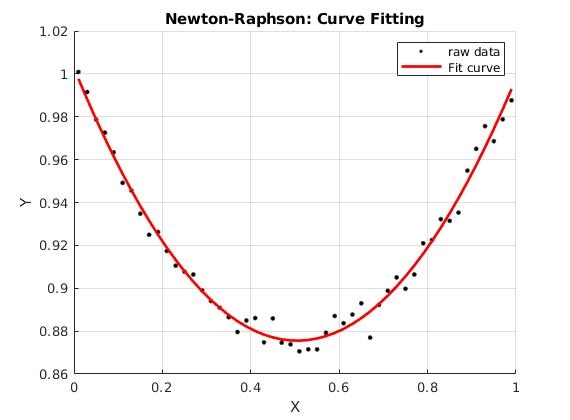
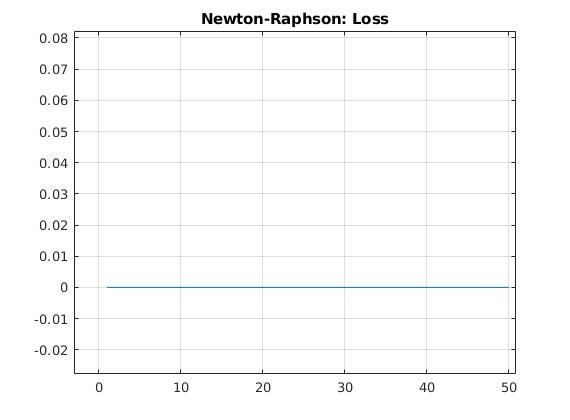
终端打印：

结束时迭代次数： 1, 结束梯度值： 0.00000000 
拟合的参数：a = 0.4955, b = -0.4988, c = 1.0010

可以看到它就迭代了一次达到最好的效果……

over~

本文只针对最优化入门的内容，下一章将介绍二阶梯度法的改进，拟牛顿法，由于拟牛顿法涉及的内容会多些，就不弄到同一篇文章里了。
数值最优化确实难啃，在开始的话，我把一些看不明白、推导复杂的东西暂时跳过了。
这本书不出意外会反复看好几遍，所以，在内容上，不一定完全按照最优化的书里的章节步骤来，仅记录自己的理解过程。
附萌萌的荒天帝~