目录
前言
这个学期学校开设了相应的课程,同时也在学习古月居机器人学系列的《基于栅格地图的机器人路径规划指南》,为了巩固知识,方便自己的学习与整理,遂以学习笔记的形式记录。
1. 轨迹规划
全局路径由一系列路径点构成,这些路径点只要包含空间位置信息即可,也可以包含姿态信息,但是不需要与时间相关,这些路径点被称为全局路径点。
路径(Path)和轨迹(Trajectory)的区别就在于,轨迹还包含了时间信息,轨迹点也是一种路径点,它在路径点的基础上加入了时间约束。
1.1 轨迹规划包括以下几个问题:
- 对工作对象及作业进行描述,给出轨迹上若干个节点;
- 用一条轨迹通过或逼近节点,此轨迹可按一定的原则优化,如加速度平滑得到直角空间的位移时间函数X(t)或关节空间的位移时间函数q(t);
- 在节点之间如何进行插补,即根据轨迹表达式在每一个采样周期实时计算轨迹上点的位姿和各关节变量值;
- 规划机器人的运动轨迹时,需明确其路径上是否存在障碍约束的组合。
- 在空间中进行轨迹规划,需要给定车辆在起始点和终止点的位形;
- 对轨迹进行插值时应满足一系列的约束条件,例如初始点和停止点等关键节点上的位姿、速度和加速度的要求;
- 与此相应的在整个时间间隔内的连续性要求以及其极值必须在车辆性能的容许范围之内等。
满足所要求的约束条件之后,可以选取不同类型的关节插值函数,生成不同的轨迹。常用的关节空间插补有以下方法:
- 三次多项式插值
- 过路径点的三次多项式插值
- 用抛物线过渡的线性插值
- 高阶多项式插值
2. 三次多项式插值
在无人车或机器人机械臂运动过程中,若位置的起始和终止点已知,可以用通过起始点和终止点的一个平滑轨迹函数\(\theta (t)\\)来表示。 为实现系统的平稳运动,轨迹函数\(\theta (t)\\)至少需要满足四个约束条件,即两端点位置约束和两端点速度约束。
端点的位置约束是指起始位姿和终止位姿分别所对应的关节角度。\(\theta (t)\\)在时刻\({t_0}\\)=0时是起始关节角度\({\theta _{\rm{0}}}\\),在终端时刻tf时是终止关节角度\({\theta _f}\\),即
为满足运动速度的连续性要求,起始点和终止点的速度可简单地设定为零。
轨迹规划方法一般是在机器人的初始位置和目标位置之间用多项式函数来“内插”或“逼近”给定的路径,并产生一系列的控制点。若只给出无人车起始点和终止点的关节角度,由于缺少足够的约束,会产生多解,如下图所示。

对于一般的轨迹规划问题,首先列出相应的三次多项式:
\(\theta \left( t \right) = {a_0} + {a_1}t + {a_2}{t^2} + {a_3}{t^3}\\)
再对其分别求一阶导和二阶导,得到速度和加速度的方程:
\(\left. {\begin{array}{*{20}{c}} {\dot \theta \left( t \right) = {a_1} + 2{a_2}t + 3{a_3}{t^2}}\\ {\ddot \theta \left( t \right) = 2{a_2} + 6{a_3}t} \end{array}} \right\}\\)
由于轨迹函数\(\theta (t)\\)至少要满足4个约束条件,所以我们需设置相应的约束:
和
现在有4个方程,可以解出四个待定系数为:
\(\begin{array}{l} {a_0} = {\theta _0};{\rm{ }}{a_2}{\rm{ = }}\frac{3}{{t_f^2}}\left( {{\theta _f} - {\theta _0}} \right){\rm{ }}\\ {a_1} = 0;{\rm{ }}{a_3}{\rm{ = }} - \frac{2}{{t_f^3}}\left( {{\theta _f} - {\theta _0}} \right){\rm{ }} \end{array}\\)
回代到三次多项式中,可得:
\(\theta \left( t \right) = {\theta _0} + \frac{3}{{t_f^2}}\left( {{\theta _f} - {\theta _0}} \right){t^2} - \frac{2}{{t_f^3}}\left( {{\theta _f} - {\theta _0}} \right){t^3}\\)
对其分别求一阶导和二阶导,得到速度和加速度的方程:
\(\begin{array}{l} \dot \theta \left( t \right) = \frac{6}{{t_f^2}}\left( {{\theta _f} - {\theta _0}} \right)t - \frac{6}{{t_f^3}}\left( {{\theta _f} - {\theta _0}} \right){t^2}\\ \ddot \theta \left( t \right) = \frac{6}{{t_f^2}}\left( {{\theta _f} - {\theta _0}} \right) - \frac{{12}}{{t_f^3}}\left( {{\theta _f} - {\theta _0}} \right)t \end{array}\\)
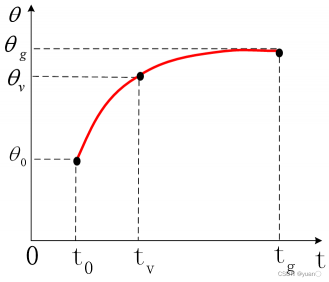
三次多项式插值的运动轨迹曲线如图所示。由图可知,其速度曲线为抛物线,相应的加速度曲线为直线。

由图所示,三次多项式插值得到的加速度曲线为直线,并不连续,需要通过高次多项式才能解决。
3. 过路径点的三次多项式插值
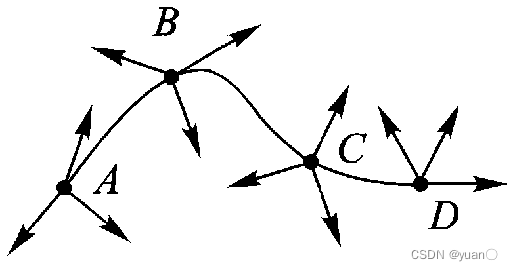
若所规划的作业路径在多个节点上有位姿要求,如图所示,机器人作业除在A、D点有位姿要求外,在路径点B、C也有位姿要求。 对于这种情况,假如车辆在路径点停留,即各路径点上速度为0,则轨迹规划可连续直接使用前面介绍的三次多项式插值方法;但若只是经过,并不停留,就需要将前述方法推广。
进行轨迹规划时,把相邻的两个路径节点分别看做起始点和终止点,再确定相应的三次多项式插值函数,把路径点平滑连接起来。 一般情况下,这些起始点和终止点的关节运动速度不再为零。
设路径点上的节点速度已知,这时,确定三次多项式系数的方法与前所述完全一致,只是速度约束条件变为
\(\left. {\begin{array}{*{20}{c}} {\dot \theta \left( 0 \right) = {{\dot \theta }_0}}\\ {\dot \theta \left( {{t_f}} \right) = {{\dot \theta }_f}} \end{array}} \right\}\\)
利用约束条件可确定三次多项式系数a0,a1,a2和a3,和前面有所不同。但当路径点上的关节速度为0时,确定的三次多项式与上一种方法完全相同,这就说明了这里所确定的三次多项式描述了起始点和终止点具有任意给定位置和速度约束条件的运动轨迹。 总结一下,三次多项式插值方法是:把所有路径点都看成是“起点”或“终点”,确定所要求的三次多项式插值函数,把路径点平滑的连接起来。不同的是,这些“起点”和“终点”的关节速度不再是零。
据此,我们可以求解出各项系数:
\(\begin{array}{*{20}{l}} {{a_0} = {\theta _0};{a_2}{\rm{ = }}\frac{3}{{t_f^2}}\left( {{\theta _f} - {\theta _0}} \right) - \frac{2}{{{t_f}}}{{\mathop \theta \limits^ \bullet }_0} - {t_f}{{\mathop \theta \limits^ \bullet }_f}}\\ {{a_1} = {{\mathop \theta \limits^ \bullet }_0};{a_3}{\rm{ = }} - \frac{2}{{t_f^3}}\left( {{\theta _f} - {\theta _0}} \right) + \frac{1}{{t_f^2}}({{\mathop \theta \limits^ \bullet }_0} + {{\mathop \theta \limits^ \bullet }_f})} \end{array}\\)
由上式确定的三次多项式描述了起始点和终止点具有任意给定位置和速度的运动轨迹。剩下的问题就是如何确定各路径点上的关节速度,有以下三种方法:
- 根据在直角坐标空间中的瞬时线速度和角速度来确定每个路径点的关节速度 ;该方法工作量大。
- 为了保证每个路径点上的加速度连续,由控制系统按照此要求自动地选择路径点的速度
- 在直角坐标空间或关节空间中采用某种适当的启发式方法,由控制系统自动地选择路径点的速度;
对于方法(2),为了保证路径点处的加速度连续,可以设法用两条三次曲线在路径点处按照一定的规则联系起来,拼凑成所要求的轨迹。其约束条件是:联接处不仅速度连续,而且加速度也要连续。
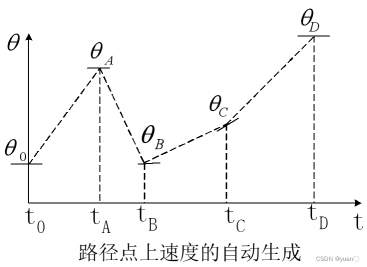
对于方法(3), 这里所说的启发式方法很简单,即假设用直线段把这些路径点依次连接起来,如果相邻线段的斜率在路径点处改变符号,则把速度选定为零;如果相邻线段不改变符号,则选择路径点两侧的线段斜率的平均值作为该点的速度。
4. 用抛物线过渡的线性插值

首先来谈谈单纯的线性插值。单纯的线性插值,有对于给定起始点和终止点的情况选择线性函数插值最为简单的优点;也有会导致起始点和终止点的运动速度不连续,且加速度无穷大,显然,在两端点会造成刚性冲击的缺点。
为了解决其缺点,可以在使用线性插值时,把每个结点的邻域内增加一段抛物线的“缓冲区段”,从而使整个轨迹上的位移和速度都连续。

如图所示,此方法存在多解。加速度的值越大,过渡长度越短。
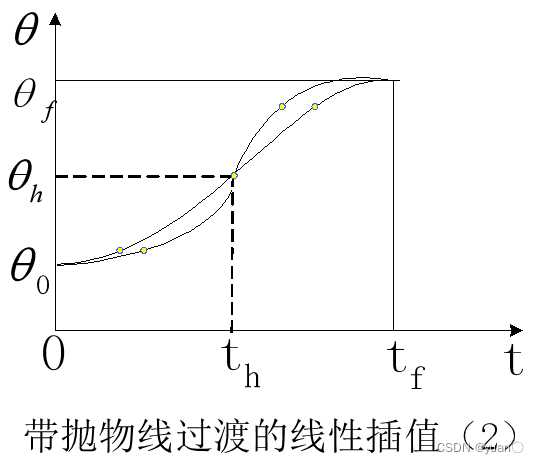
在插值时,通常以线性函数+两段抛物线函数的方式将曲线平滑地衔接在一起,形成带有抛物线过渡域的线性轨迹。为了求解方便,通常设两端的抛物线轨迹具有相同的持续时间\({t_a}\\) ,具有大小相同而符号相反的恒加速度 。此时,会形成一个梯形速度曲线。按照经验,\({t_f}\\)的取值为:\({t_a} = \frac{1}{5}{t_f}\\)

这类轨迹具有多解性和对称性。多解性——这类路径规划存在有多个解,其轨迹不惟一;对称性——每条路径都对称于时间中点\({t_h}\\)和位置中点\({\theta _h}\\)。
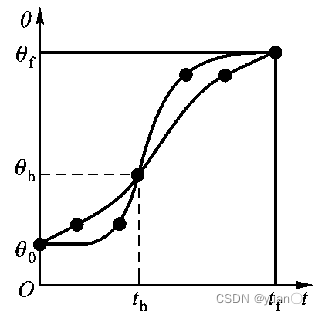
要保证路径轨迹的连续、光滑,即要求抛物线轨迹的终点速度必须等于线性段的速度,故有下列关系:
\(\ddot \theta {t_a} = \frac{{{\theta _h} - {\theta _a}}}{{{t_h} - {t_a}}}\\)与\({\theta _a} = {\theta _0} + \frac{1}{2}\ddot \theta t_a^2\\)
设关节从起始点到终止点的总运动时间为\({t_f}\\),则\({t_f}\\)=2\({t_h}\\),并注意到\({\theta _h} = {\theta _0} + \frac{1}{2}\left( {{\theta _f}-{\theta _0}} \right)\\),从而有\(\ddot \theta t_a^2 - \ddot \theta {t_f}{t_a} + \left( {{\theta _f} - {\theta _0}} \right) = 0\\)。
一般情况下,\({\theta _{\rm{0}}}\\)、\({\theta _f}\\)、\({t_f}\\)是已知条件,可以选择相应的加速度和\({t_a}\\),得到相应的轨迹。通常的做法是先选定加速度的值,然后求出相应的\({t_a}\\):
\({t_a} = \frac{{{t_f}}}{2} - \frac{{\sqrt {{{\ddot \theta }^2}t_f^2 - 4\ddot \theta \left( {{\theta _f} - {\theta _0}} \right)} }}{{2\ddot \theta }}\\)
由上式知,为保证有解,加速度值 必须选得足够大,即
\(\ddot \theta \ge \frac{{4\left( {{\theta _f} - {\theta _0}} \right)}}{{t_f^2}}\\)
当上式中的等号成立时,轨迹线性段的长度缩减为零,整个轨迹由两个过渡域组成,这两个过渡域在衔接处的斜率(关节速度)相等; 加速度的取值愈大,过渡域的长度会变得愈短,若加速度趋于无穷大,轨迹又复归到简单的线性插值情况。
过路径点的用抛物线过渡的线性插值
如图所示,在运动中设有n个路径点,其中三个相邻的路径点表示为j,k和l,每两个相邻的路径点之间都以线性函数相连,而所有的路径点附近则有抛物线过渡。(同样存在多解)
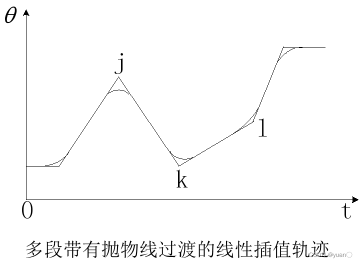
要求机器人通过某个结点,同时速度不为零,可以在此结点两端规定两个“伪结点”,令该结点在两伪结点的连线上,并位于两过渡域之间的线性域上。
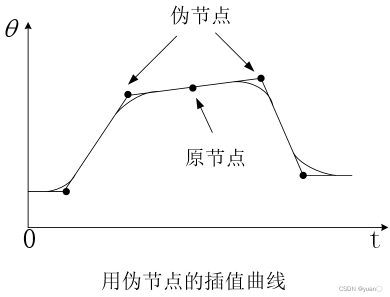
5. 高阶多项式插值
若对于运动轨迹的要求更为严格,约束条件增多,三次多项式就不能满足需要,须用更高阶的多项式对运动轨迹的路径段进行插值。 若对某段路径的起始点和终止点都规定了位置、速度和加速度,则要用一个五次多项式进行插值,即:
多项式的系数a0,a1,…,a5必须满足6个约束条件,即对起始点、终止点的位姿、速度、加速度都作出约束,如下式所示:
\(\left. {\begin{array}{*{20}{c}} {{\theta _0} = {a_0}}\\ {{\theta _f} = {a_0} + {a_1}{t_f} + {a_2}{t_f}^2 + {a_3}{t_f}^3 + {a_4}{t_f}^4 + {a_5}{t_f}^5}\\ {{{\dot \theta }_0} = {a_1}}\\ {{{\dot \theta }_f} = {a_1} + 2{a_2}{t_f} + 3{a_3}{t_f}^2 + 4{a_4}{t_f}^3 + 5{a_5}{t_f}^4}\\ {{{\ddot \theta }_0} = 2{a_2}}\\ {{{\ddot \theta }_f} = 2{a_2} + 6{a_3}{t_f} + 12{a_4}{t_f}^2 + 20{a_5}{t_f}^3} \end{array}} \right\}\\)
声明
本人所有文章仅作为自己的学习记录,若有侵权,联系立删。




评论(0)
您还未登录,请登录后发表或查看评论