一、前言
通过文首的一系列博客，相信大家对于 Homography,Fundamental,Essential 矩阵已经有了一一定认知，比如 单应性Homography 矩阵如下所示(前面的博文有推导,这里的E)为单位矩阵

显的看到，在已知 a,b 摄像头内参的情况下，可以把 F \mathbf FF 转换成 E \mathbf EE 矩阵，然后再进行处理，一般在工程也是这样做的。那么下面就来细致的讨论一下 单应性Homography以及本质 矩阵Essential。

二、Homography
我们首先来看一下单应性Homography矩阵，根据前面的博客，已经知道 Homography矩阵 是由特征点所在平面推导而来，其平面参数就是 (02)式 中的 da,n。竟然是由特征点共面推导而来,那么他的适用场景肯定是特征点共面。

但是这里也存在一个问题，比如: 在三维空间中，有四个特征点共面。并且已知其分别在相机 a,b 的投影(归一化图像坐标)。这样根据两个相机的投影图像，可以获得4对匹配特征点的图像坐标，就可以求解出 H矩阵。那么此时，在投影图像a中选取了一个非共面图像坐标(该坐标对应的三维点，与之前的4个三维点不在同一平面)。使用H矩阵，求解出投影图像b中对应的坐标。

简单的说，就是由共面的4对匹配点计算出来的 H矩阵，应用在不共面的图像坐标上，这个时候，会造成什么样的后果?或者说什么样的误差?这个误差是否可以求解? 求解出来之后我们是否能够纠正呢?

纯旋转
首先从公式入手,观察(01)式，da表示相机坐标系原点a，到共面特征点平面的距离。当 tba=0, 可以发现公式变成如下

非纯旋转
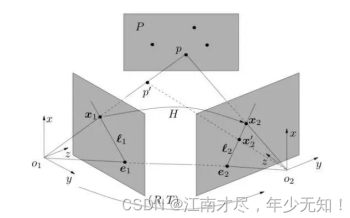
上面讲解的是纯旋转的情况，如果其为非共面点，也非纯旋转，那么会造成什么样的影响呢?如下图所示：

另外:

三、Essential
通过上图，我们可以看到，x2,x2′是位于极线上的，他们的坐标如果都知道，就能够得到极线方程，其上一个 p′确定一条直线，如果还有另外一个非共面的点，那么就能够再确定一条极线。新的图示如下：

如果能够确定联调极线，那么极点 e2也就被确定了，极点确定了, H21也知道，那么不使用本质矩阵，也可以构建极线几何了。则就是所谓的六点法。四个共面的点确定H，再由两个非共面的点确定极点。

但是八点法计算求解本征矩阵不能应用于共面的情形，利用向量叉乘自己结果为 0这条性质即可推导：
x2 = H21x1 ⇒ x2 H21 x1 = 0 (07)
其上，我们可以
另外，任意三维向量 v和 x2的叉乘肯定垂直于向量 x2，且由于共面，所以有:

四、结语
通过该篇博客主要分析了 Homography矩阵 以及 Essential矩阵 的使用场景。所以在工程中，四需要根据实际情况选取所需的公式。不然有可能会造成未知的误差