前面从两种思路讨论了轨迹优化问题的求解：

  1. 从解析法求解得到微分方程，进而推导出轨迹拟合问题；
  2. 从数值法求解得到代数方程，进而推导出轨迹插值问题。

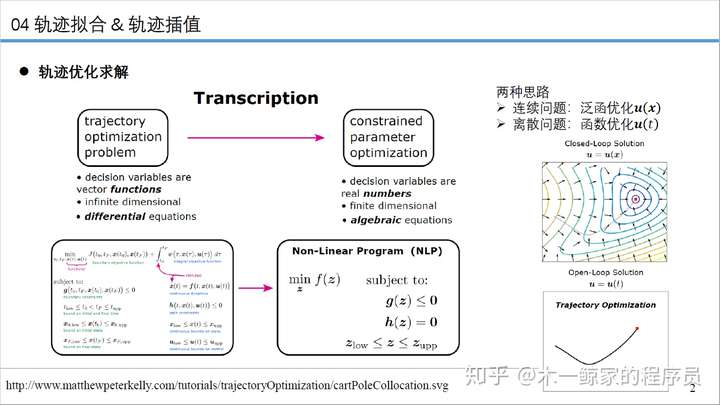
本篇具体讨论一下两种思路的共同点与不同点

1. 轨迹拟合

这里罗列了主流的一些解析法求解的方法和结论（博主的数学比较差，实在是不想去具体讨论推导，就只列出了结论，在轨迹优化02中也只是简单考虑了无约束条件泛函极值的求解）

我们知道，这些结论最终都把轨迹优化问题指向了微分方程，而微分方程的求解又涉及到函数空间，函数空间中主要工具是正交多项式（这里也不去讨论正交化等细节问题），我们需要知道的是两种重要的正交函数：

(1)多项式

(2)三角函数

这也是我们为啥在轨迹规划伊始就提到了我们要用三次多项式、五次多项式、三角函数等去进行拟合

2. 轨迹插值这里罗列了两种主要的数值法求解的过程和结论：

这些结论最终都把轨迹优化问题指向了代数方程，求解NLP问题，通过配置点形成了插值空间，而主要的插值方法是三次插值

求解三次插值有两类问题：(1)中间点的速度已知，这个问题就是求解分段三次多项式

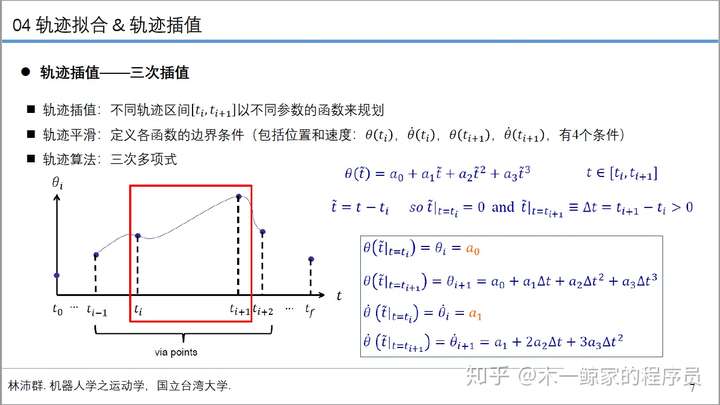
(2)中间点的速度未知，这个问题就是经典的三次样条问题

3. 轨迹拟合 & 轨迹插值 汇总

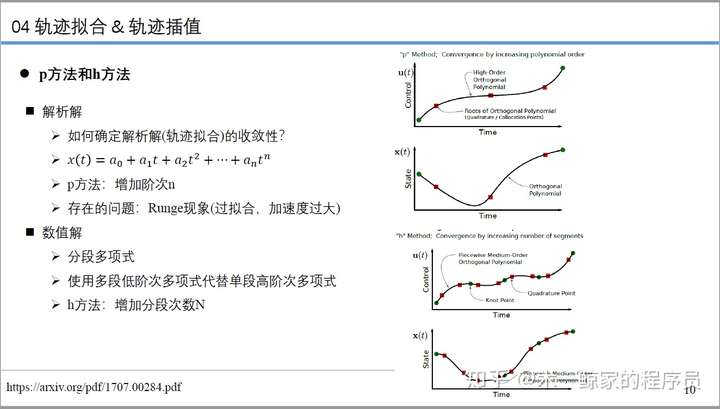
4. Runge现象

这个问题无论是机器学习（过拟合），还是说插值与拟合（Runge现象），还是说轨迹优化问题（加速度过大），其实都是一类问题：为了拟合的收敛性，必须增大拟合的阶次（p方法）

在插值中，通常采用增加分段（h方法），来降低多项式阶次，从而解决这个Runge现象

Reference

  1. matthewpeterkelly.com/t
  2. 林沛群. 机器人学之运动学，国立台湾大学
  3. arxiv.org/pdf/1707.0028

写在后面：

在本专栏中，很多问题我并没有讲的很明白，主要还是笔者的水平有限，希望读者见谅，写这些主要目的是给自己留个笔记的

如果有读者不明白的地方，欢迎一起交流或者带着“关键词”去寻找更系统和完备的解答