引言

支持向量机作为一个有着完整理论证明并且效果很棒的算法始终活跃在机器学习的舞台上，而博主也很早就知道支持向量机了，但是始终都只是调用一下别人写的算法，没有深入的去理解支持向量机的原理，正好林轩田教授的机器学习技法课程一上来就介绍了svm这个经典算法，好好学习一下。

什么是svm

这个名字总会引起大家的误会，第一次听说会有一种不明觉厉的感觉，好像某种神奇的机器一样。不要被它的名字吓到，因为支持向量机的原理说白了很简单。

最好的超平面

svm最初使就是作为一个线性分类器诞生的，所以我们给一组线性可分的数据。

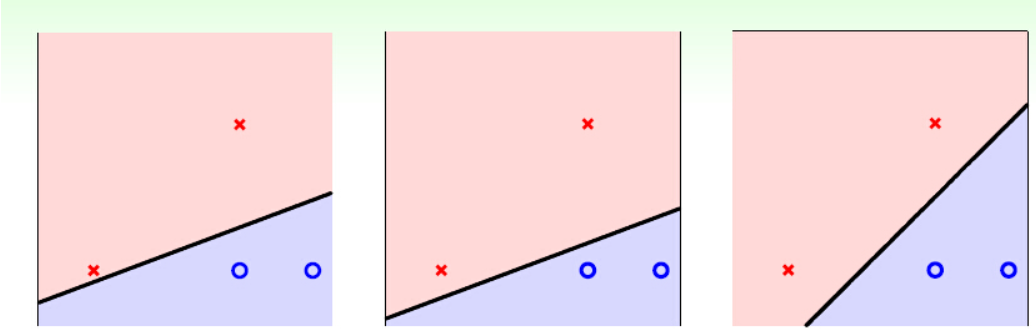
上面的三幅图其实是对这四个二维空间点的三种线性分类的方法，如果你使用PLA一类的线性分类方法，这三条线是都有可能出现的（PLA具体原理说白了就是用分类错误的数据来更新权重，所以不同的输入顺序会导致不同的线）。而很明显，这三条线看起来是有好有坏的，而到底哪个是最好的呢？svm就是去寻找最好得一条线的。当然二维空间是线，多维空间就成了超平面（hyperplane）。
当然好坏的区分需要我们制定一个标准，svm中的标准就是这个平面要离被分开的两组数据都尽量的远。

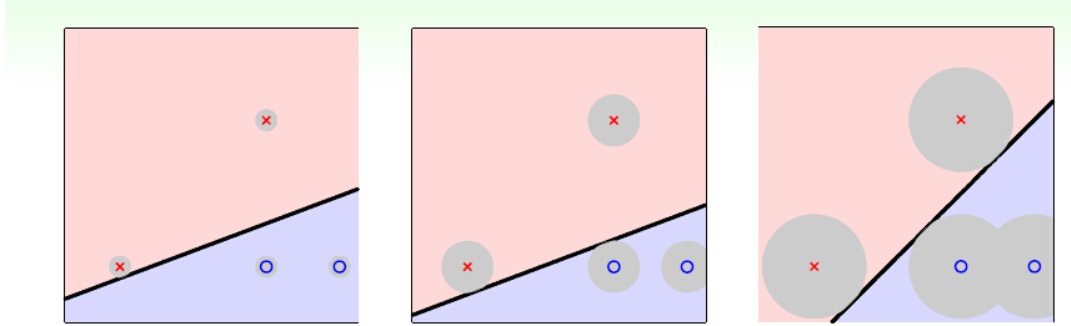
上图明显可以看出，第三个图中的线离被分开的数据最远。

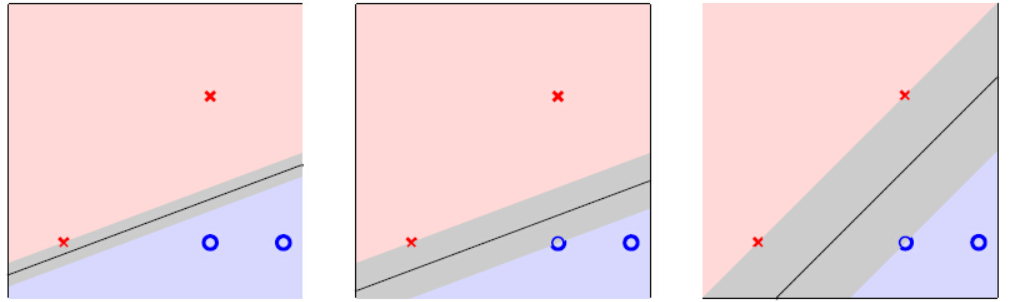
其实可以换一种解释，我们要找两类数据点间‘最胖’的空间，如上图左三。
而最胖空间的中的那条线（超平面）也就是最好的超平面。而术语中，“胖”我们 成为margin，也就是找一个有最大的边界超平面，来分割数据。
目标：

最大超平面的距离

我们需要找最大的margin，其实也就是找到一个最大的点到超平面的距离（当然是边界点，也被称为支持向量）。

超平面可以简单地表示为上面的公式，x表示数据点，w，b是超平面的参数。
实际上w就是超平面的一个法向量，而点面距离可以简单地表示成：

即为点面连线到法向量上的投影。
所以我们的目标可以写为：

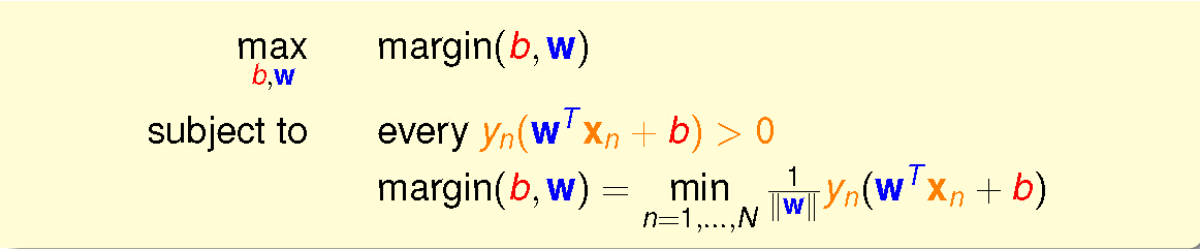
也就是将上面的目标中的距离表示具体化。
而超平面实际是可以乘一个尺度因子的，并不会影响超平面的表示：

上式就是用了一个特殊的尺度因子，目标问题简化为：

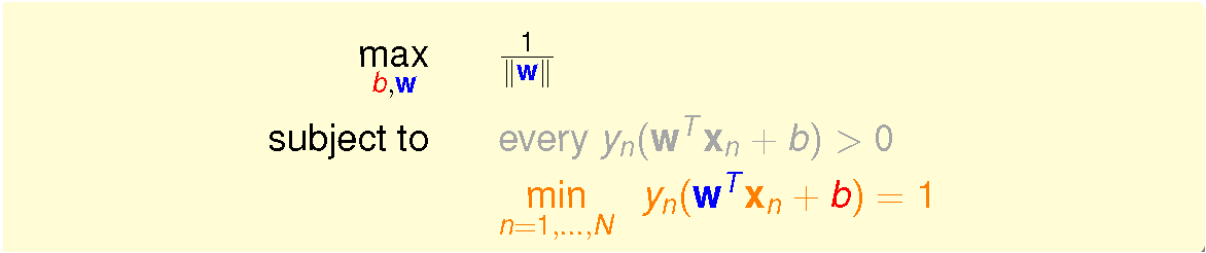
而两个条件是可以合并的，可以进一步简化为：

而最大化问题我们呢常常会变成最小化问题，并且条件对于所有点来说可以变的更宽松：

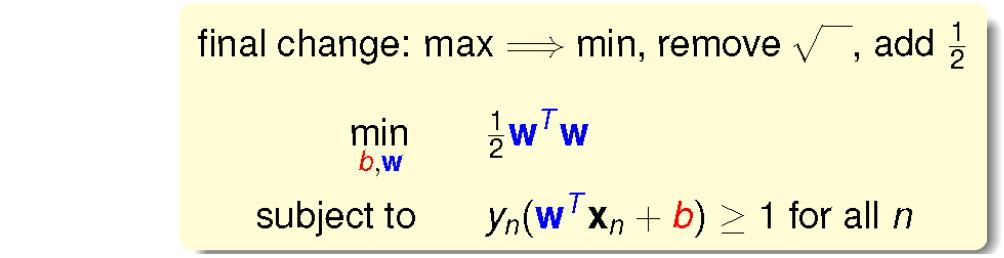
而这个问题的解决方法可以转化为一个二次规划问题：

最后你只需要把参数塞进一个QP solver就ok啦！！

小结

这篇文章介绍的方法是hard margin svm，我们求出的边界是不允许有误差项出现的，也就是数据必须要线性可分才可解，当然大师们早已想好了解决方案~后面再继续学习svm的各种变形方法，用来对付非线性数据和噪声~~
ps:最近真的是挺懒的，这篇文上拖拖拉拉搞了快一周了~后面要更勤奋呀~