差速轮机器人时间最优控制
最优控制做为现代控制理论一个非常重要的部分,相比于其它控制算法,直接对性能指标进行优化,同时可以添加各种各样的约束条件等优点,在自动化工程中有比较多的应用。但受限于当前的计算水平,还没有传统控制算法普遍应用于实际生产、生活中。
本文将通过离散化的方式求解差速轮机器人从点A(x ,y ,θ ),运行到点B的时间最短,在运行过程中,有速度、加速度的约束。
差速轮机器人运动学
由于最优控制需要预测差速轮机器人的状态,因此需要得到差速轮机器人的运动学模型,其中微分形式的状态方程如式(1)所示。

式(1)中,( x , y , θ ) 为机器人在平面上的位姿,( v , w )分别为机器人的线速度和角速度,( a v , a w ) 分别为机器人的线速度加速度和角速度加速度,也就是需要控制的变量。由于本文不使用极小值或动态规划的方法求解该问题(通常无解),而是采用离散化近似的方法求解该问题,因此需要根据式(1)得到离散化形式的状态方程,如式(2)所示。

目标函数
在定义目标函数前,需要确定优化的目标,比如当机器人到达终点时,机器人和目标点的位姿偏差尽可能小,同时速度和加速度在约束范围内。由此可定义目标函数如式(3)所示。
实验效果如下图所示:
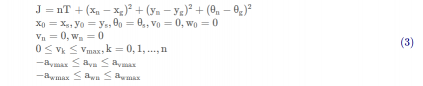
式(3)中,( x s , y s , θ s ) 为起始点位姿,( x g , y g , θ g )为终点位姿。当将( a v 0 , a w 0 , a v 1 , a w 1 , . . . , a v n , a w n , T ) 作为变量时,可以式(2)计算相关的状态,也就得到非线性离散状态的目标函数。
实例求解
由于方程(3)是一个多变量非线性优化的问题,本文将使用casadi求解器进行求解,并用ROS当中的rviz进行可视化显示,实际程序如下所示,其中以(-1,1,0)为起点,(0,0,0)为终点。
# -*- coding: utf-8 -*-
import numpy
import casadi as ca
import matplotlib.pyplot as plt
import math
import rospy
import numpy as np
import time
from geometry_msgs.msg import Twist
from sensor_msgs.msg import PointCloud
from geometry_msgs.msg import Point32
from geometry_msgs.msg import PoseWithCovarianceStamped
from geometry_msgs.msg import PoseStamped
fig = plt.figure()
ax1 = fig.add_subplot(111)
#ax1.set_title('Fig')
plt.xlabel('x(m)')
plt.ylabel('y(m)')
g_pub_clothoid = rospy.Publisher('/trajectory', PointCloud, queue_size = 2)
def solveProblem():
print_time = rospy.Time().now().to_sec()
N = 51
U = ca.SX.sym('U', N)
x0 = ca.SX.sym('x0', 5) #初始条件
x0[0] = -1
x0[1] = 1
x0[2] = 0
x0[3] = 0
x0[4] = 0
xf = ca.SX.sym('xf', 5) #终端状态
xf[0] = x0[0]
xf[1] = x0[1]
xf[2] = x0[2]
xf[3] = x0[3]
xf[4] = x0[4]
obj = U[-1]
g = []
det_t = ca.SX.sym('det_t', 1)
det_t = U[-1] / ((N - 1) / 2)
for i in range((N - 1) / 2):
xf[4] += det_t * U[2 * i + 1]
xf[3] += det_t * U[2 * i]
xf[2] += det_t * xf[4]
xf[1] += det_t * xf[3] * ca.sin(xf[2])
xf[0] += det_t * xf[3] * ca.cos(xf[2])
g.append(xf[0])
g.append(xf[1])
g.append(xf[2])
g.append(xf[3])
g.append(xf[4])
nlp_prob = {'f': obj, 'x': U, 'g': ca.vertcat(*g)}
opts_setting = {'ipopt.max_iter':100, 'ipopt.print_level':0, 'print_time':0, 'ipopt.acceptable_tol':1e-8, 'ipopt.acceptable_obj_change_tol':1e-6}
solver = ca.nlpsol('solver', 'ipopt', nlp_prob, opts_setting)
lbx = []
ubx = []
lbg = []
ubg = []
for i in range((N - 1) / 2):
lbx.append(-1)
ubx.append(1)
lbx.append(-3)
ubx.append(3)
lbx.append(0)
ubx.append(100)
for i in range(5):
lbg.append(0) #终端约束
ubg.append(0) #终端约束
res = solver(lbx = lbx, ubx = ubx, lbg = lbg, ubg = ubg)
print('cost time of casadi opt problem: ', rospy.Time().now().to_sec() - print_time)
print(res['f'], res['x'])
#print(xf)
UU = res['x']
points = PointCloud()
points.header.frame_id = 'map'
xf[0] = x0[0]
xf[1] = x0[1]
xf[2] = x0[2]
xf[3] = x0[3]
xf[4] = x0[4]
points.points.append(Point32(xf[0], xf[1], 0))
det_t = ca.SX.sym('det_t', 1)
det_t = UU[-1] / ((N - 1) / 2)
for i in range((N - 1) / 2):
xf[4] += det_t * UU[2 * i + 1]
xf[3] += det_t * UU[2 * i]
xf[2] += det_t * xf[4]
xf[1] += det_t * xf[3] * ca.sin(xf[2])
xf[0] += det_t * xf[3] * ca.cos(xf[2])
points.points.append(Point32(xf[0], xf[1], 0))
g_pub_clothoid.publish(points)
# #while not rospy.is_shutdown():
for i in range(100000):
g_pub_clothoid.publish(points)
#rospy.sleep(0.1)
print('end pub')
if __name__ == '__main__':
print('opt control test.')
rospy.init_node("opt_control_test", anonymous = True)
solveProblem()
rospy.spin()
复制实验效果如下图所示:
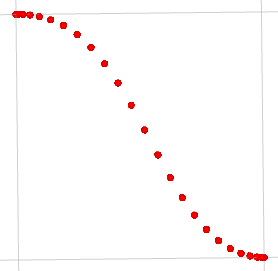
注意事项
- 本文只提供一个近似的解;
- 变量的个数越多,求解越经精确,但计算量也就越大;
- 需要在ROS环境下运行;
- 需要安装casadi库;
- 当前计算实时性非常差,不适合做为路径跟踪控制器;






评论(0)
您还未登录,请登录后发表或查看评论