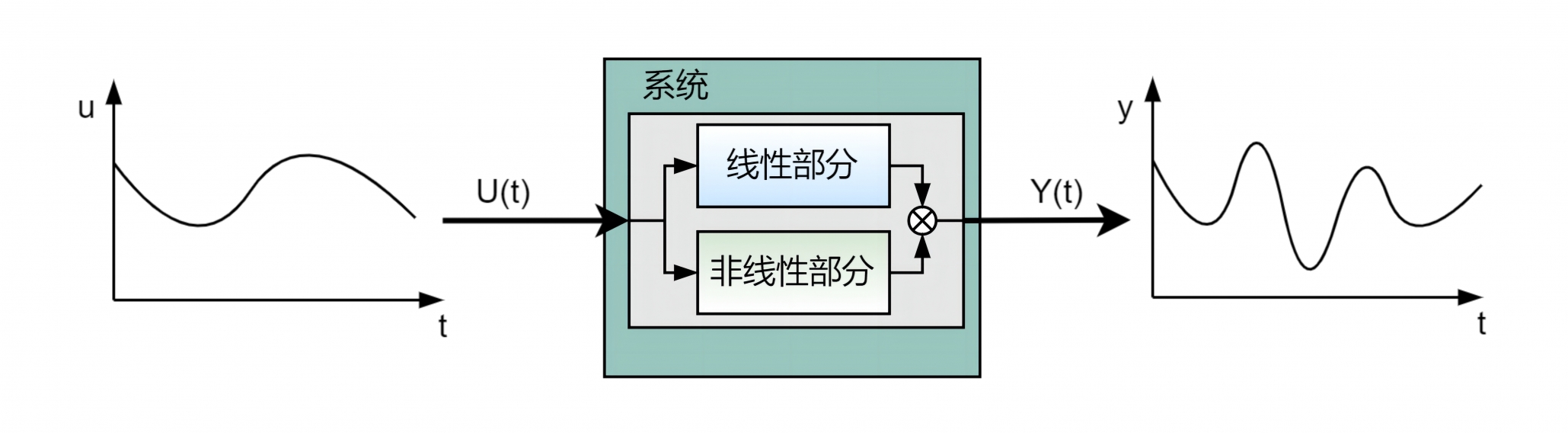
在信息科学技术飞速发展的时代，工业生产规模越来越大，工艺、设备和过程越来越复杂，传统的建模方法已经很难达到对时间生产过程的精确控制。现代工业往往由多个生产过程有机联接，复杂程度较高，同时过程关键特性或者中间变量收到原料成分、运行工况、设备状态等多种不确定因素的干扰，容易随着生产环境的改变而改变，因此对其进行分析、建模、优化与控制都会面临极大的困难。所以建立准确、稳定的复杂工业过程预测模型可以更清晰的掌握过程的运行状态，为后续过程控制及优化奠定基础，所以复杂工业过程的建模放大研究有着极大的必要性和重要性。

       由于工业过程比较复杂，不能用理论分析的方法获得数学模型，凡是需要通过实验数据确定数学模型和估计参数的场合都要利用辨识技术，辨识技术已经推广到工程和非工程的许多领域，例如化学化工过程、电力系统、航空航天飞行器、生物医学系统、花茎系统、生态系统等。系统辨识是根据系统的实验数据来确定系统的数学模型，系统辨识为已经存在的系统建立数学模型提供了有效的方案。

系统辨识

       系统辨识通俗的讲是被控对象或被辨识系统的输入、输出观测信息来估计它的数学模型。辨识有三个要素，及数据、模型类和准则，数据是便是的基础，准则是辨识的依据，模型类是辨识的范围，辨识就是按照一个准则在一组模型类中选择一个对数据拟合的最好的模型。

       复杂工业过程的运行指标由过程控制闭环系统的输出和运行指标之间的动态模型组成，但是过程系统的输出与运行指标之间的机理不清，具有强非线性，难以建立精确的数学模型。过程控制系统的输出对运行指标的影响，他们之间的动态模型可以描述为：

在上式中， $d$ 为延时， $u(k)$ 是输入， $n_{A}$ 和 $n_{B}$ 是运行指标模型的阶次， $f(\cdot){\in}R$ 是未知的非线性函数。

令

$\varphi(k-d)$ 是维数为 $p=n_A+n_B+1$ 的数据向量，则式(1)可以表示

一般情况下，运行指标在工作点附近工作，从而可以将运行指标在工作点附近表示成由线性模型和非线性模型和的形式，通过将运行指标在工作点线性化就可以得到。假设工作点在原点，通过 Taylor展开，得到多项式 $A(z^{-1})$ 和 $B(z^{-1})$ 的表示形式如下：

则可以得到运行指标的动态模型在工作点即原点附近的等价模型：

在上式中， $v[\varphi(k-d)]$ 表示高阶非线性函数，称为未建模动态。设 $d=1$ ,则上式的运行指标的预报模型可以写为：

通过上式可以进行一步预报。但是在上式中，由于 $v[\varphi(k)]$ 未知，要进行运行指标的一步预报值则需要首先对 $k$ 时刻的未建模动态 $v[\varphi(k)]$ 进行估计。当模型(7) 中的 $A\left(z^{-1}\right)$ 和 $B(z^{-1})$ 已知，则 $v[\varphi(k)]$ 的准确估计是影响运行指标的关键。但是若 $A\left(z^{-1}\right)$ 和 $B(z^{-1})$ 未知，则不仅要估计未建模动态 $v[\varphi(k)]$ , 还要估计多项式 $A(z^{-1})$ 和 $B(z^{-1})$ 的参数。

当运行指标模型(7)中的 $A(z^{-1})$ 和 $B(z^{-1})$ 已知时，对 $v[\varphi(k)]$ 进行估计时，为了突出算法的原理，选择用最常用的多层感知器（Multilayer Perceptron，MLP）神经网络对 $v[\varphi(k)]$ 进行估计， 然后再考虑 $A\left(z^{-1}\right)$ 、 $B\left(z^{-1}\right)$ 和 $v\left[\varphi(k)\right]$ 均末知时的非线性模型辨识算法。

在上式中，

虽然 $\bar{A}(z^{-1})$ 和 $B(z^{-1})$ 已知，但是 $y(k+1)$ 是末知的，所以 $v[\varphi(k)]$ 是未知的。因为 $v[\varphi(k)]$ 是高阶的非线性函数，通过采用MLP神经网络的方法对 $v[\varphi(k)]$ 进行估计，可以得到相应的估计值 $\hat{v}[\varphi(k)]$ 。将 $u(k)$ 作用于运行指标模型(7) 可以得到一步预报值 $y(k+1)$ ,由式(8)可以得到：

由此可以得到神经网络的导师信号为：

通过数据向量 $\varphi(k)$ 以及导师信号 $v[\varphi(k)]$ 对神经网络进行训练产生下一时刻的估计值 $\hat{v}[\varphi(k)]$ 。

下面介绍对在实验过程中用到的最小二乘算法、递推最小二乘算法；并介绍了在线性模型参数未知时的交替辨识算法。

最小二乘算法

       在系统辨识和参数估计领域中，最小二乘方法作为一种最基本的估计方法应用极为广泛，其它的大多数估计算法都与最小二乘有关，它既可以用于动态系统，也可以用于静态系统； 可用于线性系统，也可用于非线性系统； 可用于离线估计，也可用于在线估计。

考虑如下形式的离散时间随机线性模型：

式中， $u(k)$ 和 $y(k)$ 分别为被控对象的输入和输出变量， $\xi(k)$ 是白噪声， $d$ 是被控对象时延， $A({z^{-1}})$ 、 $B({z^{-1}})$ 和 $C({z^{-1}})$ 是具有如下形式的后移算子多项式：

式中， $n_A,n_B,n_c$ 分别为 $A\left(z^{-1}\right)$ 、B $\left(z^{-1}\right)$ 、C $\left(z^{-1}\right)$ 多项式的阶次，为已知正整数 $a_i\left(i=1,\cdots n_A\right)\text{、}b_j\left(j=0,\cdots,n_B\right)\text{、}c_l\left(l=1,\cdots,n_c\right)$ 为 $A\left(z^{-1}\right)\text{、B}\left(z^{-1}\right)\text{、C}\left(z^{-1}\right)$ 的未知系数。

当 $C(z^{-1})=0$ 时，表示确定性线性模型；当 $C(z^{-1})=1$ ,表示受到白噪声干扰的随机线性模型。以受到白噪声干扰的随机线性模型为例：

定义 $p=n_A+n_B+1$ 维的数据向量 $\varphi(k-1)$ (己知)和参数向量 $\theta$ (未知)为

则被控对象又可以表示为：

就是通过已经测量到的输入和输出序列，求得待估计的参数，并且使估计误差按照某一规则最小。采用一次完成估计的最小二乘估计算法如下：

通过确定参数向量 $\theta$ ,使得在最小二乘意义上，由 $\varphi^{\mathrm{T}}(k-1)\theta$ 算出的输出应该尽可能的与实测变量 $y(k)$ 接近，即使得残差平方和最小，估计准则为

记由 N 次观测的数据得到的对未知参数 $\theta$ 的估计为 $\hat{\theta}$ ,那么，对于第 $i$ 次观测，实际观察值 $y(i)$ 与估计模型计算值 $y_m(i)=\varphi^{\mathrm{T}}(i-1)\hat{\theta}$ 之间的偏差为

$\varepsilon(i)$ 称为残差。引入记号

则有如下表示：

综上，残差 $\varepsilon_N$ 取决于参数拟合误差 $\left(\theta-\hat{\theta}\right)$ 和过程噪声 $\xi_N$ 。则最小二乘目标函数可以重新表示为

目标就是求得极小的 $\hat{\theta}$ ,该值称为未知向量 $\theta$ 的最小二乘估计。

递推最小二乘算法

递推最小二乘算法的思想可以概括成：

采用递推最小二乘辨识可以减少计算量和存储量，而且能够实现在线辨识。 未知参数向量 $\theta$ 的最小二乘估计 $\hat{\theta}_{Ls}$ 的递推计算公式为：

在上式中，

递推最小二乘算法的步骤归纳如下：

1. 置初值 $\hat{\theta}(0)=0$ , $P(0)=10^6I$ ;
2. 构造数据向量 $\varphi(k-1)=\left[-y(k-1),-y(k-2),\cdots,-y(k-n_A),u(k-d),u(k-d-1),\cdots,u(k-d-n_B)\right]^T$
3. 进行第 $k$ 次采样，得到 $y(k);$
4. 由(26)式计算 $K(k);$
5. 由(25)式计算 $\hat{\theta}_{LS}(k);$
6. 由(27)式计算 $P(k)$ ;
7. 递推一步 $k+1{\to}k$ ,并返回步骤 (2), 构造新的数据向量。

线性模型参数未知时的交替辨识算法

       由于工业现场的复杂性，工业生产规模越来越大，工艺、设备和过程越来越复杂，导致运行指标难以建立精确的数学模型，所以 $A\left(z^{-1}\right)$ 和 $B\left(z^{-1}\right)$ 以及未建模动态 $v[\varphi(k)]$ 均未知，针对此情况，需要首先采用参数辨识算法辨识系统参数，对为建模动态采用MLP神经网络进行估计，实现对整个运行指标模型的辨识。由式子(7)和(8)可以得到：

从式(30)可以得到，由于 $A\left(z^{-1}\right)$ 和 $B(z^{-1})$ 未知，所以 $v[\varphi(k)]$ 未知。在进行辨识的时候，首先对 $A\left(z^{-1}\right)$ 和 $B(z^{-1})$ 赋予初值，可以得到 $v\left[\varphi(k)\right]$ 的估计值，然后将得到的 $v[\varphi(k)]$ 的估计值作为神经网络的导师信号，采用神经网络对 $v[\varphi(k)]$ 进行估计，从而得到其估计值 $\hat{v}[\varphi(k)]$ ,然后将该式带入到式子(31)中，并采用最小二乘法辨识 $A\left(z^{-1}\right)$ 和 $B\left(z^{-1}\right)$ ,从而得到 $A\left(z^{-1}\right)$ 和 $B(z^{-1})$ 的辨识值 $\hat{A}(z^{-1})$ 和 $\hat{B}(z^{-1})$ ,然后再将 $\hat{A}(z^{-1})$ 和 $\hat{B}(z^{-1})$ 带入到式子(30) 中，可以获得下一时刻的导师信号，即

然后再通过下一时刻的数据向量 $\varphi(k)$ 的估计值，进行反复计算。即采用估计 $\left\{A\left(z^{-1}\right),B\left(z^{-1}\right)\right\}$ 的最小二乘算法与 $v[\varphi(k)]$ 的神经网络估计算法的交替辨识的方法对非线性模型(7) 进行辨识。

综上所述， $v[\varphi(k)]$ 的神经网络估计的导师信号方程和估计 $\left\{A(z^{-1}),B(z^{-1})\right\}$ 的参数辨识方程如下所示：

为了辨识 $A\left(z^{-1}\right)$ 和 $B(z^{-1})$ ,将辨识方程写成如下形式：

在该式子中，

是 $k-1$ 时刻对参数 $\theta=\left[-\alpha_1,-\alpha_1,\cdots,-\alpha_{n_A},b_0,b_1,\cdots b_{n_B},\right]^T$ 的估计值，采用最小二乘法进行估计。

最后，把 $\hat{A}(z^{-1})$ 和 $\hat{B}(z^{-1})$ 的估计值代入式子(32),获得 $v[\varphi(k)]$ 的神经网络的估计算法的导师信号 $\overline{v}[\varphi(k)]$ ,再构建下一时刻的数据项，采用MLP神经网络估计算法对 $v[\varphi(k-1)]$ 进行估计，将获得的估计值 $\hat{v}[\varphi(k-1)]$ 代入 $\left\{A\left(z^{-1}\right),B\left(z^{-1}\right)\right\}$ 的参数辨识方程,采用最下二乘法对 $\left\{A\left(z^{-1}\right),B\left(z^{-1}\right)\right\}$ 进行辨识。

当系统动态模型完全未知的情况下，采用交替辨识算法进行系统辨识的框图如图所示。

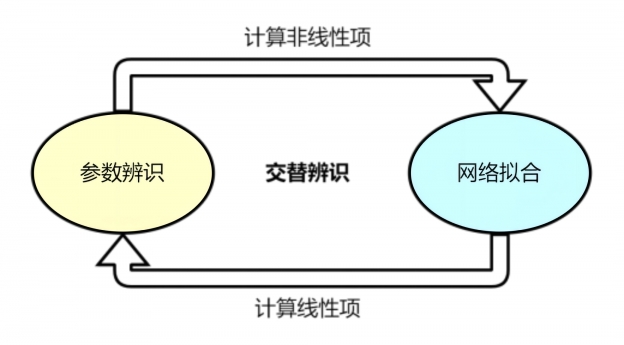
针对上述非线性模型辨识算法的步骤总结如下：

1. 对 $A({z^{-1}})$ 和 $B({z^{-1}})$ 赋予初值，即给定初值 $\hat{\theta}(0);$
2. 根据选定 $\left\{A(z^{-1}),B(z^{-1})\right\}$ 的初值，获得与 $\left\{A\left(z^{-1}\right),B\left(z^{-1}\right)\right\}$ 的初值相对应的神经网络的导师信号 $\overline{v}[\varphi(k)];$
3. 测取 $y(k),\cdots,u(k),\cdots$ ,构成数据向量 $\varphi(k)$ ,并与导师信号 $\overline{v}[\varphi(k)]$ 训练神经网络，获得 $v[\varphi(k)]$ 的估计值 $\hat{v}[\varphi(k)];$
4. 将估计值 $\hat{v}[\varphi(k)]$ 代入 $\left\{A(z^{-1}),B(z^{-1})\right\}$ 的参数辨识方程，然后采用最小二乘辨识算法估计 $\begin{Bmatrix}A(z^{-1}),B(z^{-1})\end{Bmatrix};$

5. 然后求下一时刻神经网络输出层和隐含层的权值；
6. 返回步骤 3),估计下一时刻的 $\left\{A\left(z^{-1}\right),B\left(z^{-1}\right)\right\}$ 和 $v\left[\varphi(k)\right]$ 。

仿真实验

针对如下系统，建立低阶线性模型与非线性项智能补偿模型的混合模型，

建模形式为：

仿真模型选择的形式如下：

原点是系统的平衡点，则各部分的表达式如下：

对于线性部分，即参数 $\theta=\left[a_1,a_2,b_0,b_1\right]^{T}$ ,采用了增广递推最小二乘辨识的方法； 对于非线性项 $v[\varphi(k)]$ 采用了MLP神经网络辨识来建立未建模动态的动态模型。

在仿真中，选择输入信号为：

参数的初始状态为：

选择MLP神经网络来建立未建模动态的动态模型时，网络的输入为数据向量 $\varphi(k)$ ,根据数据的维度设计网络参数，MLP神经网络的隐含层节点数 $l=32$ ,隐层所用的激活函数为ReLU函数，学习率 $lr=0.01$ ,动训练方法采用SGD, 最大迭代轮数为 1000轮，当均方误差到达1 $e^{-4}$ 时停止训练，将数据向量 $\varphi(k)$ 作为输入，误差项作为输出，进行网络训练。

下面进行具体实现：

首先将非线性项作为扰动，利用递推最小二乘算法进行辨识，将辨识结果作为系统线性项辨识的初值，这样可以使交替算法在尽可能少的迭代中收敛，仿真结果如图所示：

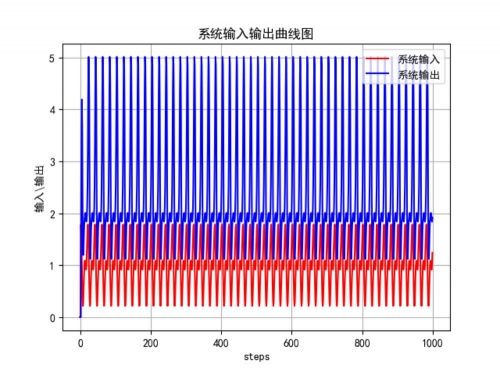
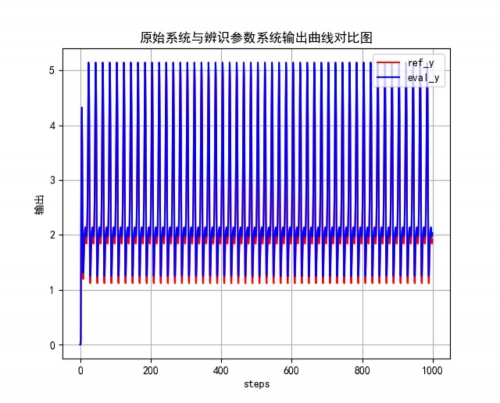
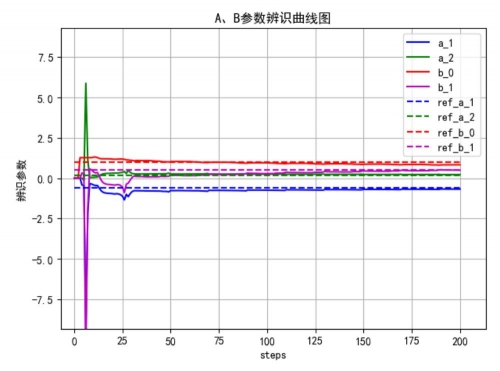
交替系统辨识的效果图，图中虚线表示的是真实值，实线表示的是预测值，从图中可以看到，参数的真实值和估计值较为接近，采用该方法得到的均方误差小于 $1e^{-4}$ ，则可以体现估计的误差非常小，体现了交替辨识算法的有效性。

总结：

       整个过程可以称为数据-机理融合建模，通过融合机理和数据的特点，提高了建立模型的准确性。通过机理建模我们可以理解系统内部的物理机制，而数据建模能够从大量的实际运行数据中学习出模型的参数和结构。这种混合模型的优势在于结合了两种建模方法的优势，使得模型更加准确、可靠。在实际应用中，我们可以利用混合模型来进行系统的控制和优化。通过对线性部分进行控制器设计，我们可以实现对物理系统的精确控制。同时，通过数据模型对机理模型的误差进行在线补偿，我们可以使得控制器更加鲁棒，能够适应系统的变化和不确定性，实现对物理系统的精确控制。

在交替辨识时，要注意进行线性与非线性输出的解耦：

其中 $y_{all}=y_{linear}+y_{nonlinear}$ ，所以在计算线性及非线性的导师信号时，注意要减去对应的 $y_{linear}、y_{nonlinear}$ 将线性与非线性分开，这样才能保证辨识出的线性参数准确。

代码

交替辨识

import matplotlib
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt

from RLS import my_recursive_least_squares

# 设置全局字体参数
font = {'family': 'sans-serif', 'sans-serif': ['SimHei']}
matplotlib.rc('font', **font)
matplotlib.rc('axes', unicode_minus=False)  # 禁用负号的Unicode字符
# 定义输入序列
N = 1000  # 迭代次数

# 初始化输出序列
# y = np.zeros(N)
u = np.zeros(N)
e = np.zeros(N)
y_line_out = np.zeros(N)
y_nonlinear_out = np.zeros(N)
y_out = np.zeros(N)
# y[0] = 0
# y[1] = 0
A_coeff = np.array([1, -0.6, 0.2])
B_coeff = np.array([1, 0.5])
d = 1
na = len(A_coeff) - 1
nb = len(B_coeff) - 1
nu = na + nb + 1
y_c_matrix = np.zeros(na)
u_c_matrix = np.zeros(nb + d)
# 生成数据
for k in range(2, N):
    u[k] = 1 + 0.4 * np.sin(k / 5 * np.pi) + 0.5 * np.cos(k / 10 * np.pi)
    u_c_matrix[0] = u[k - 1]
    u_c_matrix[1] = u[k - 2]
    # y[k] = 0.6 * y[k - 1] - 0.2 * y[k - 2] + u[k - 1] + 0.5 * u[k - 2]
    y_c_matrix[0] = y_out[k - 1]
    y_c_matrix[1] = y_out[k - 2]
    y_nonlinear_out[k] = 0.5 * np.sin(u[k - d] + u[k - d - 1] + y_out[k] + y_out[k - 1])
    y_line_out[k] = -A_coeff[1:] @ y_c_matrix + B_coeff @ u_c_matrix
    y_out[k] = y_line_out[k] + y_nonlinear_out[k]


def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val):
    for epoch in range(1, n_epochs + 1):
        t_p_train = model(t_u_train)
        loss_train = loss_fn(t_p_train, t_u_val)

        optimizer.zero_grad()  # 梯度清零
        loss_train.backward()  # 利用前向图计算梯度
        optimizer.step()  # 利用梯度，更新参数

        if epoch % n_epochs == 0:
            print(f"Training loss {loss_train.item():.4f}")
    return model, loss_train


train_model = nn.Sequential(
    nn.Linear(4, 32),
    nn.ReLU(),
    nn.Linear(32, 32),
    nn.ReLU(),
    nn.Linear(32, 1))
optimizer = optim.SGD(train_model.parameters(), lr=1e-2)

u_train = np.zeros((4, N))
for i in range(2, N):
    u_train[0][i] = y_out[i - 1]
    u_train[1][i] = y_out[i - 2]
    u_train[2][i] = u[i - 1]
    u_train[3][i] = u[i - 2]

t_u_train = torch.tensor(u_train[:, :N].T, dtype=torch.float)
t_u_val = torch.tensor(y_nonlinear_out[:N], dtype=torch.float).unsqueeze(1)

"""---------------------系统辨识--------------------------"""
Theta = np.zeros((nu, 1))  # Initial Parameters
P = 10 ** 6 * np.eye(nu)  # Initial Covariance Matrix
Phi = np.zeros((N, nu))  # Initial phi
a = np.zeros((na, N))
b = np.zeros((nb + 1, N))
K = np.zeros((nu, N))
coeff1 = 0
coeff2 = 0

alter_y_linear = np.zeros(N)
alter_y_nonlinear = np.zeros((1, N))
train_flag = True
train_L = 0

for i in range(2, N):
    train_L = i
    offset_factor = coeff1 * alter_y_nonlinear[0][i - 1] + coeff2 * alter_y_nonlinear[0][i - 2]
    alter_y_linear[i] = y_out[i] - alter_y_nonlinear[0][i] + offset_factor
    result = my_recursive_least_squares(u, alter_y_linear, d, nb, na, P, Theta, Phi, i)
    a[:, i] = result[0][:, 0]
    b[:, i] = result[1][:, 0]
    coeff1 = a[:, i][0]
    coeff2 = a[:, i][1]
    coefficient = np.hstack((-a[:, i], b[:, i])).reshape(-1, 1).T
    print(f'i:{i} ', coefficient)
    P = result[2]
    Theta = result[3]
    Phi = result[4]
    K[:, i] = result[5][:, 0]

    if i > 4:
        y_n_1 = np.concatenate(([0], alter_y_nonlinear[0][:-1]))
        y_n_2 = np.concatenate(([0, 0], alter_y_nonlinear[0][:-2]))
        y_nonlinear_data = np.array([y_n_1, y_n_2])
        # coefficient[0][:2].reshape(-1, 2) @ y_nonlinear_data
        alter_y_nonlinear = y_out - coefficient @ u_train + offset_factor
        t_u_train = torch.tensor(u_train[:, 2:i].T, dtype=torch.float)
        t_u_val = torch.tensor(alter_y_nonlinear[0][2:i], dtype=torch.float).unsqueeze(1)
        if train_flag:
            train_model, loss_train = training_loop(
                n_epochs=256,
                optimizer=optimizer,
                model=train_model,
                loss_fn=nn.MSELoss(),
                t_u_train=t_u_train,
                t_u_val=t_u_val)
            if loss_train < 1e-4 and i > 200:
                torch.save(train_model.state_dict(), "model.pth")
                break
        else:
            # 加载已保存的状态字典
            train_model.load_state_dict(torch.load("model.pth"))
        nonlinear_train = torch.tensor(u_train, dtype=torch.float).T
        alter_y_nonlinear = train_model(nonlinear_train).detach().numpy().reshape(-1, 1).T

"""评估交替辨识算法"""
eval_nonlinear = torch.tensor(u_train, dtype=torch.float).T
eval_y_nonlinear = train_model(eval_nonlinear).detach().numpy().reshape(-1, 1).T
eval_u = np.zeros(N)
eval_y_line_out = np.zeros(N)
eval_y_out = np.zeros(N)
for k in range(2, N):
    eval_u[k] = 1 + 0.4 * np.sin(k / 5 * np.pi) + 0.5 * np.cos(k / 10 * np.pi)
    u_c_matrix[0] = u[k - 1]
    u_c_matrix[1] = u[k - 2]
    y_c_matrix[0] = y_out[k - 1]
    y_c_matrix[1] = y_out[k - 2]
    eval_y_line_out[k] = coefficient[0][:2] @ y_c_matrix + coefficient[0][2:] @ u_c_matrix
    eval_y_out[k] = eval_y_line_out[k] + eval_y_nonlinear[0][k]

plt.figure()
plt.plot(range(N), u, color='red', label='系统输入')
plt.plot(range(N), y_out, color='blue', label='系统输出')
plt.title("系统输入输出曲线图")
plt.legend(loc='upper right')
plt.xlabel("steps")
plt.ylabel("输入\输出")
plt.grid(True)

plt.figure()
plt.plot(range(N), y_out, color='red', label='ref_y')
plt.plot(range(N), eval_y_out, color='blue', label='eval_y')
plt.title("原始系统与辨识参数系统输出曲线对比图")
plt.legend(loc='upper right')
plt.xlabel("steps")
plt.ylabel("输出")
plt.grid(True)

plt.figure()
plt.plot(range(train_L), a[0, :train_L].T, color='b', label='a_1')
plt.plot(range(train_L), a[1, :train_L].T, color='g', label='a_2')
plt.plot(range(train_L), b[0, :train_L].T, color='r', label='b_0')
plt.plot(range(train_L), b[1, :train_L].T, color='m', label='b_1')
plt.plot(range(train_L), [A_coeff[1].T] * train_L, color='b', linestyle='--', label='ref_a_1')
plt.plot(range(train_L), [A_coeff[2].T] * train_L, color='g', linestyle='--', label='ref_a_2')
plt.plot(range(train_L), [B_coeff[0].T] * train_L, color='r', linestyle='--', label='ref_b_0')
plt.plot(range(train_L), [B_coeff[1].T] * train_L, color='m', linestyle='--', label='ref_b_1')
plt.title("A、B参数辨识曲线图")
plt.xlabel("steps")
plt.ylabel("辨识参数")
plt.grid(True)
plt.legend(loc='upper right')
plt.show()

递推最小二乘

import numpy as np


def recursive_least_squares(U, Y, d, nb, na, P, Theta, phi, n):
    nu = na + nb + 1  # Number of unknowns

    for j in range(1, nu + 1):
        if j <= na:
            if (n - j) <= 0:
                phi[n, j - 1] = 0
            else:
                phi[n, j - 1] = -Y[n - j]
        else:
            if (n - d - (j - (na + 1))) <= 0:
                phi[n, j - 1] = 0
            else:
                phi[n, j - 1] = U[n - d - (j - (na + 1))]

    print(Y[n], phi[n, :], U[n])
    K = np.array(np.dot(P, phi[n, :]) / (1 + np.dot(np.dot(phi[n, :], P), phi[n, :].T))).reshape(-1, 1)

    Theta = Theta + K * (Y[n] - np.dot(phi[n, :], Theta))

    P = np.eye(nu) - np.dot(K * phi[n, :], P)

    a = Theta[:na]
    b = Theta[na:]
    return a, b, P, Theta, phi, K


def my_recursive_least_squares(U, Y, d, nb, na, P, Theta, phi, n):
    nu = na + nb + 1  # Number of unknowns

    for j in range(1, nu + 1):
        if j <= na:
            if (n - j) <= 0:
                phi[n, j - 1] = 0
            else:
                phi[n, j - 1] = -Y[n - j]
        else:
            if (n - d - (j - (na + 1))) <= 0:
                phi[n, j - 1] = 0
            else:
                phi[n, j - 1] = U[n - d - (j - (na + 1))]

    phi_n = phi[n, :].reshape(1, -1)
    Y_n = Y[n]
    # 计算K
    temp = np.linalg.inv(1 + phi_n @ P @ phi_n.T)
    K = P @ phi_n.T @ temp

    # 更新Theta
    Theta = Theta + K * (Y_n - phi_n @ Theta)

    # 更新P
    # P = np.eye(nu, nu) - K @ phi_n @ P
    P = P - P @ phi[n, :].reshape(-1, 1) / (1 + phi[n, :] @ P @ phi[n, :].reshape(-1, 1)) @ phi[n, :].reshape(1, -1) @ P

    a = Theta[:na]
    b = Theta[na:]
    return a, b, P, Theta, phi, K

参考

[1]张亚军,柴天佑,杨杰.一类非线性离散时间动态系统的交替辨识算法及应用[J].自动化学报,2017,43(01):101-113.DOI:10.16383/j.aas.2017.c150759.

[2]杨杰,柴天佑,张亚军. 数据与模型驱动的电熔镁群炉需量预报方法[C]//.第27届中国过程控制会议（CPCC2016）摘要集.,2016:26.

[3]张亚军,柴天佑. 一类非线性离散时间动态系统的交替辨识算法[C]//.第26届中国过程控制会议（CPCC2015）论文集.,2015:128.

[4]张亚军. 基于未建模动态估计与补偿的非线性自适应切换控制方法的研究[D].东北大学,2014.

[5]Zhang Y, Chai T, Wang D. An alternating identification algorithm for a class of nonlinear dynamical systems[J]. IEEE transactions on neural networks and learning systems, 2016, 28(7): 1606-1617.

[6]侯媛彬, 汪梅, 王立琦. 系统辨识及其MATLAB仿真(附光盘)[M]. 科学出版社, 2004.

[7]夏天昌, 刘绍球, 朱可炎. 系统辨识:最小二乘法[M]. 清华大学出版社, 1983.