1.引言

看过UR机器人脚本手册的都应该知道有这样一个直线插补函数：

interpolate_pose(p_from, p_to, alpha);

参数：p_from表示初始pose，p_to表示目标pose，alpha通常为0-1之间的浮点数，如果alpha=0，则函数插值返回的pose是p_from；如果alpha=1，则函数插值返回的pose是p_to；如果alpha<0，则函数插值返回的pose是这条直线在p_from之前的部分；如果alpha>1，则函数插值返回的pose是这条直线在p_to之后的部分；
返回值：返回一个插值之后的pose；
这个函数在实际应用的过程中表现非常好，很少出现奇异点和不可达的点的问题。那么这个函数具体是如何实现的呢？
也许有人要说了，直线插补太简单了，不屑一顾。但是我看过许多国内机器人教材，很少能把机器人轨迹是如何生成的这一过程讲清楚，或者连一个简单的点到点直线插补全过程都写得含糊不清。
以前我也觉得这样简单的算法没什么好研究的，随便找本书或论文看看就知道了，但当我真正要在机器人上实现这一算法时，遇到了各种各样的问题，于是我就怀疑是否真的了解了机器人生成轨迹的方法，直到我看完这本书为止。

2.《Modern Robotics》

这本书的全称是《Modern Robotics - Mechanics, Planning, and Control》2016年出的机器人学方面的书。
这本书的第九章《Trajectory Generation》是我看过的十几本机器人学书籍里面写的最透彻的。
机器人轨迹的定义：机器人位置随时间变化的描述称为轨迹；
首先要明白两个概念：path和time scaling。
path表示一组路径的集合，也可以理解为一组机器人位置的集合；
time scaling表示一组时间序列，即什么时间机器人要到什么位置。
本章考虑了三种轨迹规划问题：点到点的直线轨迹；通过一系列时间和点的集合的问题；最短时间轨迹问题。
而本文只考虑点到点的直线轨迹问题。这个问题分为关节空间和工作空间两种，这两种在下文中都有详解。

3.Point-to-Point Trajectories

首先要区分路径（path）和时间尺度（time scaling）这两个概念。
路径用θ(s)表示，其中s就是时间尺度，有时s就是表示时间t，但将s与时间参数t分离是一种更有效的方式，本书就是这么做的。
时间尺度s(t)∈[0, 1]，t∈[0, T]，如果s=0，表示the start of the path，如果s=1时表示the end of the path。
将路径（path）和时间尺度（time scaling）合起来就是轨迹（trajectory）表示成θ(s(t))。轨迹的速度和加速度就可以表示为：

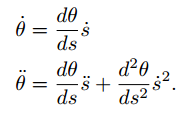
所以要想轨迹有较好的动态性能（即平滑的速度和加速度曲线），那么要保证θ(s)和s(t)都可以二次微分。

根据上面的分析，将轨迹分为θ(s)和s(t)，这样一来，路径就与时间进行了分离，分离的好处在于：如果想让轨迹是一条直线或圆弧，那么我们只需要考虑θ(s)函数的设计，而不用考虑时间问题；同理，如果我们想要得到梯形速度曲线或S形加速度曲线，那么也只用考虑s(t)函数，而不需要知道路径到底是直线还是圆弧；

所以，接下来的直线轨迹算法就分别以路径（path）和时间尺度（time scaling）进行。

4.Straight-Line Paths

如果是关节空间的直线插补，那么path就是：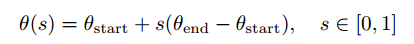

微分：

关节空间的直线插补，通常在工作空间不是直线运动。

如果是工作空间的直线插补，那么将上式的θ改成X表示工作空间的位置和姿态。
如果X是使用最小坐标集来表示工作空间的位置和姿态，这里的最小坐标集的意思是用最少的参数来表示位姿，如UR中使用的p[x, y, z, ax, ay, az]，那么工作空间的直线插补与上式一样：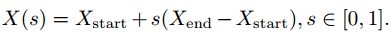

在上式的直线插补中，需要注意两个问题：

1. 如果路径会经过奇异点附近，那么几乎整个时间尺度上的所有路径的关节角速度都会变得非常大；
2. 因为机器人的工作空间可能不是凸的，所以有可能会出现Xstart和Xend都在工作空间内，但是中间点却不在工作空间内的情况；

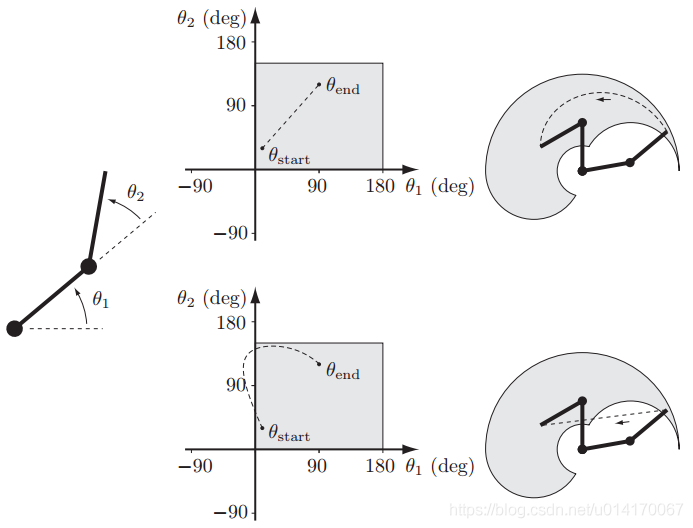
上图表示的是，在关节空间每个关节都进行直线插补，在工作空间的轨迹不是直线的情况；
下图表示的是，直线插补的起点和终点都在工作空间内，而插补出来的直线中间点不在工作空间内的情况；
上面的分析，是当X使用最小坐标集来表示工作空间的位置和姿态的情况。
如果X∈SE(3)的方式来表示机器人在工作空间的位姿，那么直线插补也要满足SE(3)的表示方法。这里的SE(3)的定义如下：
**定义1：**特殊欧几里得群（Special Euclidean Group）SE(3)，或者可以称为齐次变换矩阵，表示成：

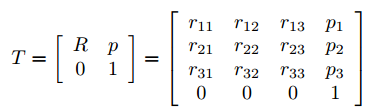
这里R∈SO(3)，p是列向量。（SO(3)见定义2）

通过螺旋运动的理论得到直线插补公式（具体怎么得到的这个公式请看《Modern Robotics - Mechanics, Planning, and Control》这本书）：

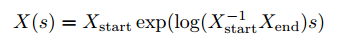
利用这个公式插补出来的直线，并不是一条直线，而是一条螺旋运动的轨迹。
通过将位置和姿态分离可以得到另外一个直线插补公式：

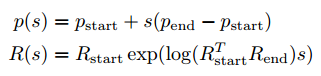
在这个公式里，R表示旋转变换矩阵，表示机器人在工作空间的姿态，p表示位置。通过这样位置和姿态分离之后，可以看出位置保持一条直线轨迹，而姿态以螺旋运动的方式变化。

以上两种公式，插补得到的直线轨迹区别如下图：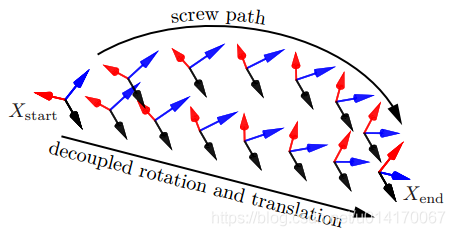

如图所示，上面一条轨迹没有分离位置和姿态（平移和旋转），实际得到的轨迹不是一条直线，而是一种螺旋运动曲线。而分离之后的轨迹在位置上是一条直线，姿态上以螺旋方式运动。

看了上面的公式，可能有人会觉得奇怪，怎么对矩阵进行对数、指数运算？
讨论这个问题之前，先插入两个定义：
**定义2：**特殊正交群（Special Orthogonal Group）SO(3)，也就是通常说的旋转变换矩阵，是一个33的实数矩阵R，满足：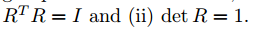

定义3：对于给定的向量：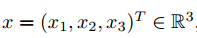

定义：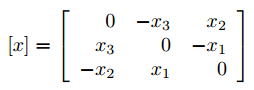

这里[x]是相对于x的33斜对称矩阵，对于所有这样的斜对称矩阵集合成为so(3)。

关于指数、对数的运算，这里只给出一个结论，至于为什么是这样的，就需要自己去看书了。
1.首先看矩阵的对数运算，如果R∈SO(3)，那么对R求对数得到：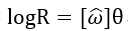

其中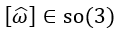

也就是说对R求对数就是将R转换成ω和θ的表示方式，如何得到ω和θ？方法如下：

2.再来看矩阵的指数运算：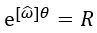

指数运算和对数运算是相反的过程，这里就表示将ω和θ转换成R，转换方法如下：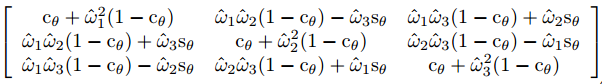

这里cθ和sθ分别表示cosθ和sinθ。

到这里，Straight-Line Paths的部分就结束了，接下来是Time Scaling。

5.Time Scaling a Straight-Line Path

这里只写三次多项式和梯形速度曲线两种，其他的都大同小异。
由上述轨迹的速度和加速度公式如下：

对于直线而言dθ/ds是常数，d²θ/ds²=0，所以直线轨迹的速度和加速度主要取决于ds/st和d²s/dt²。

1.三次多项式
对于时间尺度函数s(t)，三次多项式的形式为：

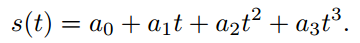
满足下列两个约束条件：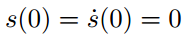

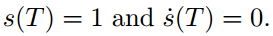
那么函数s(t)及其速度、加速度曲线如下：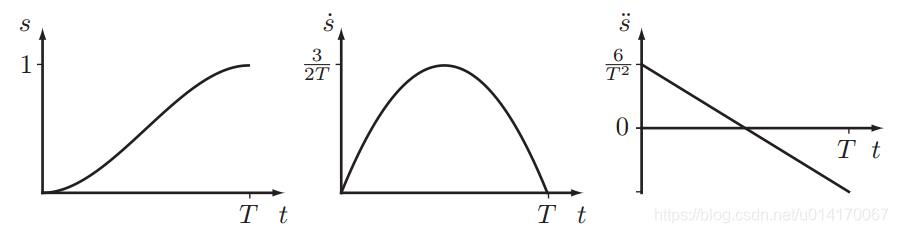

注意这里的s(t)∈[0,1]，将其代入上面的Path函数中，就能得到速度为二次曲线的直线插补轨迹；

2.梯形速度曲线
符合梯形速度曲线的公式如下：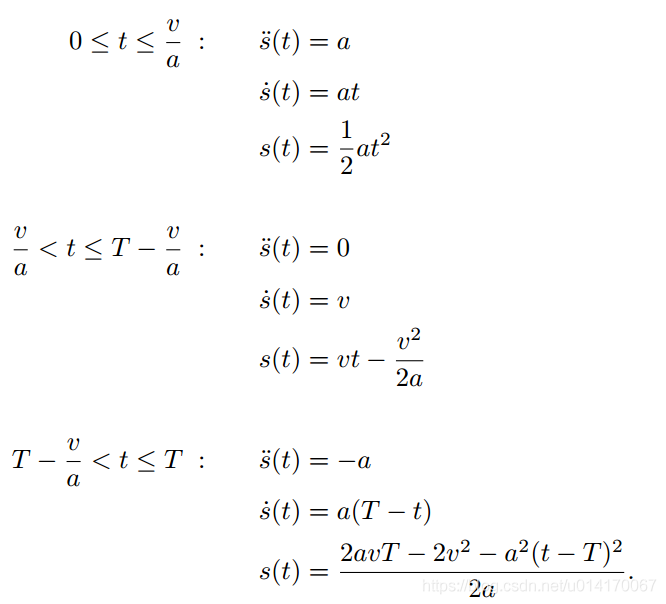

s(t)函数及其速度曲线如下图所示：

将s(t)代入到Path函数中，就可以得到速度满足梯形曲线要求的直线插补轨迹；

上面写了这么多，其实算法很简单，只是想说明一个思想，就是：轨迹(Trajectories)=路径(Path)+时间(Time Scaling)，将时间和路径分离开是这个思想的核心。明白了这个思想，看到其他更复杂的轨迹问题时，就会觉得简单明了。包括在代码实现的过程中，用这个思想封装API不论是自己还是让其他人调用起来也更加方便。