智能体位姿解算核心——欧拉角与四元数
描述
为这篇文章起了一个这样的标题,实属有感而发。位姿解算在机器人及自动驾驶中处处常见:传感器的姿态,车辆自身的姿态,物体姿态等。而这些姿态最重要的一种表现形式,就是欧拉角与四元数。借今天同事分享之机会,也重新给出一份专业详细的总结,为自己回顾也为未来做笔记。
当然了,这个知识并不高端,但理解得有多透,就因人而异了。看这篇文章,暂时请忘掉你的所有已知概念,这样理解起来会清晰得多
点、向量、坐标系
点
点,就是空间中的某点在某个坐标系下的表示,以三维空间为例,这个点就可以设为(a1,a2,a3),a1、a2、a3是纯数值
向量
向量,在空间中就是一个由起点指向终点的一个箭头,以三维空间为例,这个向量可以设为a
向量并不是点。只有在某个坐标系下,这个向量是由坐标系原点指向X点时,向量a的坐标值才可以理解为点
插一句:之前我写过很多文章,或多或少也体现了这一概念。我喜欢的说法是,某个点坐标值代表的向量,是它在这个坐标系下的表示)
坐标系
坐标系,由一组相互正交的坐标轴组成。(别和我说存在不正交的情况,确实有,正常工程里不会使用不正交的轴构成的坐标系,反正我是没用过)
我们让坐标系来串联一下点与向量的概念,举例:
三维空间中,我们可以令x轴的基为e_1(基,长度为1 ),y轴的基为e_2,z轴的基为e_3
那么向量a就可以写成
a =[e_1,e_2,e_3][a_1,a_2,a_3]^T=a_1e_1+a_2e_2+a_3e_3
右乘联体左乘基,再默背一下这最重要的口诀
向量的内积与外积
内积——点乘
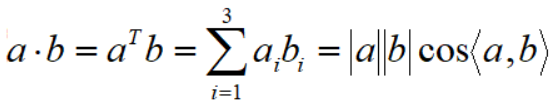
内积描述的是,向量b在向量a上投影的长度,与向量a的长度的乘积(也可以是a在b上的投影,与b的乘积,这两个结果相同),结果是一个数字
外积——叉乘
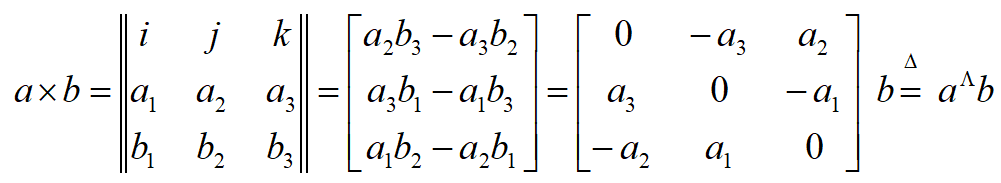
外积的结果是一个向量,它的方向垂直于这两个向量,大小等于|a||b|sin\left< a,b\right>
这里面要引入一个概念:反对称阵。它的特性是,对角线上元素为0,对角线两侧元素互为相反数。
反对称阵有很多不错的性质,在这里我们不介绍。简而言之,我们利用反对称阵来将向量外积转成矩阵乘法,这样比较方便
外积描述有几种解释
-
表示两个向量张成的平行四边行的有向面积
-
表示旋转
之前说过,外积的结果是一个向量,方向是垂直于a与b的。外积就是在空间中,向量a旋转到向量b的旋转轴,大小与两向量夹角相关。
旋转向量与旋转矩阵
旋转向量
三维空间中的从一个向量变换到另外一个向量,需要进行旋转和平移。我们需要对这种变换方式进行一种描述,让它可以把空间中任意的向量转换到另一个向量。最终我们发现:一个3维的向量表示旋转,1个三维的向量表示平移,就可以做到这点。这个表示旋转的3维向量,就是旋转向量。
旋转向量,其方向与旋转轴的方向一致,向量的长度(也就是大小)等于旋转角。
想象一下,空间中的任意两个坐标系,都可以通过一个旋转向量,变换到相同的姿态。再配合一个平移向量,两个坐标系就可以重合在一起啦!
旋转矩阵
定义了旋转向量固然好,但我们还需要定义一下旋转矩阵。
为什么,我们来描述一个这样的简单问题:坐标系下有一个点P或者说向量P,当我们利用一个旋转向量将向量P变换到了向量P’,点P’的坐标是什么呢?旋转向量的尺寸可以理解为(3,1),点坐标的尺寸也可以理解为(3,1),如果我们不定义一个尺寸为(3,3)的旋转矩阵,两个(3,1)的矩阵是计算不出新的点坐标(3,1)尺寸的。
从旋转向量到旋转矩阵的转换过程,可以被罗德里格斯公式(Rodrigues’s Formula)表明。

假设一个旋转轴为n(单位向量),角度为\theta的旋转,它的旋转向量就是 \theta n。利用角度值\theta和单位向量n,根据罗德里格斯公式我们可以计算得到旋转矩阵R。
从旋转矩阵中,我们也可以反推出旋转向量的信息。
旋转向量的角度值\theta
tr(R) = cos(\theta)tr(I)+(1-cos\theta)tr(nn^T)+sin\theta tr(n^{\wedge})
= 3cos\theta+ (1-cos\theta)
= 1+2cos\theta
公式中的计算依据tr(I)=3, tr(nn^T)=1, tr(n^{\wedge})=0
因此
\theta = arccos(\frac{tr(R)-1}{2})
旋转向量的旋转轴n
旋转轴上的向量在旋转后是不会发生变化的,也可以说旋转轴上的点坐标值旋转后是不会发生变化的,用矩阵乘法表示就是
Rn=n
实际上也可以写成Rn=1n
因此旋转轴n就是旋转矩阵R特征值为1时的特征向量。我们来列一下这个方程。
求解这个三元一次的方程组,得到xyz的值,再进行归一化,就是旋转轴了。
欧拉角
虽然旋转向量和旋转矩阵可以完成旋转这件事情,但是表现形式太抽象。因此欧拉角出现了。(以下只说明常用的欧拉角形式)
欧拉角有三个:
1.绕Z轴旋转,偏航角yaw
2.绕Y轴旋转,俯仰角pitch
3.绕X轴旋转,滚转角roll
这种定义方式被称为rpy,旋转顺序是ZYX,先绕Z轴旋转,再绕Y轴旋转,最后绕X轴旋转
绕Z轴旋转的旋转矩阵R_z是
绕Y轴旋转的旋转矩阵R_y是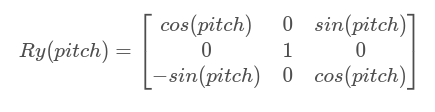
绕X轴旋转的旋转矩阵R_x是
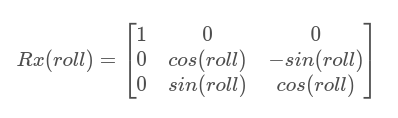
[r, p, y]^T这个3维的向量可以描述任意旋转,这三个欧拉角构成的旋转矩阵 R是
R = R_z R_y R_x
这里贴出两个C++代码
输入:3维平移向量+3个欧拉角,输出:齐次变换矩阵T
void T_get(double x, double y, double z, double rx, double ry, double rz){
rx = rx / 180 * PI;
ry = ry / 180 * PI;
rz = rz / 180 * PI;
Eigen::MatrixXd Rx(3, 3);
Eigen::MatrixXd Ry(3, 3);
Eigen::MatrixXd Rz(3, 3);
Rx << 1, 0, 0, 0, cos(rx), -sin(rx), 0, sin(rx), cos(rx);
Ry << cos(ry), 0, sin(ry), 0, 1, 0, -sin(ry), 0, cos(ry);
Rz << cos(rz), -sin(rz), 0, sin(rz), cos(rz), 0, 0, 0, 1;
Eigen::MatrixXd R(3, 3);
R = Rz * Ry * Rx;
Eigen::MatrixXd P(3, 1);
P << x, y, z;
T << R, P, MatrixXd::Zero(1, 3), MatrixXd::Identity(1,1);
//cout << T;
}
输入:齐次变换矩阵T,输出:3维平移向量+3个欧拉角
void get_pose_fromT(Eigen::MatrixXd T){
std::cout << T(0, 3) << std::endl;
std::cout << T(1, 3) << std::endl;
std::cout << T(2, 3) << std::endl;
std::cout << atan2(T(2, 1), T(2, 2)) /PI * 180 << std::endl;
std::cout << asin(-T(2, 0)) / PI * 180 << endl;
std::cout << atan2(T(1, 0), T(0, 0)) / PI * 180 << std::endl;
}
欧拉角的问题——万向锁(Gimbal Lock)问题
我们利用欧拉角,令坐标系依次绕Z、Y、X轴旋转时,当绕Y轴旋转(也就是俯仰角)±90°时,再执行的绕X轴旋转与第一次绕Z轴旋转,效果是一样的。再说简单些,当第二次旋转pitch是±90°时,第一次旋转的yaw和第三次旋转的roll效果相同。
万向锁可以搜一些动图方便理解。
简单来解释:为什么pitch会引发这个问题,又为什么是±90°。
我们依次绕Z、Y、X轴执行旋转,连续绕任意两轴旋转的效果(ZY与YX)一定是不同的(可以自行证明)。因此可以说,唯有ZX这两次旋转,可能由于中间这次绕Y轴的pitch角的大小,发生一些特殊现象。
而当$pitch$角为±90°时,RY这个旋转矩阵的值会是
我们可以计算一下RZ _ RY,再计算一下RY _ RX,你会发现二者的矩阵形式是相同的。
静态欧拉角与动态欧拉角
网上有些人会对欧拉角进行区分,并且说:静态欧拉角不存在万向锁,动态欧拉角才存在万向锁问题。首先说,这是一句正确的结论。
查阅了一下,对静态与动态进行一下我的说明:
- 静态:世界坐标系不动,物体来进行旋转
- 动态:物体在自身坐标系下进行旋转
显而易见的,静态不会出现万向锁问题,而动态会出现(自身坐标系都变了呀)。
实际上不用太在意这个静态或者动态的命名含义,我们只需要知道万向锁的产生原因,自然就知道什么情况会有问题了。不过既然提到这儿,还是多说一句。
一般的机器人和车辆,姿态变化是不会产生万向锁的。但是机械臂的关节运动,会出现万向锁问题。因此在机械臂的运动学建模分析及工程中,需要采用四元数来进行表示的。
总结
这篇文章对旋转向量、旋转矩阵、欧拉角等基本概念进行了分析。下一篇将介绍四元素的相关计算



评论(0)
您还未登录,请登录后发表或查看评论