Lyapunov稳定性理论我就先跳过了。有需要用到的时候，我会简单提一下。未来需要再读很多文献才能开始着手写nonlinear system。设计系列的文章我会先从SISO开始讲起，然后再往MIMO方面推广。这里先不涉及鲁棒控制和较多的最优控制的叙述，最优控制部分应该主要只讲LQR控制。LQG和EKF部分应该会在后面的文章中解释。离散控制的部分我会之后写离散的时候补充到后面，时变也暂时不考虑写进来，所以还是stick to LTI system吧。

本篇目录

1. 线性系统的反馈控制概述 Feedback Control of Linear System

2. 能控标准型 Controllability Canonical Form

3. 反馈控制律 - 极点配置 Feedback Control Law - Pole Placement

4. 不能控与“弱”能控性 Uncontrollability and weak controllability

经典控制理论中讨论了很多关于SISO系统的loop shaping的技巧，一般的设计方法可以分为根轨迹设计和频域法设计。以状态空间方程为基础的系统描述可以把系统内部机理表示出来，也可以将描述推广至非线性系统，也为几何概念的引入了便利[1]。

在接下来的文章中，我们从控制律设计，外部参考输入和观测器设计几个方面来介绍设计方法。这些设计是可以分开进行的，即“divide and conquer”（分而治之）。

1. 线性系统的反馈控制概述 Feedback Control of Linear System

反馈控制（Feedback Control）的使用主要目的还是抑制扰动问题。常见形式的反馈有：输出反馈（output feedback）和状态反馈（state feedback）。根据反馈控制律是否由一个动态过程决定的，还分为静态反馈（static feedback）和动态反馈（dynamic feedback）。我们平常总是用的  就是一种static feedback，而状态观测器用到的观测器方程就是一个动态过程，此时  中  就是由动态过程决定的，所以就是一种dynamic feedback。

我们一般说的反馈是指系统的输入将会受到输出的影响，相反，没有受到任何影响的系统，应当认为是开环的。不过反馈的概念也不一定要局限于影响输入，只要输出某种程度上返回来影响系统前向通路的任何一个环节，都可以形成一个拓扑结构上的闭环，可以认为也是反馈。

经典控制理论中采用的是输出反馈，直接把输出与参考输入  的误差信号 进行控制器处理，然后得到相应的输入  ，典型的就是PID控制器和lead-lag compensator。我们知道线性系统的输出  本质上也是由状态  构成的，如果我们认为系统的输出方程也是满足线性的，即系统可以写成  形式的状态空间方程，那么输出反馈也可以认为是一种状态反馈。但是由于输出函数  中  的行数往往少于系统维数，即输出的维度  一般要小于状态空间的维数  ，导致了  中包含的状态变量数要小于实际状态数，这样的反馈实际就造成了只有部分状态能够参与到反馈控制设计中。我们说输出反馈实际是一种部分状态反馈，它的控制效果与全状态反馈相比，由于缺少了几个状态变量，丢失了这些设计的自由度，一般是不如全状态反馈好的。

状态反馈，或者一般指的就是全状态反馈，是一种利用所有状态的信息构造反馈控制律的控制。理论上系统虽然是线性的，但是反馈规律的形式并一定是线性的。你可以构造非线性函数来做状态反馈也没有问题，难度在于证明其稳定性。稳定性证明方面，自然是线性的最容易了。所以使用一个线性的全状态反馈是比较保险的一种做法，其稳定性有诸多理论支持。上面说到的  就是由n个增益与状态乘积之和作为负反馈作用于系统的。这每一个增益  都是一种设计自由度，输出反馈中由于缺少了相应的  ，所以才造成实际效果有限，其本质就是无法自由配置闭环系统的特征值（eigenvalue），或者我们也叫系统的极点（pole）。

2. 能控标准型 Controllability Canonical Form

从传递函数到状态空间需要选取特定的实现。一个具体的实现可以是能控的，也可以是能观的。如果我们把一个传递函数按照能控标准型去实现，那么对应得到的状态空间方程和输出方程就是一个能控的系统。同理也可以放入能观标准型中去实现。但是无论是以何种方式去实现，如果传递函数本身是不存在零极点相消的，那么实现出来的状态空间是最小实现，必然是即能控又能观的。否则，以能控标准型实现，其能观性是不能保证的。所以无论是能控性还是能观性都是状态空间方程中系统体现出来的性质，是不能从传递函数中确定的[1]。关于能控标准型可以去这里复习一下：

三脚猫Frank：1. 状态空间与标准型 State Space and Canonical Form139 赞同 · 14 评论文章

在控制律设计中能控标准型表现出一定的优越性。不过由于目前这种控制设计基本都是靠MATLAB完成就行了，后期熟练使用MATLAB快速完成想法验证、设计和仿真才是比较重要的。

对于能控性，我们有一个定理说明了状态反馈与开环系统的关系[2]：

定理：线性状态反馈不改变线性系统(A,B,C)的能控性。

这个证明可以在[2]中找到，我就添加了两个字“线性”，因为它的证明是基于状态反馈是线性的前提下。在这里我们考虑的是添加了外部参考输入信号的反馈，  。所以形成的闭环系统的能控性依旧可以由  构成的能控性矩阵来衡量。既然闭环系统依旧是可控的，我们以后甚至还可以再增加outer loop，对  做第二次反馈设计。

然而对于能观性就不能断定了，由于线性状态反馈律的引入不会改变系统的零点[1]，那么改变对应系统的极点后，有可能会发生零极点对消，从而丢失能观性。

让我们来回顾一下SISO系统的能控标准型Controllable/Controllability Canonical Form:

我比较喜欢这种形式，  矩阵最后一行是传递函数的来自分母系数，  向量最后一行是  。在许多参考资料中也使用这种顺序定义状态变量间的积分关系。MATLAB与[1][2]是使用另外一种逆序定义状态变量的，所以得到的能控型  的第一行来自传递函数分母系数，  的第一行是  。两种形式本质上没有什么区别，就好像很多学术上的概念其实只是换了个名字，nothing fancy at all！

我们之前已经知道  ，那么如何得到非奇异变换矩阵让  成为  。

记  的每一行为  :

得到：

因为： 同理得到：

结合（3）与（4）得到

或者：

从而根据（3）能够得到  的每一行。

3. 反馈控制律 - 极点配置 Feedback Control Law - Pole Placement

学习经典控制理论的时候就知道了极点会影响系统的响应，尤其是稳定性。为了改善系统的响应和stabilize开环不稳定系统，我们希望能够自由配置极点。根轨迹设计法中我们可以选择感兴趣的参数，然后在复平面上根据需要寻找合适的极点位置以及阻尼大小，通过不断试错的方式去调整补偿器或者控制器的零极点得到一个满意的结果。在Bode plot的频域设计中，我们也可以根据loop shaping的技巧和经验来改变Bode曲线。但这些设计方法都有种经验主义的感觉，并不是精准且一步到位的。在状态反馈设计中配置极点，我们就可以做到这种相对精确的设计。

我们之前在能控性讨论中已经提过，一个系统（A,B）是能控的充要条件之一是矩阵 的特征值是可以自由配置的（complex eigenvalues are in conjugate pairs），只要选择一个合适的矩阵  [2][3]。换言之，闭环系统的极点在选择合适的反馈控制时是可以自由配置的，这给了我们设计系统很大程度的自由。但是有很多情况，对系统的所有极点进行重新配置是不必要的，因为首先这样做需要大量的状态信息，其次本身有些状态就是非常容易趋于稳定状态的，很快就会衰减，即状态的解本身就是稳定，这意味着没有必要花费控制力去对它们进行操作。另外有些时候可能不满足能控条件，那么对于不可控的部分状态，如果它是自身稳定的，我们依旧可以通过配置可控的极点来达到目标。因此除了controllability，我们又提出了一个新的概念，叫stabilizability[3]：

pair(A,B) is stabilizable if there exists a state feedback  such that the system is stable, i.e., (A-BF) is stable.
Matrix A is stable or Hurwitz if eigenvalue of A are all in the open left plane, i.e., 

所以只要不可控状态自身是stable的，我们就说系统是stabilizable的，这个性质比controllabe要弱，但很多系统只要满足这个性质就也已经足够了。由于通过Kalman Decomposition或者能控型分解可以将系统分解出能控的子系统，我们下面的讨论就只需要考虑完全能控的系统或者子系统就行了。

设计全状态反馈控制律中，我们把配置闭环系统极点的过程称之为极点配置（Pole Placement）。我们先讨论一下如何进行Pole Placement使得系统稳定，这是反馈控制律设计的重要前提。对于一个controllable piar（A,b）而言，我们就假设现在这个系统或者子系统有  维吧。暂时不考虑外部输入问题，我们设计全状态反馈控制律

其中的负号只是一个notation的问题，我们这里显示地写出来表示为一个negative feedback，  是一个增益矩阵(gain)，而  则是状态向量。显然（7）得到一个实数，然后将作用于被控制的plant。我们拿状态空间方程来看这个问题：

实际上我们得到了一个自治(autonoumous)闭环系统（因为我们没有加reference signal进来）。那么得到的闭环系统的稳定性就取决于矩阵  的特征值：当特征值的实部全部严格为负时，此系统是稳定的。那么Pole Placement的首要问题是要确保（7）使得（8）稳定。

我们看看如何计算  的特征值。我们知道这里的特征值实际就是传递函数分母的零点，系统的极点。我们用  代表系统的极点，得到特征方程：

我们知道配置好的闭环系统也有一个  的降幂排列特征方程方程，我们把它记为

（9）和（10）应该是同一个式子。这里就假设所有根，哪怕是重根都分开来写。这样一来，只要在（10）中选择期望的极点值，满足所有极点  ，再将（10）与（9）进行展开后的系数进行比较，就可以得到具体  矩阵中的值了。这样便完成了最基本的pole placement。当然这里我们没有考虑极点位置在左半复平面的选择问题，因为即便是稳定系统，其响应差异也很大，这个Selection of Pole Locations的问题，放到下一篇去讲。

使用Controllability Canonical Form: 上面的做法对于一个2维，3维的系统来讲还算简单[1, Example7.14, P466]，对于维数更高的系统而言，真是太费力了。那么我们可以借用Controllability Canonical Form来帮助我们更简单地完成pole placement。因为在能控标准型中，  的最后一行代表的是传递函数的分母表达式（最高次幂系数为1），所以我们只要按配置想法得到（10），并且展开得到降幂多项式后，其最终系数将会体现在  的最后一行。所以我们将会看到这样的闭环系统矩阵：(系数  是从0到  ，增益是从  到  )

这时候匹配系数就容易多了，假设配置好目标极点的（10）展开后的各项系数为  ，那么对应的  就是： 

所以pole placement的算法可以归结为: 将系统先转化为能控标准型，配置闭环极点，然后根据（12）得到增益矩阵  。最后要根据（7）和非奇异变换  ，得到原系统中的gain matrix：

Ackermann's formula: 一个名叫J.E. Ackermann的男人提出了一个便于计算的公式，称之为Ackermann's formula：

其中  是（10）中把  替换成原系统矩阵  ，（10）中的极点要配置好。这个公式对于计算维数小于10的SISO系统是不错的。在MATLAB中专门有一个函数叫acker，可以直接返回所需要的增益  。

Place in MATLAB： 对于更复杂的系统，MATLAB中提供了另外一个函数叫做place。看名字就知道是专门为了pole placement的。其相比较acker而言，主要是numerical stability更强。因为ackermann's formula采用了controllability matrix，而对于高维系统，其数值精度一般比较poor[1]。所以采用place是一种比较好的办法，可以参考MATLAB Docs查看place的算法。但是place不能将闭环极点分配到重根上面去，所以必须要求目标极点是distinct的。这个缺点，我们可以在配置时，令两个重根取值略微不同就可以避免。

4. 不能控与“弱”能控性 Uncontrollability and weak controllability

根据[1,p471]的说法，很少情况系统会出现完全不能控的情况，这个时候没有任何的反馈控制能够配置闭环系统的极点。所以从能控性角度上来讲，不能控的子系统是与系统脱节的。就好比，你父母一直唠叨你，你捂起耳朵不听一样，它们说的再有道理，你都听不进去。虽然我们能够通过计算能控性矩阵的秩来判别能控性，但是数学上和数值上的结果，需要practitioner有一个很好的interpretation。[1,p471]中讲到，一个控制工程师对于物理系统的理解是比所谓数学上的test更重要的。很多时候系统的有些模态只是在一定程度上是能控的（controllable to some degree），但是我们计算得到的能控性矩阵却可能是行满秩的。这样得到的能控性可能是很“弱”的，这意味着如果我们对SISO的能控性矩阵（此时为方阵）做特征值分解，其中有一些特征值非常小，几乎使得整个能控矩阵  是singular的。对于MIMO系统，我们可以采用Gramian的特征值分解，也可以采用  的SVD来看。

书中举例道： 飞行控制中，飞机的pitch motion是主要受到升降舵(elevator)影响，略微受到rolling motion的影响。而飞机的rolling motion主要是左右副翼(aileron)来控制的。

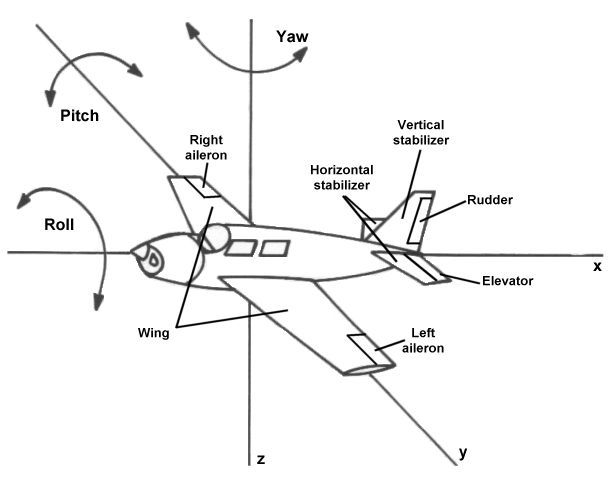
建模之后发现实际上pitch motion和rolling motion是耦合在一起的，也就是说rolling motion会影响到pitch motion，飞机机身翻滚时会略微影响飞机的仰角。那么我们是否可以人为aileron可以控制pitch呢？ 那显然是不对的，实际中没有人会那么做。但是如果去计算能控性矩阵，我们还是会得到  是满秩的，即便某些特征值非常接近0了。我们需要以工程实际的角度去解释这样的数值计算结果。

书中第二例子如下：

这个系统已经是能观标准型，所以  就是系统的一个零点。我们加入反馈控制之后得到闭环系统，从而计算出对应增益  。我们发现当开环零点  与开环极点(-3与-4)靠的很近时，系统的gain将会变得非常大，这个特点我们可以总结为[1,p473]：

If the controllability is almost lost, the control gains become very large. The system has to work harder and harder to achieve control as controllability slips away.

由于系统已经是能观型了，如果零极点靠得越近，能控程度就越弱，因为零极点相消会使得系统变得不能控。从增益变大我们可以看出来，能控程度的变弱，意味着控制力要愈加得大。这就好像把力作用在一个杠杆的短端，需要付出的力会很大。从对能控程度的分析可知，用aileron去控制pitch需要付出的control effort会非常巨大。

从这两个gain表达式中还可以看出，把闭环极点（  ）配置得离虚轴越远，即极点的实部越大，或者说  越大，就需要更大的增益（指绝对值）。观察式子我们发现  如果一直增大，增益就会跟着增长。我们可以粗略地把闭环带宽用  来估计，所以带宽越大，就需要更大的控制增益。这个结论我个人觉得还可以从数学角度——韦达定理来解释：因为闭环极点满足多项式方程，方程的系数和极点之间是存在关系的。显然极点和或者积的绝对值越大，那么系数就会越大，相应的增益就会变大。（在（12）中就很容易看出来）。

控制增益不能一味增大，驱动器都有自己的作用范围，大增益容易导致驱动器饱和。当然也很耗费能量，如果遇到扰动还容易产生巨大的信号偏差。

参考资料 Reference

[1] G.F. Franklin, J.D. Powell, A.Emami-Naeini, Feedback Control of Dynamic Systems, 7th Edition, 2014, Pearson

[2] 刘豹 唐万生，现代控制理论（第三版），2006， 机械工业出版社

[3] Robust and Optimal Control, Kemin Zhou with John C. Doyle and Keith Glover, Prentice Hall, Englewood Cliffs, NJ