步进电机加减速使用的场景有那些呢？为什么要使用加减速呢？

• 硬件驱动细分器与软件的细分参数或定时器分频参数设置不当时启动电机时，会遇见步进电机有啸叫声但是不会转动，这是因为软件产生脉冲的频率大于步进电机的启动频率，步进电机有一个很重要的技术参数：空载启动频率，也就是在没有负载的情况下能够正常启动的最大脉冲频率，如果脉冲频率大于该值，步进电机则不能够正常启动，发生丢步或者堵转的情况。
• 或者也可以理解为由于步进脉冲变化过快，转子由于惯性的作用跟不上电信号的变化。所以要使用加减速来解决启动频率低的问题，在启动时使用较低的脉冲频率，然后逐渐的加快频率。步进电机在开环控制的时候也需要有高精度，无积累误差等优点，被广泛应用于数控系统中，但是我们要实现步进电机的快速准确的定位，就要防止失步和过冲的现象发生，并以最快的速度到达指定的位置。

梯形加减速的介绍

为了使得不出现丢步或者超步现象并且提高效率，需要使得步进电机先以固定的加速度达到目标速度，然后以这个速度运行，快到达目标步数时再减到最低速；整个过程是一个梯形的模型。

步进电机因其无需反馈就能对位置和速度进行控制而在工业自动化设备中的应用极为广泛。例如这个装置使用步进电机实现物体 X 的移动，系统要求从 A 点出发，到 B点停止，移动的时间越短越好且系统稳定。

• 步进电机的特性，最大程度加大电机转速（提高脉冲频率），则到达 B 点的时间就越短，但是如果施加脉冲频率太高，超过了步进电机的最小启动频率，则会造成电机内部的反向电动势的阻尼作用，转子与定子之间的磁反应将跟随不上电信号的变化，导致堵转或者丢步，滑块连动都没动。
• 所以要求在电机启动时需要一个低速，但为了实现系统要求，在启动之后慢慢的升高速度，实现一个加速的过程，那如果在达到终点前一直在加速，就又有另外一个问题，到达终点时速度太快就会导致刹不住，出现过冲现象，为了防止这个现象我们需要在达到终点前的一段距离提前减速，使得滑块到达终点时速度刚好为 0，即从最高速度一直减至停止。如果在加速的过程中，从启动速度到目标速度的加减速是以一定的比例进行加速/减速。

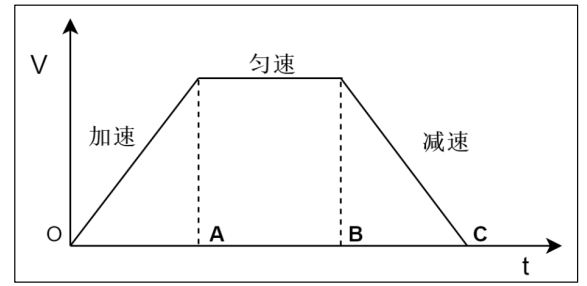
整个运动过程将滑块的速度变化一共分为三个阶段，OA 段其实就是滑块的加速部分、AB 则是匀速部分，BC 则是减速部分。因其图像呈现梯形，所以我们把这

种运动变化称之为梯形加减速。这种算法是一种在加速过程和减速过程中加速度不变的匀变速控制算法。

• OA 加速过程中，由低于步进电机的启动频率开始启动(模型中由 0 启动)，以固定的加速度增加速度到目标值
• AB匀速过程中，以最大速度匀速运动
• BC 减速部分中，以加速度不变的速度递减到 0

这种算法是一种在加速过程和减速过程中加速度不变的匀变速控制算法，由于速度变化的曲线有折点，所以在启动、停止、匀速段中很容易产生冲击和振动。

梯形加减速的原理

• 步进电机的转动需要控制器发送脉冲，如果控制器以恒定速度发送脉冲，那么步进电机就以恒定速度转动；如果控制器以加速度运动，那么步进电机就以加速度运动；所以只要改变脉冲的频率就可以改变速度的变化，也就是说调整脉冲之间的时间间隔就可以改变速度。
• 步进电机的速度由脉冲频率决定，在匀速运动的过程中，脉冲的频率是固定不变的，根据步进电机特性，每给一个脉冲，电机就会步进固定的距离（将角度转换为距离），知道了 A 点到 B 的距离，就可以计算出来步进电机需要走多少步，然后让控制器输出所需要且固定频率的脉冲就可以了。
• 在加减速段的过程中，速度是不断的改变的，通过需改变脉冲的频率，让电机在加速时给高频率的脉冲，减速时给低频率脉冲。

进行计算 — 确定未知量和已知量

• A.加速阶段时需要多少脉冲数 ====>使用 n1 进行表示

• B.减速阶段要步进多少脉冲数 ====>使用 n2 进行表示

• C.下一个变化的脉冲的周期是 ====>使用 T 进行表示

  因为要实现加减速效果，所以输送给电机的脉冲的周期是变化的，只要确定下一个脉冲的周期，并且确定加速阶段和减速阶段需要提供多少个脉冲，然后让控制器一个一个把脉冲送出去即可。

在进行加减速前需要确定的参数量有如下：

• A.电机需要步进的距离，使用 step 表示
• B.加速度大小，使用 accel 表示
• C.减速度大小，使用 decel 表示
• D.最大速度，决定电机匀速时的速度值，用 Max_ω 表示

这些参数在步进电机做加减速之前就要求用户来设置好，也就是我们的已知量。根据图可以知道，设置的参数不同，系统将有如下两种运动情况：

三角形运动变化的加减速阶段所需脉冲数

第一种设置情况：最大速度设置偏大，而加速度设置偏小，导致电机步进了很多步数依然没有达到最大速度，但此时距离终点 Step 可走的步速越来越少，再不减速将无法在终点时使速度降为 0。所以这种情况，其加速模型并不呈现梯形，加速不到最大速度将要被迫降速。

运动变化图形类似于三角形，上图全部有以下几个参数：

• Max_w：用户设置的最大速度

• accel：加速度大小

• decel ：减速度大小

• step ：总步数

  这些都是已知量，不需要求解，接着看下需要求解的变量

• max_s_lim：速度从 0 加速到 Max_w 所需要的步数，也就是与最大速度的交点；

• acc_lim ：加速度曲线与减速度曲线的相交点；
• decel：实际减速的步数；

此时 n1 = accel_lim，加速段延长线做数学模型，得出只要满足：acc_lim ≤ max_s_lim，运动变化状态就呈现三角形，首先我们通过求解 accel_lim 则可获知加速段的步数，不难看出，这里有一个等式条件：加速段的末速度 ω1 和开始减速的速度 ω2 是相等的。

此时的 t1 为加速段步进消耗的时间，t2 则是减速段的时间，从上图的模型中可知，梯形加减速运动规律符合物理学中匀加速运动，既然我们的疑问是关于加速过程中走过的距离问题，想必大家都已经想到了经典的位移公式，根据这个公式我们就获知时间 t，然后将时间 t转换为我们想要的步数。

位移 S 就是步进电机的步进距离，等于步距角（a）和脉冲个数(n)的乘积，在初速度为 0 则有以下公式，其中加速度 a 为角加速度W

将时间 t 转化为已知量可得

通过计算可得出想要求解的加速段的脉冲数 n1

因为 n1 和 n2 都是未知的，但是 n1+n2=step 是可知的

由上求解出了加速段脉冲数 n1，已知总的脉冲数 step 不变，则可知减速段 n2：

负号是因为减速阶段的运动方向和减速度的方向是相反的。

梯形运动变化的加减速阶段所需脉冲数

第二种设置情况：最大速度设置偏小，而加速度设置偏大，步进电机很快就加速到了设置的最大速度，距离设置的终点 max_w 还有剩余很长的步数可以走，此时，电机以最大速度匀速步进，直到满足减速条件才开始减速，并刚好使得速度到终点时降至 0。

由图得出只要满足：acc_lim >max_s_lim，运动变化状态就呈现梯形，那么此时加速段步数 n1=max_s_lim，由最大速度已知我们可以直接得到以下等式：

加速段的步数知道，也知道总步数，但是减速度段不单单只总步数减去加速度段，因为，中间需要一个匀速步进段，但是从图中可以看出，减速前的速度等于最大速度的条件是依然不变的，我们同样可以使用前面 的公式，求解减速段的步数。

• decel_val 是减速段的步数，而不是开始减速的步数，开始减速的步数等于总步数减掉减速段的步数（实际减速段步数为负值，所以直接将总步数与减速段步数相加即可）。
• 解决了加速和减速阶段时需要多少脉冲数的问题，接着还需要求出 accel_lim 的大小，以便在程序中比较 accel_lim 与 max_s_lim 的大小判断当前运动状态属于哪种情况。同样的交点满足速度相同所以。

后面还需要求解加减速段以及匀速段的脉冲间隔时间。

脉冲时间间隔的精确计算

步进电机速度的快慢是由脉冲频率的高低决定的，而脉冲频率的高低是由定时器的计算频率 ft 和计数值 cn 决定的，在计数频率不变的情况下，脉冲周期只由

定时器计数值决定，即在加速段/减速度的时候改变 cn 的值提升/降低步进电机速度，而在匀速时，保持最高速度对应下的 cn 值。

• t1 ：发送第二个脉冲的时刻
• t2 ：发送第三个脉冲的时刻
• &t ：两个脉冲之间的间隔时间
• c0 ：定时器从 t0~t1 时刻的定时器计数值
• c1 ：定时器从 t1~t2 时刻的定时器计数值
• tt : 定时器计数周期

例如 stm32 的高级定时器 8 为例，定时器 8 的时钟频率为 168MHZ，如果将分频值设置为83，那么定时器的计数频率则为: ft=168/(83+1)=2MHZ, 每过 1/ft=1/2Mhz=0.5us 则 cn 增加1，如果 Cn=10，则输出的脉冲周期则是 T=Cn*1/ft=5us，可知 Cn 越小，脉冲周期越小，电机速度越快，反之则越慢。

ft ：定时器的计数频率；

α ：步距角；

Spr ：步进电机旋转一圈脉冲数， 电机相关常数；

θ ：位置；

ω ：速度；

n ：脉冲数；

rad ：弧度单位，1rad/sec = 60/2π ≈ 9.55rpm

结合上述基本公式与下图的数学模型，可以看出在加速阶段，步进电机做的匀加速运动，并且初速度为 0，所以可得以下关系式:

S 表示位移；W表示加速度，tn 表示时间点，整理得:

• 可以将 tn 理解为某个时间点，结合基础公式

• 整理化简得

• 由此可知，当 n=0 时，代入上式，得到第 1 个脉冲的定时计数器值 C0 为:

• 最终计算：

从上面的式子可知，定时器计数值需要连续两次计算开方根才能得出结果，而我们面对的现实问题是：一般控制器的计算能力是有限的，连续

两次计算开方根在实时运动的过程中比较费时，因此这里还可做一些技巧性处理，帮控制器“减负”，但是带来的运算也会稍微复杂些，当然了，你也可以选择直接使用上面的式子。根据泰勒公式的一个特例麦克劳林公式：

• 可以对 Cn 进行一些转换，以使用简单的计算方法得出 Cn，下面是其推导过程：
  

• 进行处理

但是由于在化简时舍弃了无穷小余项，发现当 n=1 时有 0.4142 的偏差，我们可以将 C0乘一个系数 0.69 来解决这个误差。接着就是确定下一步定时器计数值的值。在加速和减速过程中的每一步新的时间间隔必须计算得出。而这个新的脉冲周期的确定需要使用前面费劲心思推导的下个脉冲周期：

• 使用 new_step_delay 进行表示下一个脉冲周期 Cn，上一个脉冲周期使用step_delay 进行表示，而 n 是记录第几个脉冲，使用 accel_count 表示

结果 new_step_delay 会包括一个系数和一个余数，为了提高精度余数保留并包含在下一次计算当中：

• 其中 rest 为余数，首次计算值为 0。new_ rest 就是保存除不尽的余数参与下一次计算。
• 求解的是加减速段的 c 值。还需要求解匀速段的 c 值，这个比较简单我们已知最大速度 w，且匀速段的脉冲频率不变

• 数值中有可能出现浮点数，而浮点数对我们的运算速度是有影响的，虽然 F4 集成硬件 FPU，但是为了兼容其他低性能的芯片，此算法会将系数放大，但是不影响最终运算结果
  

• 为了保持匀速段的 c 值大小不变，最大速度speed也会放大 10 倍（假设最大速度100，实际为 10，该值由用户设置），即得到 c 等于:
  

其他的数值求解同样使用了此方法来解决浮点数带来的影响