0. 简介
对于视觉里程计而言,在面对低纹理场景时,往往会出现退化的问题,究其原因是人造环境往往很难找到足够数量的点特征。而其他的几何视觉线索则是比较容易找到,在城市等场景中,通常表现出结构规律,如平行性或正交性,满足曼哈顿世界的假设。之前我们已经在《经典文献阅读之—PL-SLAM》文中介绍了点线SLAM的形式,相关的具体代码我们可以在Github上找到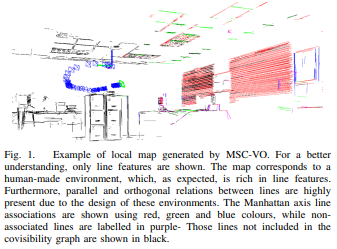
1. 文章贡献
在本文章中,我们则进一步介绍MSC-VO,一种基于rgb-d的视觉里程计方法,它结合了点和线特征,如果存在,可以利用这些结构规正和场景的曼哈顿轴。此外我们需要着重注意的是,这些结构约束最初被用来准确地估计提取的线的三维位置。这些约束还与估计的曼哈顿轴和点和线的重投影误差相结合,通过局部地图优化来细化相机姿态。这种组合使我们的方法即使在没有上述约束的情况下也能够运行,从而允许该方法在更广泛的场景中工作。具体的主要贡献如下
-
提出了一种鲁棒的针对低纹理环境的RGB-DVO框架,可以在场景中存在结构规律和MA对齐时提高姿态精度。否则,我们的解决方案仍然可以运行,这将在实验结果部分中显示。
-
一种基于场景中所呈现的结构信息的三维线端点计算方法。
-
一种精确、高效的三维局部地图优化策略,它将重投影误差与结构约束和MA对齐相结合。
-
一种新颖的MA初始化过程,通过在多图非线性最小二乘公式中使用多帧观测来改进传统采用的平均位移算法的估计。
2. 详细内容
MSC-VO建立在ORB-SLAM2[2]的跟踪和局部映射组件之上。因此,它包含两个并行运行的线程,如图2所示。其一开始结构和PL-SLAM类似,我们主要就介绍三维特征位置估计以及曼哈顿轴估计这两个部分。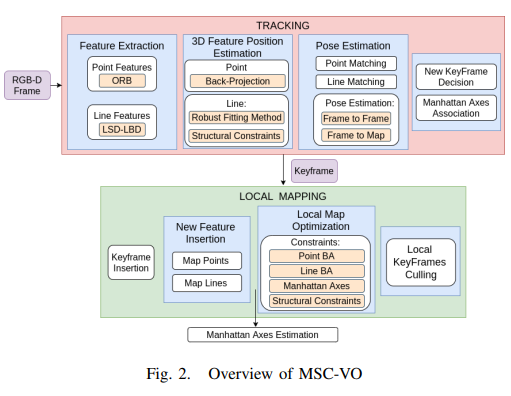
2.1 三维特征位置估计
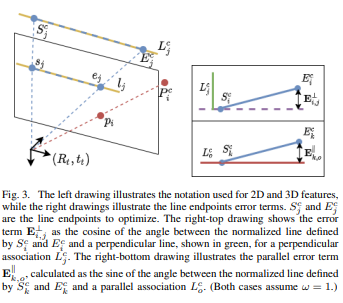
一旦检测到点和线并对其进行描述,就可以得到它们在摄像机坐标中的三维位置。将点p_i在I^d_t中的2D位置对应的值作为深度进行反向投影。由此得到的摄像机坐标中的3D位置表示为P^c_i。由于线条比点更容易受到深度不连续性和遮挡的影响,这个简单的过程可能会导致不准确的3D线条。为了降低这种影响,提出了一种鲁棒的两步法来计算三维直线端点。
首先,对于每个线段j,通过反向投影符合图像中直线的点子集,计算其端点的初始3D位置,记为{S^c_j, E^c_j},然后执行[14]中的鲁棒拟合步骤。三维归一化直线L^c_j的计算类似于等式1。然后,利用场景的结构约束来细化每条检测到的直线;我们首先把平行线和垂直线联系起来。为此,对于当前图像中检测到的每一对直线(L^c_m, L^c_n),我们通过点积计算两个方向向量之间夹角的余弦: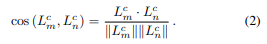
我们只选择那些余弦值接近0或1的线段对,(L^c_m, L^c_n)分别代表垂直线或平行线。对选定的直线对采用非线性优化方法优化其直线端点。为此,采用g2o[20]实现的Levenberg-Marquardt算法。形式上,我们定义直线L^c_m和L^c_n之间的方向差异d为: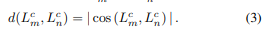
我们分别表示\mathbb{L}_⊥和\mathbb{L}_{||}为有效垂直线对和有效平行线对的集合。假设一对(L^c_m, L^c_n)∈\mathbb{L}_⊥,误差项\mathbb{L}_{m,n}^⊥为: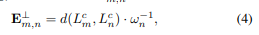
其中ω_n根据线段n的LSD算法返回的直线响应对误差项进行加权。同样,对于另一对(L^c_m, L^c_n)∈\mathbb{L}_{||},误差项\mathbb{L}_{m,n}^{||}定义如下: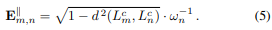
其中d(·,·)∈[0,1]:
我们将L定义为待优化的变量集,其中包括那些至少在\mathbb{L}_⊥或\mathbb{L}_{||}上有一个结构关联的直线,然后通过最小化以下成本函数来计算L的最佳直线端点: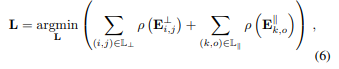
2.2 曼哈顿轴估计
如前所述,曼哈顿轴由三个正交的方向组成,在世界坐标中,它们代表了主要的场景方向。这些方向随着时间的推移保持固定,因此,它们的估计应该非常准确,以防止在优化步骤中出现偏差。为此,本文提出了一种由粗到细的MA估计策略,扩展了Kim等人[10]的工作。然后,通过考虑沿不同关键帧的多个线观测值来修正估计的MA。
首先,使用[10]中提出的基于Mean shift的方法,从第一个关键帧计算MA的第一次估计。在第一阶段中,涉及的特征只有网格上定义的一些点的线方向向量和表面法向量。使用改进的[22]算法计算法向量,该算法是基于积分图像计算法向量的,提高了计算速度。对下一个关键帧重复这个过程,直到得到有效的MA,尽管通常有噪声。
一旦局部映射包含足够数量的关键帧,用\mathcal{K}_M表示,在第二个MA细化阶段执行非线性优化程序,因此使用第一阶段计算的不准确的MA作为初始猜测。给定\mathcal{M}为MA的集合,定义\mathbb{V}^{MA_i}_k为关键帧k中观察到的与曼哈顿轴线MA_i相关联的地图线的集合,优化问题可表述为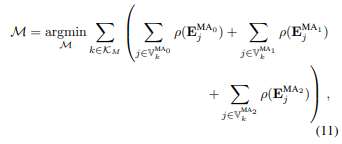
where the error term of a line j associated to the axis M_j ∈ \mathcal{M}is given b: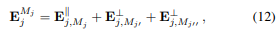
为M_{j’}和M_{j’’},另外两个MA与直线j不相关。最后,我们采用单值分解(SVD)来保证轴之间的正交性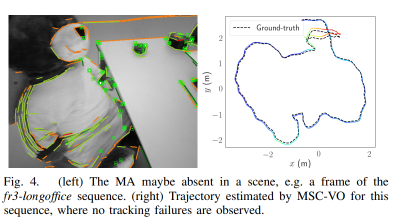






评论(0)
您还未登录,请登录后发表或查看评论